已知抛物线经过(-1,0)(0,-3)(2,-3)三点答案解析
科目:czsx
来源:
题型:
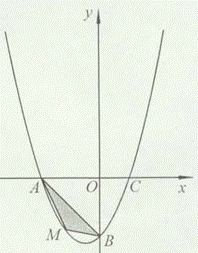
在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值;
(3)若点P是抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能使以点P、Q、B、0为顶点的四边形为平行四边形,直接 写出相应的点Q的坐标.
写出相应的点Q的坐标.
查看答案和解析>>
科目:czsx
来源:鼎尖助学系列—同步练习(数学 九年级下册)、求二次函数的函数关系式
题型:038
|
|
已知抛物线 经过(-1,0),(0,-3),(2,-3)三点. 经过(-1,0),(0,-3),(2,-3)三点.
| (1) |
|
(2) |
|
|
查看答案和解析>>
科目:czsx
来源:
题型:
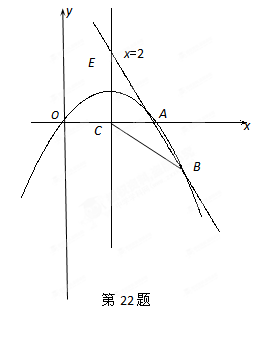
如图,已知抛物线经过原点

和
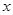
轴上另一点
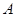
,它的对称轴
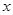
="2" 与
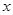
轴交于点

,直线
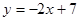
经过抛物线上一点

,且与直线
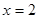
交于点

.

【小题1】求

的值及该抛物线的函数关系式;
【小题2】若点
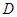
是
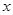
轴上一动点,当△
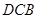
△∽△
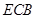
时,求点
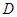
的坐标;
【小题3】若
是该抛物线上的一个动点,是否存在这样的点

,使得

,若存在,试求出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:2012届九年级上学期期末数学试卷
题型:解答题
查看答案和解析>>
科目:czsx
来源:
题型:
(14分)已知抛物线

经过A(3,0), B(4,1)两点,且与y轴交于点C.
(1)求抛物线

的函数关系式及点C的坐标;
(2)如图(1),连接AB,在题(1)中的抛物线上是否存在点P,使△PAB是以AB为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图(2),连接AC,E为线段AC上任意一点(不与A、C重合)经过A、E、O三点的圆交直线AB于点F,当△OEF的面积取得最小值时,求点E的坐标.

查看答案和解析>>
科目:czsx
来源:2011年初中毕业升学考试(贵州遵义卷)数学
题型:解答题
查看答案和解析>>
科目:czsx
来源:
题型:
已知抛物线 经过A(3,0), B(4,1)两点,且与y轴交于点C.
经过A(3,0), B(4,1)两点,且与y轴交于点C.
(1)求抛物线 的函数关系式及点C的坐标;
的函数关系式及点C的坐标;
(2)如图(1),连接AB,在题(1)中的抛物线上是否存在点P,使△PAB是以AB为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图(2),连接AC,E为线段AC上任意一点(不与A、C重合)经过A、E、O三点的圆交直线AB于点F,当△OEF的面积取得最小值时,求点E的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
已知抛物线经过点A(0,4)、B(1,4)、C(3,2),与x轴正半轴交
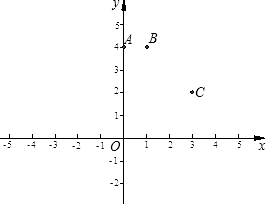
于点D.
(1)求此抛物线的解析式及点D的坐标;
(2)在x轴上求一点E,使得△BCE是以BC为底边的等腰三角形;
(3)在(2)的条件下,过线段ED上动点P作直线PF∥BC,与BE、CE分别交于点F、G,将△EFG沿FG翻折得到△E′FG.设P(x,0),△E′FG与四边形FGCB重叠部分的面积为S,求S与x的函数关系式及自变量x的取值范围.
查看答案和解析>>
科目:czsx
来源:
题型:
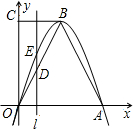
如图,已知抛物线经过坐标原点O和x轴上另一点E,顶点M的坐标为 (2,4);矩形ABCD的顶点A与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3.
(1)直接写出该抛物线所对应的函数关系式;
(2)将矩形ABCD以每秒1个单位长度的速度从图1所示的位置沿x轴的正方向匀速平行移动,同时一动点P也以每秒1个单位长度的速度从A点出发沿射线AB匀速移动,设它们运动的时间为t秒(t>0),直线AB与该抛物线的交点为N(如图2所示).
①填空:当0<t≤3时,PN=
-t2+3t
-t2+3t
.(用含t的代数式表示);
②在运动的过程中,以P、N、C、D为顶点的四边形能否成为平行四边形?若能,请求出此时t的值,若不能,请说明理由.
③设以P、N、C、D为顶点的多边形面积为S,试问S是否存在最小值?为什么?
查看答案和解析>>
科目:czsx
来源:
题型:
根据下列条件,求二次函数的关系式
(1)已知抛物线的顶点在(1,-2),且过点(2,3);
(2)已知抛物线经过(2,0)、(0,-2)和(-2,3)三点.
查看答案和解析>>
科目:czsx
来源:
题型:
已知抛物线经过点A(1,0)、B(2,-3)、C(0,4)三点.
(1)求此抛物线的解析式;
(2)如果点D在这条抛物线上,点D关于这条抛物线对称轴的对称点是点C,求点D的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
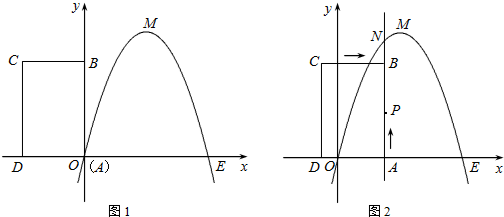
如图l,已知抛物线经过坐标原点O和x轴上另一点D,顶点的坐标为(2,4).直角三角形ABC的顶点A与点O重合,AC,AB分别在x轴,y轴上,且AC=3,AB=4.
(1)直线BC的解析式为
;
(2)求该抛物线的函数关系式;
(3)将直角三角形ABC以每秒1个单位长度的速度从图1所示的位置沿x轴的正方向匀速平行移动,同时一动点P也以相同的速度从点A出发向B匀速移动,设它们运动的时间为t秒(0≤t≤2),AB边与该抛物线的交点为Q(如图2所示).
①设△CPQ的面积为S,试问S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由;
②直接写出直线BC与抛物线有唯一的公共点时t的值.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,已知抛物线经过坐标原点O及A(
-2,0),其顶点为B(m,3),C是A
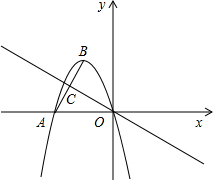
B中点,点E是直线OC上的一个动点 (点E与点O不重合),点D在y轴上,且EO=ED.
(1)求此抛物线及直线OC的解析式;
(2)当点E运动到抛物线上时,求BD的长;
(3)连接AD,当点E运动到何处时,△AED的面积为
?请直接写出此时E点的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
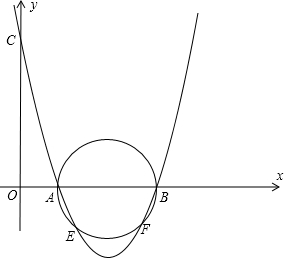
已知抛物线经过点A(1,0)、B(3,0)、C(0,3),以AB为直径画圆.
(1)求此抛物线的解析式;
(2)求该圆与抛物线交点(除A、B外)坐标;
(3)以AB的中点O′为圆心画圆,该圆的半径r与此抛物线的交点个数有何关系(直接写出结论)
查看答案和解析>>
科目:czsx
来源:
题型:
如图甲所示,已知抛物线经过原点O和x轴上另一点E,顶点M的坐标为(2,4);
(1)求抛物线函数关系式;
(2)矩形ABCD的顶点A与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3,将矩形ABCD以每秒1个单位长度的速度从图甲所示的位置沿x轴的正方向匀速平移,同时一动点P也以相同的速度从点A出发向B匀速移动,设它们运动的时间为t秒(0≤t≤3),直线AB与该抛物线的交点为N(如图乙所示).
①当
t=时,判断点P是否在直线ME上,并说明理由;
②设以P、N、C、D为顶点的多边形面积为S,试问S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由;
③现将甲图中的抛物线向右平移m(m>0)个单位,所得抛物线与x轴交于G、F两点,与原抛物线交于点Q,设△FGQ的面积为S,求S关于m的函关系式.

查看答案和解析>>
科目:czsx
来源:
题型:
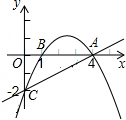
(2012•天水)如图,已知抛物线经过A(4,0),B(1,0),C(0,-2)三点.
(1)求该抛物线的解析式;
(2)在直线AC上方的该抛物线上是否存在一点D,使得△DCA的面积最大?若存在,求出点D的坐标及△DCA面积的最大值;若不存在,请说明理由.
(3)P是直线x=1右侧的该抛物线上一动点,过P作PM⊥x轴,垂足为M,是否存在P点,使得以A、P、M为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
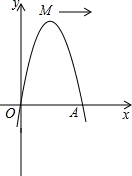
如图,已知抛物线经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),
(1)求该抛物线的解析式;
(2)现将它向右平移m(m>0)个单位,所得抛物线与x轴交于C、D两点,与原抛物线交于点P,△CDP的面积为S,求S关于m的关系式;
(3)当m=2时,点Q为平移后的抛物线的一动点,是否存在这样的⊙Q,使得⊙Q与两坐标轴都相切?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
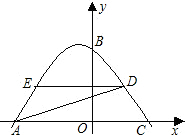
如图,已知抛物线经过点A(-3,0),B(0,3),C(2,0)三点.
(1)求此抛物线的解析式;
(2)如果点D(1,m)在这条抛物线上,求m的值的点D关于这条抛物线对称轴的对称点E的坐标,并求出tan∠ADE的值.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,直角梯形OABC中,∠COA=90°,BC∥OA,OA=6,BC=3,AB=
3,已知抛物线经过O、A、B
三点.
(1)求抛物线的解析式;
(2)平行与y轴的直线l从点O向终点A匀速运动,速度是每秒1个单位长,运动时间为t秒.直线l交折线段OBA于点D,交抛物线于点E.问:当t为何值时,线段DE有最大值?最大值是多少?
(3)探索:坐标平面内是否存在一点F,使得以C、B、D、F为顶点的四边形是菱形?如果存在,请直接写出点F的坐标;如果不存在,请说明理由.
查看答案和解析>>

![]() 写出相应的点Q的坐标.
写出相应的点Q的坐标.
 和
和 轴上另一点
轴上另一点 ,它的对称轴
,它的对称轴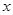 ="2" 与
="2" 与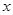 轴交于点
轴交于点 ,直线
,直线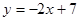 经过抛物线上一点
经过抛物线上一点 ,且与直线
,且与直线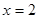 交于点
交于点 .
.
 的值及该抛物线的函数关系式;
的值及该抛物线的函数关系式;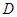 是
是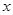 轴上一动点,当△
轴上一动点,当△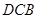 △∽△
△∽△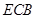 时,求点
时,求点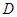 的坐标;
的坐标;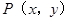 是该抛物线上的一个动点,是否存在这样的点
是该抛物线上的一个动点,是否存在这样的点 ,使得
,使得 ,若存在,试求出所有符合条件的点P的坐标;若不存在,请说明理由.
,若存在,试求出所有符合条件的点P的坐标;若不存在,请说明理由.  和
和 轴上另一点
轴上另一点 ,它的对称轴
,它的对称轴 =2 与
=2 与 轴交于点
轴交于点 ,直线
,直线 经过抛物线上一点
经过抛物线上一点 ,且与直线
,且与直线 交于点
交于点 .
.
 的值及该抛物线的函数关系式;
的值及该抛物线的函数关系式; 是
是 轴上一动点,当△
轴上一动点,当△ △∽△
△∽△ 时,求点
时,求点 的坐标;
的坐标; 是该抛物线上的一个动点,是否存在这样的点
是该抛物线上的一个动点,是否存在这样的点 ,使得
,使得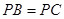 ,若存在,试求出所有符合条件的点P的坐标;若不存在,请说明理由.
,若存在,试求出所有符合条件的点P的坐标;若不存在,请说明理由. 经过A(3,0), B(4,1)两点,且与y轴交于点C.
经过A(3,0), B(4,1)两点,且与y轴交于点C. 的函数关系式及点C的坐标;
的函数关系式及点C的坐标;
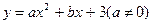 经过A(3,0), B(4,1)两点,且与y轴交于点C.
经过A(3,0), B(4,1)两点,且与y轴交于点C.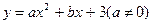 的函数关系式及点C的坐标;
的函数关系式及点C的坐标;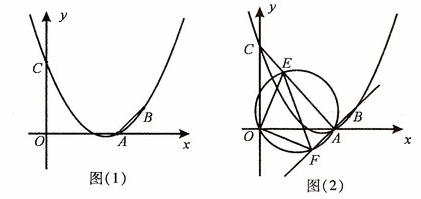
![]() 经过A(3,0), B(4,1)两点,且与y轴交于点C.
经过A(3,0), B(4,1)两点,且与y轴交于点C.![]() 的函数关系式及点C的坐标;
的函数关系式及点C的坐标;
![]() 和
和![]() 轴上另一点
轴上另一点![]() ,它的对称轴
,它的对称轴![]() =2 与
=2 与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 经过抛物线上一点
经过抛物线上一点![]() ,且与直线
,且与直线![]() 交于点
交于点![]() .
.
![]() 的值及该抛物线的函数关系式;
的值及该抛物线的函数关系式;![]() 是
是![]() 轴上一动点,当△
轴上一动点,当△![]() △∽△
△∽△![]() 时,求点
时,求点![]() 的坐标;
的坐标;![]() 是该抛物线上的一个动点,是否存在这样的点
是该抛物线上的一个动点,是否存在这样的点![]() ,使得
,使得![]() ,若存在,试求出所有符合条件的点P的坐标;若不存在,请说明理由.
,若存在,试求出所有符合条件的点P的坐标;若不存在,请说明理由. 于点D.
于点D.

 B中点,点E是直线OC上的一个动点 (点E与点O不重合),点D在y轴上,且EO=ED.
B中点,点E是直线OC上的一个动点 (点E与点O不重合),点D在y轴上,且EO=ED. 已知抛物线经过点A(1,0)、B(3,0)、C(0,3),以AB为直径画圆.
已知抛物线经过点A(1,0)、B(3,0)、C(0,3),以AB为直径画圆.
 (2012•天水)如图,已知抛物线经过A(4,0),B(1,0),C(0,-2)三点.
(2012•天水)如图,已知抛物线经过A(4,0),B(1,0),C(0,-2)三点.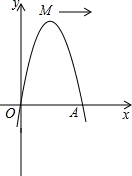 如图,已知抛物线经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),
如图,已知抛物线经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2), 如图,已知抛物线经过点A(-3,0),B(0,3),C(2,0)三点.
如图,已知抛物线经过点A(-3,0),B(0,3),C(2,0)三点. 三点.
三点.