在Rt△ABC中，∠ACB=90°，BC答案解析

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

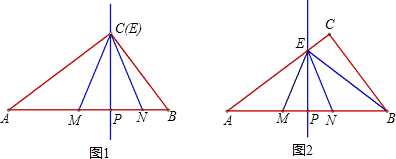
在Rt△ABC中，∠ACB=90°，BC=a，AC=b，AB=c，斜边上的高CD=h，△ABE是以AB为斜边的等腰直角三角形，连接CE．
①以a+b，c+h，h的长为边的三角形是直角三角形．
②以

1

a

，

1

b

，

1

h

的长为边的三角形是直角三角形．
③AC²-BC²=AD²-DB²．④CA+CB=

2

AE．其中正确的是（　　）

A．①②③

B．②③④

C．①②④

D．①②③④

科目：czsx 来源： 题型：

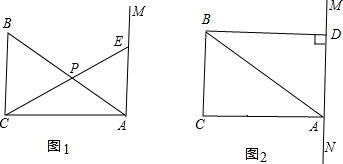
（2012•昌平区二模）在Rt△ABC中，∠ACB=90°，BC=4．过点A作AE⊥AB且AB=AE，过点E分别作EF⊥AC，ED⊥BC，分别交AC和BC的延长线与点F，D．若FC=5，求四边形ABDE的周长．

科目：czsx 来源： 题型：

在Rt△ABC中，∠ACB=90°，BC=30，AB=50．点P是AB边上任意一点，直线PE⊥AB，与边AC或BC相交于E．点M在线段AP上，点N在线段BP上，EM=EN，sin∠EMP=

12

13

．
（1）如图1，当点E与点C重合时，求CM的长；
（2）如图2，当点E在边AC上时，点E不与点A、C重合，设AP=x，BN=y，求y关于x的函数关系式，并写出函数的定义域；
（3）若△AME∽△ENB（△AME的顶点A、M、E分别与△ENB的顶点E、N、B对应），求AP的长．

科目：czsx 来源： 题型：

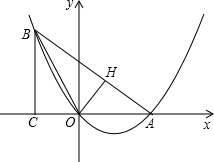
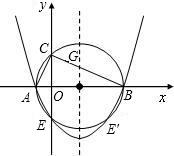如图，在Rt△ABC中，∠ACB=90°，BC＞AC，以斜边AB所在直线为x轴，以斜边AB上的高所在直线为y轴，建立直角坐标系，若OA²+OB²=17，且线段OA、OB的长度是关于x的一元二次方程x²-mx+2（m-3）=0的两个根．
（1）求C点的坐标；
（2）以斜边AB为直径作圆与y轴交于另一点E，求过A、B、E三点的抛物线的解析式，并画出此抛物线的草图；
（3）在抛物线上是否存在点P，使△ABP与△ABC全等？若存在，求出符合条件的P点的坐标；若不存在，说明理由．

科目：czsx 来源： 题型：

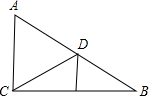如图，在Rt△ABC中，∠ACB=90°，BC的垂直平分线交斜边AB于D，AB=12 cm，AC=6 cm，则图中等于60°的角共有（　　）

A、2个

B、3个

C、4个

D、5个

科目：czsx 来源： 题型：

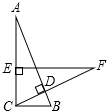如图，在Rt△ABC中，∠ACB=90°，BC=3cm，CD⊥AB，在AC上取一点E使EC=BC，过点E作EF⊥AC交CD的延长线于点F，若EF=5cm，则AE=

2

2

．

科目：czsx 来源： 题型：

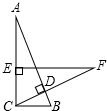如图，在Rt△ABC中，∠ACB=90°，BC=4cm，CD⊥AB，在AC上取一点E，使EC=BC，过点E作EF⊥AC交CD的延长线于点F，若EF=10cm，则AE=

6

6

cm．

科目：czsx 来源： 题型：

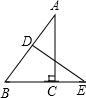如图，在Rt△ABC中，∠ACB=90°，BC=3，AC=4，AB的垂直平分线DE交BC的延长线于点E，则CE的长为（　　）

A、 3 2

B、 7 6

C、 25 6

D、2

科目：czsx 来源： 题型：

科目：czsx 来源： 题型：

（2013•武汉模拟）如图，已知在Rt△ABC中，∠ACB=90°，BC＞AC，⊙O为△ABC的外接圆，以点C为圆心，BC长为半径作弧交CA的延长线于点D，交⊙O于点E，连接BE、DE．
（l）求∠DEB的度数；
（2）若直线DE交⊙0于点F，判断点F在半圆AB上的位置，并证明你的结论．

科目：czsx 来源： 题型：

运动探究
如图，在Rt△ABC中，∠ACB=90°，BC=AC=10，CP⊥AB于P，顶点C从O点出发沿x轴正方向移动，顶点A随之从y轴正半轴上一点移动到点O为止．
（1）若点P的坐标为（m，n），求证：m=n；
（2）若OC=6，求点P的坐标；
（3）填空：在点C移动的过程中，点P也随之移动，则点P运动的总路径长为

 

．

科目：czsx 来源： 题型：

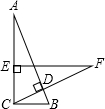（2012•临沂）在Rt△ABC中，∠ACB=90°，BC=2cm，CD⊥AB，在AC上取一点E，使EC=BC，过点E作EF⊥AC交CD的延长线于点F，若EF=5cm，则AE=

3

3

cm．

科目：czsx 来源： 题型：

14、如图，在Rt△ABC中，∠ACB=90°，BC=6，正方形ABDE的面积为100，则正方形ACFG的面积为（　　）

A、64

B、36

C、82

D、49

科目：czsx 来源： 题型：

已知：在Rt△ABC中，∠ACB=90°，BC=6，AC=8，过点A作直线MN⊥AC，点E是直线MN上的一个动点，
（1）如图1，如果点E是射线AM上的一个动点（不与点A重合），连接CE交AB于点P．若AE为x，AP为y，求y关于x的函数解析式，并写出它的定义域；
（2）在射线AM上是否存在一点E，使以点E、A、P组成的三角形与△ABC相似，若存在求AE的长，若不存在，请说明理由；
（3）如图2，过点B作BD⊥MN，垂足为D，以点C为圆心，若以AC为半径的⊙C与以ED为半径的⊙E相切，求⊙E的半径．

科目：czsx 来源： 题型：

如图，在Rt△ABC中，∠ACB=90°，BC=8

2

，cosA=

1

3

，则斜边AB上中线CD的长为

 

．

科目：czsx 来源： 题型：

（2013•平遥县模拟）已知：如图，在Rt△ABC中，∠ACB=90°，BC=3，tan∠BAC=

3

4

，将∠ABC对折，使点C的对应点H恰好落在直线AB上，折痕交AC于点O，以点O为坐标原点，AC所在直线为x轴建立平面直角坐标系．
（1）求过A、B、O三点的抛物线解析式；
（2）若在线段AB上有一动点P，过P点作x轴的垂线，交抛物线于M，设PM的长度等于d，试探究d有无最大值？如果有，请求出最大值，如果没有，请说明理由．
（3）若在抛物线上有一点E，在对称轴上有一点F，且以O、A、E、F为顶点的四边形为平行四边形，试求出点E的坐标．

科目：czsx 来源： 题型：

19、如图，在Rt△ABC中，∠ACB=90°，BC=2，正方形ABDE的面积为10，则正方形ACFG的面积为

6

．

科目：czsx 来源： 题型：

如图在Rt△ABC中，∠ACB=90°，BC=3，AB=5，则下列结论正确的是（　　）

A．sinA= 4 5

B．tanA= 3 5

C．cosB= 4 5

D．tanB= 4 3

科目：czsx 来源： 题型：

如图，在Rt△ABC中，∠ACB=90°，BC=3，AC=4，AB的垂直平分线DE交BC的延长线于点E，则CE的长为

 

．