精英家教网 >
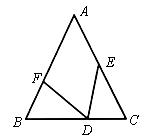
试题搜索列表 >如图,在等腰△ABC中,AB=AC,∠ABC=a,在四边形BDEC中,DB=DE,∠BDE=2a
如图,在等腰△ABC中,AB=AC,∠ABC=a,在四边形BDEC中,DB=DE,∠BDE=2a答案解析
科目:czsx
来源:
题型:
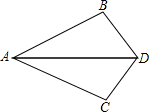
如图,△ABD和△ACD中,AB=AC,当添加条件
DB=CD
DB=CD
时,就可得到△ABD≌△ACD(写出一个条件即可)
查看答案和解析>>
科目:czsx
来源:
题型:
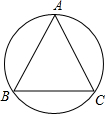
如图,已知⊙O中,
=,∠C=65°,则∠A=
50
50
度.
查看答案和解析>>
科目:czsx
来源:2011年广州市八年级第一学期期中考试数学卷
题型:填空题
如图,△ABD和△ACD中,AB=AC,当添加条件________时,就可得到△ABD≌△ACD(写出一个条件即可)

查看答案和解析>>
科目:czsx
来源:
题型:
如图,△ABD和△ACD中,AB=AC,当添加条件________时,就可得到△ABD≌△ACD(写出一个条件即可)

查看答案和解析>>
科目:czsx
来源:
题型:
如图,△ABD和△ACD中,AB=AC,当添加条件________时,就可得到△ABD≌△ACD(写出一个条件即可)

查看答案和解析>>
科目:czsx
来源:2011年广州市第三十七中学八年级第一学期期中考试数学卷
题型:填空题
如图,△ABD和△ACD中,AB=AC,当添加条件________时,就可得到△ABD≌△ACD(写出一个条件即可)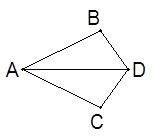
查看答案和解析>>
科目:czsx
来源:不详
题型:填空题
如图,△ABD和△ACD中,AB=AC,当添加条件______时,就可得到△ABD≌△ACD(写出一个条件即可)
查看答案和解析>>
科目:czsx
来源:
题型:
如图(1), 中,AB=AC,AD是中线,P是AD上一点,过C作CF//AB,连结BP并延长,交AC于点E,交CF于点F。
中,AB=AC,AD是中线,P是AD上一点,过C作CF//AB,连结BP并延长,交AC于点E,交CF于点F。
求证: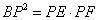
查看答案和解析>>
科目:czsx
来源:数学教研室
题型:044
如图,已知DABC中,AB=AC,ÐA=120°,AB的垂直平分线交AB于E,交BC于F,求证CF=2BF。
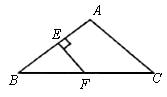
查看答案和解析>>
科目:czsx
来源:数学教研室
题型:013
如图,已知DABC中,AB=AC,CD=BF,BD=EC,则ÐEDF等于( )
A.90°-ÐA
B.45°-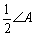
C.180°-ÐA
D.90°-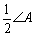
查看答案和解析>>
科目:czsx
来源:河南省同步题
题型:解答题
如图,平面直角坐标系中,AB⊥AC,求点B的坐标。
查看答案和解析>>
科目:czsx
来源:数学教研室
题型:013
如图,已知DABC中,AB=AC,BC=BD,AD=DE=EB,则ÐA等于( )
A.30° B.36°
C.45° D.54°

查看答案和解析>>
科目:czsx
来源:2011年北京市通州区中考二模数学试卷
题型:单选题
查看答案和解析>>
科目:czsx
来源:
题型:
如图2,已知
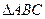
中,AB=AC=2,

,
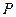
是
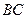
边上一个动点,过点
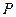
作

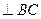
,交
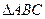
其他边于点

.若设

为

,
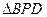
的面积为
,则
与

之间的函数关系的图象大致是( )

查看答案和解析>>
科目:czsx
来源:
题型:
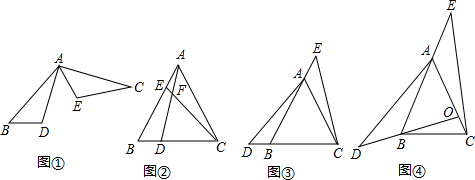
问题情境:如图①,在△ABD与△CAE中,BD=AE,∠DBA=∠EAC,AB=AC,易证:△ABD≌△CAE.(不需要证明)
特例探究:如图②,在等边△ABC中,点D、E分别在边BC、AB上,且BD=AE,AD与CE交于点F.求证:△ABD≌△CAE.
归纳证明:如图③,在等边△ABC中,点D、E分别在边CB、BA的延长线上,且BD=AE.△ABD与△CAE是否全等?如果全等,请证明;如果不全等,请说明理由.
拓展应用:如图④,在等腰三角形中,AB=AC,点O是AB边的垂直平分线与AC的交点,点D、E分别在OB、BA的延长线上.若BD=AE,∠BAC=50°,∠AEC=32°,求∠BAD的度数.
查看答案和解析>>
科目:czsx
来源:
题型:
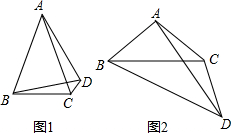
如图1,等腰△ABC,AB=AC,∠A<60°,D为△ABC外部一点,在AB的右侧作∠ABD=60°,且∠ADB=∠ACB
(1)探究线段AB、CD和BD的数量关系;
(2)若将“∠A<60°”改为“∠A>60°”,(1)中的结论是否还成立?若成立,给出证明;若不成立,给出正确的结论,并简要说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
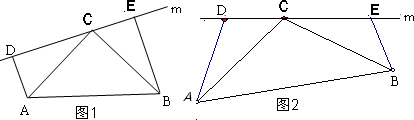
28、(1)如图1,等腰直角△ABC的直角顶点C在直线m上,AD⊥m,BE⊥m,垂足分别为D、E.试说明:
①△ADC≌△CEB;
②AD+BE=DE;
(2)习题演变:如图2,等腰△ABC中,AC=CB,若顶点C在直线m上,点D、E也在直线m上,若∠ACB=∠ADC=∠CEB=110°,题(1)的结论AD+BE=DE还成立吗?并说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:阅读理解
(2012•西城区二模)阅读下列材料
小华在学习中发现如下结论:
如图1,点A,A
1,A
2在直线l上,当直线l∥BC时,
S△ABC=S△A1BC=S△A2BC.
请你参考小华的学习经验画图(保留画图痕迹):
(1)如图2,已知△ABC,画出一个等腰△DBC,使其面积与△ABC面积相等;
(2)如图3,已知△ABC,画出两个Rt△DBC,使其面积与△ABC面积相等(要求:所画的两个三角形不全等);
(3)如图4,已知等腰△ABC中,AB=AC,画出一个四边形ABDE,使其面积与△ABC面积相等,且一组对边DE=AB,另一组对边BD≠AE,对角∠E=∠B.

查看答案和解析>>
科目:czsx
来源:
题型:
(2012•延庆县一模)如图1,已知:已知:等边△ABC,点D是边BC上一点(点D不与点B、点C重合),求证:BD+DC>AD.
下面的证法供你参考:
把△ACD绕点A顺时针旋转60°得到△ABE,连接ED,则有△ACD≌△ABE,DC=EB,∵AD=AE,∠DAE=60°,
∴△ADE是等边三角形,∴AD=DE.在△DBE中,BD+EB>DE,即:BD+DC>AD
实践探索:
(1)请你仿照上面的思路,探索解决下面的问题:
如图3,点D是等腰直角三角形△ABC边上的点(点D不与B、C重合).求证:BD+DC>
AD.
(2)如果点D运动到等腰直角三角形△ABC外或内时,BD、DC和AD之间又存在怎样的数量关系?直接写出结论.
创新应用:
(3)已知:如图4,等腰△ABC中,AB=AC,且∠BAC=α(α为钝角),D是等腰△ABC外一点,且∠BDC+∠BAC=180°,BD、DC与AD之间存在怎样的数量关系?写出你的猜想,并证明.

查看答案和解析>>
科目:czsx
来源:
题型:
已知:如图13,等腰△ABC中,底边BC=12,高AD=6.
(1)在△ABC内作矩形EFGH,使F、G在BC上,E、H分别在AB、AC上,且长是宽的2倍.求矩形EFGH的面积.
(2)在(1)的基础上,再作第二个矩形,使其两个顶点在EH上,另外两个顶点分别在AB、AC上,且长是宽的2倍.则第二个矩形的面积为 ;
(3)在(2)的基础上,再作第三个矩形,使其两个顶点在第二个矩形的边上,另外两个顶点分别在AB、AC上,且长是宽的2倍.则第三个矩形的面积为 ;
(4)按照这样的方式做下去,根据上述计算猜想第四个矩形的面积为 ;第 个矩形的面积为 .
个矩形的面积为 .
查看答案和解析>>



![]()
![]()

 中,AB=AC=2,
中,AB=AC=2, ,
, 是
是 边上一个动点,过点
边上一个动点,过点 作
作
 ,交
,交 其他边于点
其他边于点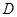 .若设
.若设 为
为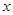 ,
,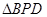 的面积为
的面积为 ,则
,则 与
与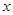 之间的函数关系的图象大致是( )
之间的函数关系的图象大致是( )

 如图1,等腰△ABC,AB=AC,∠A<60°,D为△ABC外部一点,在AB的右侧作∠ABD=60°,且∠ADB=∠ACB
如图1,等腰△ABC,AB=AC,∠A<60°,D为△ABC外部一点,在AB的右侧作∠ABD=60°,且∠ADB=∠ACB


![]() 个矩形的面积为 .
个矩形的面积为 .