
科目:gzsx 来源:101网校同步练习 高一数学 苏教版(新课标·2004年初审) 苏教版 题型:044
已知点A(4,0),B(4,4),C(2,6),试用向量方法求直线AC和OB(O为坐标原点)交点P的坐标.
科目:gzsx 来源:学习周报 数学 北师大课标高一版(必修4) 2009-2010学年 第46期 总202期 北师大课标版 题型:044
已知点A(4,0),B(4,4),C(2,6),试用向量方法求直线AC和OB(O为坐标原点)的交点P的坐标.
科目:gzsx 来源: 题型:
 已知点A(0,1),B,C是x轴上两点,且|BC|=6(B在C的左侧).设△ABC的外接圆的圆心为M.
已知点A(0,1),B,C是x轴上两点,且|BC|=6(B在C的左侧).设△ABC的外接圆的圆心为M.| AB |
| AC |
| l1 |
| l2 |
| l2 |
| l1 |
科目:gzsx 来源:必修二训练数学北师版 北师版 题型:044
已知点P(2,0),直线l的方程为2x-y-2=0.
(1)如果直线l1过点P,且l1∥l,求直线l1的方程;
(2)如果直线l2过点P,且l2⊥l,求直线l2的方程.
科目:gzsx 来源:101网校同步练习 高一数学 苏教版(新课标·2004年初审) 苏教版 题型:044
已知点P(2,0),直线l的方程2x-y-2=0
(1)如果直线l1过点P,且l1∥l,求直线l1的方程.
(2)如果直线l2过点P,且l2⊥l,求直线l2的方程.
科目:gzsx 来源:2010年山东省泰安四中高考数学模拟试卷(理科)(解析版) 题型:选择题
 的交点中,距离最近的两点间的距离为
的交点中,距离最近的两点间的距离为 ,那么此函数的最小正周期是( )
,那么此函数的最小正周期是( )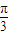
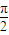
科目:gzsx 来源:2010年上海市宝山区高考数学一模试卷(文理合卷)(解析版) 题型:解答题
 的左右焦点,其渐近线为
的左右焦点,其渐近线为 ,且右顶点到左焦点的距离为3.
,且右顶点到左焦点的距离为3. ,且
,且 ,求k的值;
,求k的值; ,求m的值及△ABC的面积S△ABC.
,求m的值及△ABC的面积S△ABC.科目:gzsx 来源:2013届山西省晋商四校高二下学期联考理科数学试卷(解析版) 题型:解答题
已知直三棱柱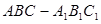 中,
中, 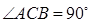 ,
,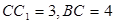 ,
,
 是
是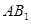 和
和 的交点, 若
的交点, 若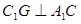 .
.
(1)求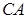 的长; (2)求点
的长; (2)求点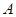 到平面
到平面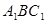 的距离;
的距离;
(3)求二面角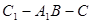 的平面角的正弦值的大小.
的平面角的正弦值的大小.
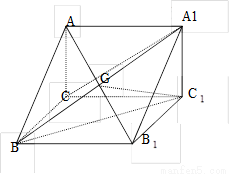
【解析】本试题主要考查了距离和角的求解运用。第一问中,利用ACC A
A 为正方形,
为正方形,  AC=3
AC=3
第二问中,利用面BB C
C C内作CD
C内作CD BC
BC ,
则CD就是点C平面A
,
则CD就是点C平面A BC
BC 的距离CD=
的距离CD=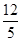 ,第三问中,利用三垂线定理作二面角的平面角,然后利用直角三角形求解得到其正弦值为
,第三问中,利用三垂线定理作二面角的平面角,然后利用直角三角形求解得到其正弦值为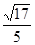
解法一: (1)连AC 交A
交A C于E, 易证ACC
C于E, 易证ACC A
A 为正方形,
为正方形,  AC=3
…………… 5分
AC=3
…………… 5分
(2)在面BB C
C C内作CD
C内作CD BC
BC ,
则CD就是点C平面A
,
则CD就是点C平面A BC
BC 的距离CD=
的距离CD=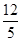 … 8分
… 8分
(3) 易得AC
 面A
面A CB,
过E作EH
CB,
过E作EH A
A B于H, 连HC
B于H, 连HC ,
则HC
,
则HC
 A
A B
B

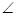 C
C HE为二面角C
HE为二面角C -A
-A B-C的平面角. ……… 9分
B-C的平面角. ……… 9分
 sin
sin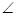 C
C HE=
HE=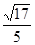
 二面角C
二面角C -A
-A B-C的平面角的正弦大小为
B-C的平面角的正弦大小为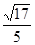 ……… 12分
……… 12分
解法二: (1)分别以直线C B、CC
B、CC 、C
、C A为x、y为轴建立空间直角坐标系, 设|CA|=h, 则C
A为x、y为轴建立空间直角坐标系, 设|CA|=h, 则C (0,
0, 0), B
(0,
0, 0), B (4,
0, 0), B(4, -3, 0), C(0, -3,
0), A
(4,
0, 0), B(4, -3, 0), C(0, -3,
0), A (0,
0, h), A(0, -3, h), G(2, -
(0,
0, h), A(0, -3, h), G(2, -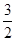 , -
, -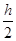 ) ……………………… 3分
) ……………………… 3分

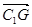 =(2, -
=(2, -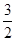 , -
, -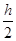 ),
), 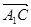 =(0,
-3, -h) ……… 4分
=(0,
-3, -h) ……… 4分

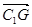 ·
·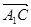 =0,
=0,
 h=3
h=3
(2)设平面A BC
BC 得法向量
得法向量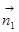 =(a, b, c),则可求得
=(a, b, c),则可求得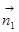 =(3, 4, 0) (令a=3)
=(3, 4, 0) (令a=3)
 点A到平面A
点A到平面A BC
BC 的距离为H=|
的距离为H=|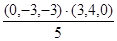 |=
|=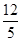 ……… 8分
……… 8分
(3) 设平面A BC的法向量为
BC的法向量为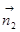 =(x, y, z),则可求得
=(x, y, z),则可求得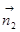 =(0, 1, 1) (令z=1)
=(0, 1, 1) (令z=1)
 二面角C
二面角C -A
-A B-C的大小
B-C的大小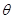 满足cos
满足cos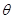 =
=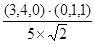 =
=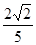 ………
11分
………
11分
 二面角C
二面角C -A
-A B-C的平面角的正弦大小为
B-C的平面角的正弦大小为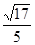
科目:gzsx 来源: 题型:
 (1)如图,向量
(1)如图,向量| OA |
| OB |
| OA/ |
| OB/ |
| π |
| 3 |
|
| π |
| 3 |
| 1 |
| 2 |
科目:gzsx 来源: 题型:
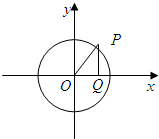 已知点P是圆x2+y2=1上的一个动点,过点P作PQ⊥x轴于点Q,设
已知点P是圆x2+y2=1上的一个动点,过点P作PQ⊥x轴于点Q,设| OM |
| OP |
| OQ |
| OP |
| OM |
科目:gzsx 来源: 题型:
科目:gzsx 来源: 题型:
|
| α |
|
|
|
科目:gzsx 来源:2014届山东省临沂市高三9月月考文科数学试卷(解析版) 题型:解答题
已知A、B、C是直线 上的不同三点,O是
上的不同三点,O是 外一点,向量
外一点,向量 满足
满足 ,记
,记 ;
;
(1)求函数 的解析式;
的解析式;
(2)求函数 的单调区间.
的单调区间.
科目:gzsx 来源: 题型:
已知点F(1,0),直线l:x=2.设动点P到直线l的距离为d,且|PF|=![]() d,
d,![]() ≤d≤
≤d≤![]() .
.
(1)求动点P的轨迹方程;
(2)若![]() ·
·![]() =
=![]() ,求向量
,求向量![]() 与
与![]() 的夹角.
的夹角.