科目:czsx
来源:
题型:

如图,校园要建苗圃,其形状如直角梯形,有两边借用夹角为135°的两面墙,另外两边是总长为30m的铁栅栏.
(1)求梯形的面积y与高x的表达式;
(2)求x的取值范围.
查看答案和解析>>
科目:czsx
来源:中学学习一本通 数学 九年级下册 北师大课标
题型:044
|
|
如图所示,校园要建苗圃,其形状为直角梯形,其两边借用夹角为 的两面墙.另外两边是总长为30米的竹篱笆. 的两面墙.另外两边是总长为30米的竹篱笆.
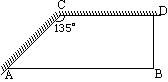
| (1) |
|
(2) |
|
|
查看答案和解析>>
科目:czsx
来源:
题型:解答题
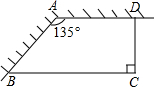 如图,校园要建苗圃,其形状如直角梯形,有两边借用夹角为135°的两面墙,另外两边是总长为30m的铁栅栏.
如图,校园要建苗圃,其形状如直角梯形,有两边借用夹角为135°的两面墙,另外两边是总长为30m的铁栅栏.
(1)求梯形的面积y与高x的表达式;
(2)求x的取值范围.
查看答案和解析>>
科目:czsx
来源:
题型:
22、(1)若此长方形空地长为am,宽为bm,中间建一条形状如图宽1米的小路(如图1),其余空地植草皮.则空地植草皮面积为
b(a-1)
m
2.
(2)如图2,若有一长80米,宽60米的广场,要按图中位置修筑两条路,要使其余空地面积为4524米
2,则路宽是
2
米.

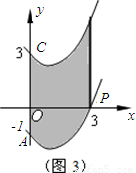
(3)如图3,抛物线y=ax
2+bx+c(a>0)经过点P(3,0),与y轴相交于点A(0,-1),若抛物线向上运动,使点A运动至点C(0,3),在运动过程中保持形状不变,则抛物线中的AP段运动所形成的图形(阴影部分)面积是多少?

查看答案和解析>>
科目:czsx
来源:同步轻松练习 九年级 数学 上
题型:044
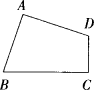
有一批铁板的边角料,其形状如图所示,其中∠A=∠C=90°,AB=AD.
现要把每块这样的材料都加工成正方形,并且希望材料的利用率尽量高,怎样加工最好呢?
查看答案和解析>>
科目:czsx
来源:新课程 新理念 新思维·同步练习篇·数学 九年级下册(苏教版) 苏教版
题型:044
公园要建圆形的喷水池(如图1),在水池中央垂直于水面安装一个柱子OA,O恰好在水面中心,OA=1.25 m,由柱子顶端A处的喷头向外喷水,水流在各个方面沿形状相同的抛物线路线落下.为使水流形状较为漂亮,要求设计成水流在与OA距离1 m处达到距水面最大高度2.25 m.如果不计其他因素,那么水池半径至少要多少米,才能使喷出的水流不致落到水池外?

查看答案和解析>>
科目:czsx
来源:
题型:解答题
(1)若此长方形空地长为am,宽为bm,中间建一条形状如图宽1米的小路(如图1),其余空地植草皮.则空地植草皮面积为________m2.
(2)如图2,若有一长80米,宽60米的广场,要按图中位置修筑两条路,要使其余空地面积为4524米2,则路宽是________米.

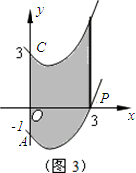
(3)如图3,抛物线y=ax2+bx+c(a>0)经过点P(3,0),与y轴相交于点A(0,-1),若抛物线向上运动,使点A运动至点C(0,3),在运动过程中保持形状不变,则抛物线中的AP段运动所形成的图形(阴影部分)面积是多少?
查看答案和解析>>
科目:czsx
来源:2011年4月浙江省某区中考数学二模试卷(解析版)
题型:解答题
(1)若此长方形空地长为am,宽为bm,中间建一条形状如图宽1米的小路(如图1),其余空地植草皮.则空地植草皮面积为______m
2.
(2)如图2,若有一长80米,宽60米的广场,要按图中位置修筑两条路,要使其余空地面积为4524米
2,则路宽是______米.

(3)如图3,抛物线y=ax
2+bx+c(a>0)经过点P(3,0),与y轴相交于点A(0,-1),若抛物线向上运动,使点A运动至点C(0,3),在运动过程中保持形状不变,则抛物线中的AP段运动所形成的图形(阴影部分)面积是多少?
查看答案和解析>>
科目:czsx
来源:
题型:044
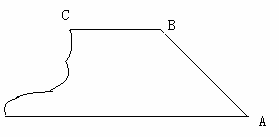
有一横断面为等腰梯形的防洪坝被洪水冲掉一角后其形状如下图所示.请用想法利用所学的知识设计一种方案将这个等腰梯形补全(不写作法)
查看答案和解析>>
科目:czsx
来源:测试专家八年级数学下册 第19章 四边形、19.3 梯形(二)
题型:068
|
|
有一横断面为等腰梯形ABCD的防洪堤被洪水冲掉一角后其形状如图所示:

| (1) |
|
请用尺规作图的方法将这个等腰梯形补充完整(不写作法,保留作图痕迹)
|
|
(2) |
|
已知AB=6,BC=4,∠A=60°,求这个横断面的面积.
|
|
|
查看答案和解析>>
科目:czsx
来源:
题型:

某小区要建一个花圃,花圃形状是由一个直角三角形和一个半圆形构成.具体的边长如图所示,其中直角三角形斜边AC为5米,直角边AB为b米,直角边BC为2a米.
(1)用含a,b的整式表示这个花圃的面积.
(2)若要从B到D修一条小路,小路BD与直角三角形斜边AC垂直,请用含a,b的整式表示小路BD的长.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,某学校校园内有一块形状为直角梯形的空地ABCD,其中AB∥DC,∠B=90°,AB=100m,
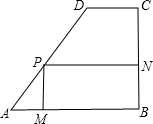
BC=80m,CD=40m,现计划在上面建设一个面积为S的矩形综合楼PMBN,其中点P在线段AD上,且PM的长至少为36m.
(1)求边AD的长;
(2)设PA=x(m),求S关于x的函数关系式,并指出自变量x的取值范围;
(3)若S=3300m
2,求PA的长.(精确到0.1m)
查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(50):2.3 二次函数的应用(解析版)
题型:解答题
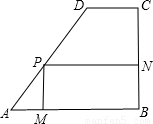
如图,某学校校园内有一块形状为直角梯形的空地ABCD,其中AB∥DC,∠B=90°,AB=100m,BC=80m,CD=40m,现计划在上面建设一个面积为S的矩形综合楼PMBN,其中点P在线段AD上,且PM的长至少为36m.
(1)求边AD的长;
(2)设PA=x(m),求S关于x的函数关系式,并指出自变量x的取值范围;
(3)若S=3300m
2,求PA的长.(精确到0.1m)
查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(47):2.4 二次函数的应用(解析版)
题型:解答题
如图,某学校校园内有一块形状为直角梯形的空地ABCD,其中AB∥DC,∠B=90°,AB=100m,BC=80m,CD=40m,现计划在上面建设一个面积为S的矩形综合楼PMBN,其中点P在线段AD上,且PM的长至少为36m.
(1)求边AD的长;
(2)设PA=x(m),求S关于x的函数关系式,并指出自变量x的取值范围;
(3)若S=3300m
2,求PA的长.(精确到0.1m)

查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(52):2.8 二次函数的应用(解析版)
题型:解答题
如图,某学校校园内有一块形状为直角梯形的空地ABCD,其中AB∥DC,∠B=90°,AB=100m,BC=80m,CD=40m,现计划在上面建设一个面积为S的矩形综合楼PMBN,其中点P在线段AD上,且PM的长至少为36m.
(1)求边AD的长;
(2)设PA=x(m),求S关于x的函数关系式,并指出自变量x的取值范围;
(3)若S=3300m
2,求PA的长.(精确到0.1m)

查看答案和解析>>
科目:czsx
来源:第23章《二次函数与反比例函数》中考题集(47):23.5 二次函数的应用(解析版)
题型:解答题
如图,某学校校园内有一块形状为直角梯形的空地ABCD,其中AB∥DC,∠B=90°,AB=100m,BC=80m,CD=40m,现计划在上面建设一个面积为S的矩形综合楼PMBN,其中点P在线段AD上,且PM的长至少为36m.
(1)求边AD的长;
(2)设PA=x(m),求S关于x的函数关系式,并指出自变量x的取值范围;
(3)若S=3300m
2,求PA的长.(精确到0.1m)
查看答案和解析>>
科目:czsx
来源:第6章《二次函数》中考题集(51):6.4 二次函数的应用(解析版)
题型:解答题
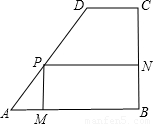
如图,某学校校园内有一块形状为直角梯形的空地ABCD,其中AB∥DC,∠B=90°,AB=100m,BC=80m,CD=40m,现计划在上面建设一个面积为S的矩形综合楼PMBN,其中点P在线段AD上,且PM的长至少为36m.
(1)求边AD的长;
(2)设PA=x(m),求S关于x的函数关系式,并指出自变量x的取值范围;
(3)若S=3300m
2,求PA的长.(精确到0.1m)

查看答案和解析>>
科目:czsx
来源:第27章《二次函数》中考题集(50):27.3 实践与探索(解析版)
题型:解答题
如图,某学校校园内有一块形状为直角梯形的空地ABCD,其中AB∥DC,∠B=90°,AB=100m,BC=80m,CD=40m,现计划在上面建设一个面积为S的矩形综合楼PMBN,其中点P在线段AD上,且PM的长至少为36m.
(1)求边AD的长;
(2)设PA=x(m),求S关于x的函数关系式,并指出自变量x的取值范围;
(3)若S=3300m
2,求PA的长.(精确到0.1m)

查看答案和解析>>
科目:czsx
来源:2005年广东省广州市中考数学试卷(解析版)
题型:解答题
(2005•广州)如图,某学校校园内有一块形状为直角梯形的空地ABCD,其中AB∥DC,∠B=90°,AB=100m,BC=80m,CD=40m,现计划在上面建设一个面积为S的矩形综合楼PMBN,其中点P在线段AD上,且PM的长至少为36m.
(1)求边AD的长;
(2)设PA=x(m),求S关于x的函数关系式,并指出自变量x的取值范围;
(3)若S=3300m
2,求PA的长.(精确到0.1m)

查看答案和解析>>
科目:czsx
来源:第26章《二次函数》中考题集(48):26.3 实际问题与二次函数(解析版)
题型:解答题
如图,某学校校园内有一块形状为直角梯形的空地ABCD,其中AB∥DC,∠B=90°,AB=100m,BC=80m,CD=40m,现计划在上面建设一个面积为S的矩形综合楼PMBN,其中点P在线段AD上,且PM的长至少为36m.
(1)求边AD的长;
(2)设PA=x(m),求S关于x的函数关系式,并指出自变量x的取值范围;
(3)若S=3300m
2,求PA的长.(精确到0.1m)

查看答案和解析>>

 如图,校园要建苗圃,其形状如直角梯形,有两边借用夹角为135°的两面墙,另外两边是总长为30m的铁栅栏.
如图,校园要建苗圃,其形状如直角梯形,有两边借用夹角为135°的两面墙,另外两边是总长为30m的铁栅栏. 如图,校园要建苗圃,其形状如直角梯形,有两边借用夹角为135°的两面墙,另外两边是总长为30m的铁栅栏.
如图,校园要建苗圃,其形状如直角梯形,有两边借用夹角为135°的两面墙,另外两边是总长为30m的铁栅栏.







 某小区要建一个花圃,花圃形状是由一个直角三角形和一个半圆形构成.具体的边长如图所示,其中直角三角形斜边AC为5米,直角边AB为b米,直角边BC为2a米.
某小区要建一个花圃,花圃形状是由一个直角三角形和一个半圆形构成.具体的边长如图所示,其中直角三角形斜边AC为5米,直角边AB为b米,直角边BC为2a米. BC=80m,CD=40m,现计划在上面建设一个面积为S的矩形综合楼PMBN,其中点P在线段AD上,且PM的长至少为36m.
BC=80m,CD=40m,现计划在上面建设一个面积为S的矩形综合楼PMBN,其中点P在线段AD上,且PM的长至少为36m.






