精英家教网 >
试题搜索列表 >\在三角形ACB中,∠ACB=90度,CD垂直AB于D(1)求证:∠ACD=∠B
\在三角形ACB中,∠ACB=90度,CD垂直AB于D(1)求证:∠ACD=∠B答案解析
科目:czsx
来源:
题型:
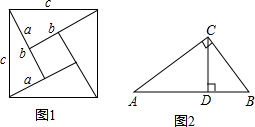
我们发现,用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题,这种方法称为等面积法,这是一种重要的数学方法.请你用等面积法来探究下列两个问题:
(1)如图1是著名的赵爽弦图,由四个全等的直角三角形拼成,请你用它来验证勾股定理;
(2)如图2,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC=4,BC=3,求CD的长度.
查看答案和解析>>
科目:czsx
来源:
题型:
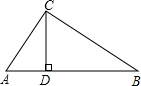
如图,直角三角形ACB中,∠ACB=90°,CD是AB边上的高.若AC=6cm,BC=8cm,那么CD=
cm.
查看答案和解析>>
科目:czsx
来源:
题型:
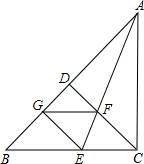
如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠BAC的平分线AE交CD于F,EG⊥AB于G.
(1)求证:△AEG≌△AEC;
(2)△CEF是否为等腰三角形,请证明你的结论;
(3)四边形GECF是否为菱形,请证明你的结论.
查看答案和解析>>
科目:czsx
来源:
题型:
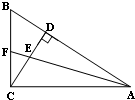
19、如图,已知△ABC中,∠ACB=90°,CD是AB边上的高,AF是∠BAC的平分线且与CD交于点E.
求证:△CEF是等腰三角形.
查看答案和解析>>
科目:czsx
来源:
题型:
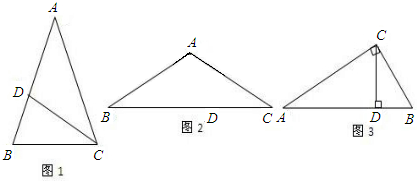
黄金分割比是生活中比较多见的一种长度比值,它能给人许多美感和科学性,我们初中阶段学过的许多几何图形也有着类似的边长比例关系.例如我们熟悉的顶角是36°的等腰三角形,其底与腰之比就为黄金分割比
,底角平分线与腰的交点为黄金分割点.
(1)如图1,在△ABC中,∠A=36°,AB=AC,∠ACB的角平分线CD交腰AB于点D,请你证明点D是腰AB的黄金分割点;
(2)如图2,在△ABC中,AB=AC,若
=,则请你求出∠A的度数;
(3)如图3,如果在Rt△ABC中,∠ACB=90°,CD为AB上的高,∠A、∠B、∠ACB的对边分别为a,b,c.若点D是AB的黄金分割点,那么该直角三角形的三边a,b,c之间是什么数量关系?并证明你的结论.
查看答案和解析>>
科目:czsx
来源:
题型:
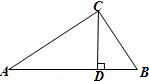
11、如图,在△ABC中,∠ACB=90°,CD是AB边上的高线,图中相似三角形共有( )
查看答案和解析>>
科目:czsx
来源:
题型:
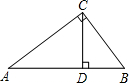
如图,直角三角形ABC中,∠ACB=90°,CD是AB边上的高,且AB=5,AC=4,BC=3,则CD=
.
查看答案和解析>>
科目:czsx
来源:
题型:
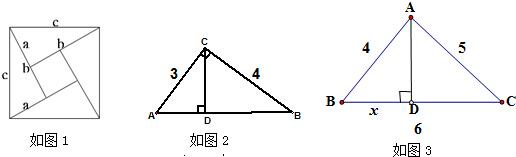
如图1是著名的赵爽弦图,由四个全等的直角三角形拼成,用它可以证明勾股定理,思路是:大正方形的面积有两种求法,一种是等于c
2,另一种是等于四个直角三角形与一个小正方形的面积之和,即
ab×4+(b-a)2,从而得到等式c
2=
ab×4+(b-a)2,化简便得结论a
2+b
2=c
2.这里用两种求法来表示同一个量从而得到等式或方程的方法,我们称之为“双求法”.现在,请你用“双求法”解决下面两个问题
(1)如图2,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC=3,BC=4,求CD的长度.
(2)如图3,在△ABC中,AD是BC边上的高,AB=4,AC=5,BC=6,设BD=x,求x的值.
查看答案和解析>>
科目:czsx
来源:
题型:
在直角三角形ABC中,∠ACB=90°,CD是AB边上的高,AB=10cm,BC=8cm,AC=6cm
(1)求△ABC的面积;
(2)求CD的长;
(3)若△ABC的边AC上的中线是BE,求出△ABE的面积.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在直角三角形ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm,求:
(1)CD的长;
(2)作出△ABC的边AC上的中线BE,并求出△ABE的面积.
查看答案和解析>>
科目:czsx
来源:
题型:
附加题:
(1)若一个角的补角是这个角的余角的3倍,则这个角是
度.
(2)在Rt△ABC中,∠ACB=90°,CD是AB边上的高,若AB=13,BC=12,AC=5,则CD=
.
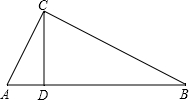
查看答案和解析>>
科目:czsx
来源:
题型:
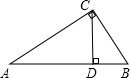
如图,直角三角形ABC中,∠ACB=90°,CD是AB边上的高,且AB=5,AC=4,BC=3,则CD=( )
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在直角三角形ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm.求:
(1)△ABC的面积;
(2)CD的长;
(3)作出△ABC的边AC上的中线BE,并求出△ABE的面积;
(4)作出△BCD的边BC边上的高DF,当BD=11cm时,试求出DF的长.
查看答案和解析>>
科目:czsx
来源:
题型:
在直角三角形中,∠ACB=90°,CD是AB边上的高,AB=10cm,BC=8cm,AC=6cm.
(1)△ABC的面积;
(2)求CD的长?
(3)若△ABC的边AC上的中线是BE,求△ABE的面积.
查看答案和解析>>
科目:czsx
来源:2012-2013学年广东佛山南海盐步中学初二上周质量数学试卷(带解析)
题型:解答题
我们发现,用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题这种方法称为等面积法,这是一种重要的数学方法.请你用等面积法来探究下列两个问题:
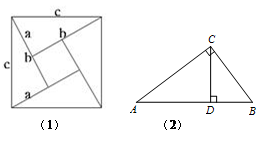
(1)如图1是著名的赵爽弦图,由四个全等的直角三角形拼成,请你用它来验证勾股定理;
(2)如图2,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC= 4,BC=3,求CD的长度.
查看答案和解析>>
科目:czsx
来源:
题型:
在直角三角形中,∠ACB=90°,CD是AB边上的高,AB=10cm,BC=8cm,AC=6cm.
(1)△ABC的面积;
(2)求CD的长?
(3)若△ABC的边AC上的中线是BE,求△ABE的面积.
查看答案和解析>>
科目:czsx
来源:2011年初中毕业升学考试(江苏南京卷)数学解析版
题型:解答题
在直角三角形中,∠ACB=90°,CD是AB边上的高,AB=10cm,BC=8cm,AC=6cm.
(1)△ABC的面积;
(2)求CD的长?
(3)若△ABC的边AC上的中线是BE,求△ABE的面积.
查看答案和解析>>
科目:czsx
来源:2011届河北省廊坊市安次区初三第一次模拟考试数学试题
题型:解答题
在直角三角形中,∠ACB=90°,CD是AB边上的高,AB=10cm,BC=8cm,AC=6cm.
(1)△ABC的面积;
(2)求CD的长?
(3)若△ABC的边AC上的中线是BE,求△ABE的面积.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,在直角三角形ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm,

求:(1)△ABC的面积;
(2)CD的长;
(3)作出△ABC的边AC上的中线BE,并求出△ABE的面积;
(4)作出△BCD的边BC边上的高DF,当BD="11cm" 时,试求出DF的长。
查看答案和解析>>
科目:czsx
来源:2012-2013学年广东佛山南海盐步中学初二上周质量数学试卷(解析版)
题型:解答题
我们发现,用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题这种方法称为等面积法,这是一种重要的数学方法.请你用等面积法来探究下列两个问题:
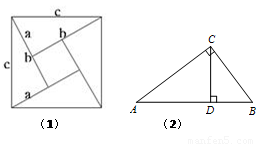
(1)如图1是著名的赵爽弦图,由四个全等的直角三角形拼成,请你用它来验证勾股定理;
(2)如图2,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AC= 4,BC=3,求CD的长度.
查看答案和解析>>

 我们发现,用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题,这种方法称为等面积法,这是一种重要的数学方法.请你用等面积法来探究下列两个问题:
我们发现,用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题,这种方法称为等面积法,这是一种重要的数学方法.请你用等面积法来探究下列两个问题: 如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠BAC的平分线AE交CD于F,EG⊥AB于G.
如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠BAC的平分线AE交CD于F,EG⊥AB于G.

 如图,在直角三角形ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm,求:
如图,在直角三角形ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm,求:
 如图,在直角三角形ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm.求:
如图,在直角三角形ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm.求:

