精英家教网 >
试题搜索列表 >如图,直线ab,cd,ef相交于点o,且ab⊥cd,若∠1=∠3.∠1+∠2=
如图,直线ab,cd,ef相交于点o,且ab⊥cd,若∠1=∠3.∠1+∠2=答案解析
科目:czsx
来源:2016届辽宁抚顺中考模拟试卷(六)数学试卷(解析版)
题型:解答题
菱形ABCD中,两条对角线AC、BD相交于点O,点E和点F分别是BC和CD上一动点,且∠EOF+∠BCD=180°,连接EF.

(1)如图2,当∠ABC=60°时,猜想三条线段CE、CF、AB之间的数量关系 ;
(2)如图1,当∠ABC=90°时,若AC=4 ,BE=
,BE=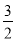 ,求线段EF的长;
,求线段EF的长;
(3)如图3,当∠ABC=90°,将∠EOF的顶点移到AO上任意一点O′处,∠EO′F绕点O′旋转,仍满足∠EO′F+∠BCD=180°,O′E交BC的延长线一点E,射线O′F交CD的延长线上一点F,连接EF探究在整个运动变化过程中,线段CE、CF,O′C之间满足的数量关系,请直接写出你的结论.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
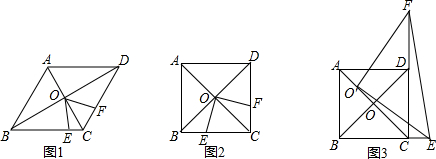
7.菱形ABCD中,两条对角线AC、BD相交于点O,点E和点F分别是BC和CD上一动点,且∠EOF+∠BCD=180°,连接EF.
(1)如图2,当∠ABC=60°时,猜想三条线段CE、CF、AB之间的数量关系CE+CF=$\frac{1}{2}$AB.;
(2)如图1,当∠ABC=90°时,若AC=4$\sqrt{2}$,BE=$\frac{3}{2}$,求线段EF的长;
(3)如图3,当∠ABC=90°,将∠EOF的顶点移到AO上任意一点O′处,∠EO′F绕点O′旋转,仍满足∠EO′F+∠BCD=180°,O′E交BC的延长线一点E,射线O′F交CD的延长线上一点F,连接EF探究在整个运动变化过程中,线段CE、CF,O′C之间满足的数量关系,请直接写出你的结论.
查看答案和解析>>
科目:czsx
来源:2011年黑龙江省哈尔滨市南岗区中考数学一模试卷(解析版)
题型:解答题
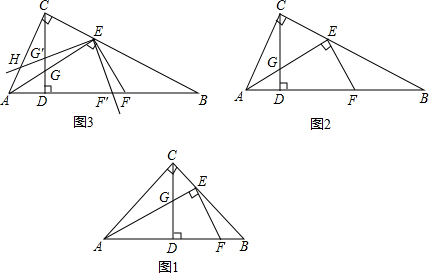
Rt△ABC中,∠ACB=90°,CD为高线,点E在边BC上,且BE=2EC,连接AE,EF⊥AE,与边AB相交于点F.
(1)如图1,当tan∠BAC=1时,求证:EF=2EG
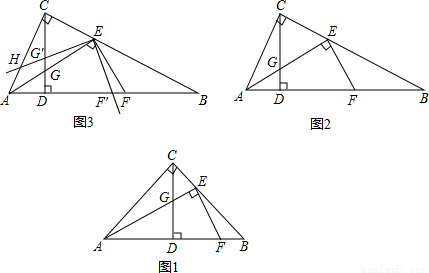
(2)如图2,当tan∠BAC=2时,则线段EF、EG的数量关系为______;
(3)如图3,在(2)的条件下,将∠FEG绕点E顺时针旋转α,旋转后EF边所在的直线与边AB相交于点F′,EG边所在的直线与边AC相交于点H,与高线CD相交于点G′,若AH=3
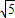
,且
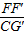
=

,求线段G′H的长.
查看答案和解析>>
科目:czsx
来源:
题型:
(2011•南岗区一模)Rt△ABC中,∠ACB=90°,CD为高线,点E在边BC上,且BE=2EC,连接AE,EF⊥AE,与边AB相交于点F.
(1)如图1,当tan∠BAC=1时,求证:EF=2EG
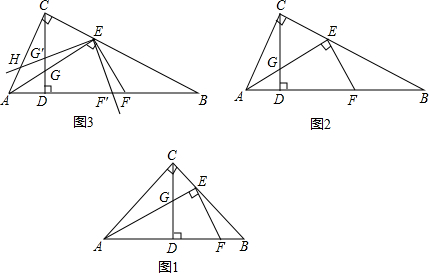
(2)如图2,当tan∠BAC=2时,则线段EF、EG的数量关系为
EF=EG
EF=EG
;
(3)如图3,在(2)的条件下,将∠FEG绕点E顺时针旋转α,旋转后EF边所在的直线与边AB相交于点F′,EG边所在的直线与边AC相交于点H,与高线CD相交于点G′,若AH=3
,且
=
,求线段G′H的长.
查看答案和解析>>
科目:czsx
来源:
题型:
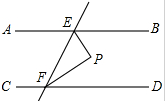
如图所示,若AB∥CD,直线EF与AB、CD分别相交于点E,F,∠FEB与∠EFD的平分线相交于点P,且∠EFD=60°,求∠BEP的度数.
查看答案和解析>>
科目:czsx
来源:2017届福建省九年级上学期第二次阶段性测试数学试卷(解析版)
题型:解答题
如图直角坐标系中,矩形ABCD的边BC在x轴上,点B、D的坐标分别为B(1,0),D(3,3).

(1)点C的坐标 ;
(2)若反比例函数 的图象经过直线AC上的点E,且点E的坐标为(2,m),求m的值及反比例函数的解析式;
的图象经过直线AC上的点E,且点E的坐标为(2,m),求m的值及反比例函数的解析式;
(3)若(2)中的反比例函数的图象与CD相交于点F,连接EF,在直线AB上找一点P,使得 ,求点P的坐标.
,求点P的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
19.如图1,正方形ABCD中,点E、F分别为边AD、CD上的点,且DE=CF,AF、BE相交于点G.

(1)问:线段AF和BE有怎样的位置关系和数量关系?(直接写出结论,不必证明)
答:线段AF和BE的位置关系是互相垂直,数量关系是相等.
(2)若点E、F分别运动到边AD的延长线和边DC的延长线上,其他条件均保持不变(如图2),此时连接BF和EF,M、N、P、Q分别为AE、EF、BF、AB的中点,请判断四边形MNPQ是“矩形、菱形、正方形”中的哪一种?并写出证明过程.
查看答案和解析>>
科目:czsx
来源:
题型:
已知:如图,直线EF分别交AB,CD于点E,F,且∠AEF=66°,∠BEF的平分线与∠DFE的平分线相交于点P.

(1)求∠PEF的度数;
(2)若已知直线AB∥CD,求∠P的度数.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
已知:如图,直线EF分别交AB,CD于点E,F,且∠AEF=66°,∠BEF的平分线与∠DFE的平分线相交于点P.
(1)求∠PEF的度数;
(2)若已知直线AB∥CD,求∠P的度数.
查看答案和解析>>
科目:czsx
来源:河南省期中题
题型:解答题
已知:如图,直线EF分别交AB,CD于点E,F,且∠AEF=66°,∠BEF的平分线与∠DFE的平分线相交于点P.
(1)求∠PEF的度数;
(2)若已知直线AB∥CD,求∠P的度数.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,在Rt△ABC中,∠C=90°,AB=50,AC=30,D,E,F分别是AC,AB,BC的中点.点P从点D出发沿折线DE-EF-FC-CD以每秒7个单位长的速度匀速运动;点Q从点B出发沿BA方向以每秒4个单位长的速度匀速运动,过点Q作射线QK⊥AB,交折线BC-CA于点G.点P,Q同时出发
,当点P绕行一周回到点D时停止运动,点Q也随之停止.设点P,Q运动的时间是t秒(t>0).
(1)D,F两点间的距离是
;
(2)射线QK能否把四边形CDEF分成面积相等的两部分?若能,求出t的值;若不能,说明理由;
(3)当点P运动到折线EF-FC上,且点P又恰好落在射线QK上时,求t的值;
(4)连接PG,当PG∥AB时,请直接写出t的值.
查看答案和解析>>
科目:czsx
来源:
题型:
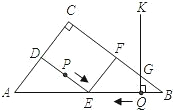
如图1,在直角梯形ABCD中,AD∥BC,∠D=90°,AD=9cm,CD=12cm,BC=15cm.点P由点C出发沿CA方向匀速运动,速度为1cm/s;同时,线段EF由AB出发沿AD方向匀速运动,速度为1cm/s,且与AC交于Q点,连接PE,PF.当点P与点Q相遇时,所有运动停止.若设运动时间为t(s).
(1)求AB的长度;
(2)当PE∥CD时,求出t的值;
(3)①设△PEF的面积为S,求S关于t的函数关系式;
②如图2,当△PEF的外接圆圆心O恰在EF的中点时,则t的值为
.(直接写出答案)

查看答案和解析>>
科目:czsx
来源:
题型:
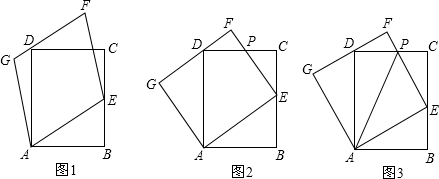
如图1、图2、图3,在矩形ABCD中,E是BC边上的一点,以AE为边作平行四边形AEFG,使点D在AE的对边FG上,
(1)如图1,试说明:平行四边形AEFG的面积与矩形ABCD的面积相等;
(2)如图2,若平行四边形AEFG是矩形,EF与CD交于点P,试说明:A、E、P、D四点在同一个圆上;
(3)如图3,若AB<BC,平行四边形AEFG是正方形,且D是FG的中点,EF交CD于点P,连接PA,判断以FG为直径的圆与直线PA的位置关系,并说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
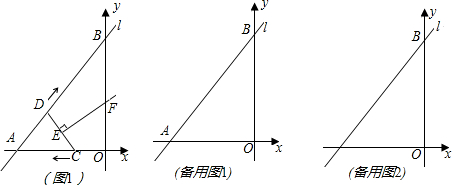
如图1,已知直线l的解析式为
y=x+4,它与x轴、y轴分别相交于A、B两点.点C从点O出发沿OA以每秒1个单位的速度向点A匀速运动;点D从点A出发沿AB以每秒1个单位长的速度向点B匀速运动,点C、D同时出发,当点C到达点A时同时停止运动.伴随着C、D的运动,EF始终保持垂直平分CD,垂足为E,且EF交折线AB-BO-AO于点F.
(1)直接写出A、B两点的坐标;
(2)设点C、D的运动时间是t秒(t>0).
①用含t的代数式分别表示线段AD和AC的长度;
②在点F运动的过程中,四边形BDEF能否成为直角梯形?若能,求t的值;若不能,请说明理由.(可利用备用图解题)
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在直角坐标系中,矩形ABCD的边BC在x轴上,点B、D的坐标分别为B(1,0),D(3,3).
(1)直接写出点C的坐标;
(2)若反比例函数
y=的图象经过直线AC上的点E,且点E的坐标为(2,m),求m的值及反比例函数的解析式;
(3)若(2)中的反比例函数的图象与CD相交于点F,连接EF,在线段AB上(端点除外)找一点P,使得S
△PEF=S
△CEF,并求出点P的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
如图:平面直角坐标系中,△ABC的三个顶点的坐标为A(a,0),B(b,0),C(0,c),且a,b,c满足
+|b-2|+(c-b)2=0.点D为线段OA上一动点,连接CD.
(1)判断△ABC的形状并说明理由;
(2)如图,过点D作CD的垂线,过点B作BC的垂线,两垂线交于点G,作GH⊥AB于H,求证:
=;
(3)如图,若点D到CA、CO的距离相等,E为AO的中点,且EF∥CD交y轴于点F,交CA于M.求
的值.

查看答案和解析>>
科目:czsx
来源:
题型:

如图,直线AB、CD、EF相交于点O,且AB⊥CD,若∠BOE=70°,则∠DOF的度数为
20°
20°
.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,已知直线AB∥CD∥EF,∠POQ=90°,它的顶点O在CD上,两边分别与AB、EF相交于点P,点Q,射线OC
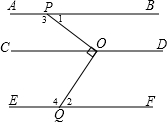
始终在∠POQ的内部.
(1)求∠1+∠2的度数;
(2)直接写出∠3与∠4的数量关系:
270°
270°
.
(3)若∠POQ的度数为α,且0°<α<180°,其余条件不变,则∠3与∠4的数量关系为
∠3+∠4=360°-α
∠3+∠4=360°-α
.(用含α的式子表示)
查看答案和解析>>
科目:czsx
来源:
题型:
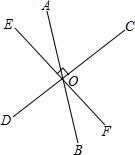
如图所示,直线AB、CD、EF相交于点O,且EF⊥CD,若∠AOE=30°,则∠AOC=
60
60
°,∠AOF=
150
150
°,∠BOC=
120
120
°.
查看答案和解析>>


 ,BE=
,BE=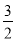 ,求线段EF的长;
,求线段EF的长;
 ,且
,且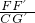 =
=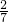 ,求线段G′H的长.
,求线段G′H的长.
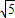 ,且
,且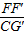 =
= ,求线段G′H的长.
,求线段G′H的长.

 的图象经过直线AC上的点E,且点E的坐标为(2,m),求m的值及反比例函数的解析式;
的图象经过直线AC上的点E,且点E的坐标为(2,m),求m的值及反比例函数的解析式; ,求点P的坐标.
,求点P的坐标.



 ,当点P绕行一周回到点D时停止运动,点Q也随之停止.设点P,Q运动的时间是t秒(t>0).
,当点P绕行一周回到点D时停止运动,点Q也随之停止.设点P,Q运动的时间是t秒(t>0).


 如图,在直角坐标系中,矩形ABCD的边BC在x轴上,点B、D的坐标分别为B(1,0),D(3,3).
如图,在直角坐标系中,矩形ABCD的边BC在x轴上,点B、D的坐标分别为B(1,0),D(3,3).
 始终在∠POQ的内部.
始终在∠POQ的内部. 如图所示,直线AB、CD、EF相交于点O,且EF⊥CD,若∠AOE=30°,则∠AOC=
如图所示,直线AB、CD、EF相交于点O,且EF⊥CD,若∠AOE=30°,则∠AOC=