练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >请你将﹣4.﹣3.﹣2.﹣1,0,1,2,3,4这9个数

    请你将﹣4.﹣3.﹣2.﹣1,0,1,2,3,4这9个数答案解析

    科目：czdl 来源：2016年初中毕业升学考试（山东泰安卷）地理（解析版） 题型：综合题

    生活实验室 如果你是一名娱乐设施公司的土地资源策划者，公司正在考虑购买同纬度的几个城市中的土地．经过筛选确定了美国北纬39度上的两个备选城市．你的工作是决定哪个城市最适合建适水上公园，哪个城市最适合建造滑雪游览中心．

    问题：根据气候资料，你怎样确定建造地点．

    技能：绘制图表，分析数据，得出结论．

    气候资料

    A华盛顿

    1月

    2月

    3月

    4月

    5月

    6月

    7月

    8月

    9月

    10月

    11月

    12月

    平均最高气温℃

    6

    8

    14

    19

    24

    29

    32

    31

    27

    21

    14

    8

    平均最低气温℃

    ﹣3

    ﹣2

    3

    8

    14

    19

    22

    21

    17

    10

    5

    0

    平均降水量mm

    69

    69

    81

    69

    94

    86

    97

    99

    84

    76

    79

    79

    有雪的月份

    ★

    ★

    ★

    轻微

    ﹣

    ﹣

    ﹣

    ﹣

    ﹣

    轻微

    ★

    ★

    B科罗拉多某市

    1月

    2月

    3月

    4月

    5月

    6月

    7月

    8月

    9月

    10月

    11月

    12月

    平均最高气温℃

    5

    7

    10

    16

    21

    26

    29

    27

    23

    18

    11

    6

    平均最低气温℃

    ﹣9

    ﹣7

    ﹣4

    1

    6

    11

    14

    13

    8

    2

    ﹣4

    ﹣8

    平均降水量mm

    8

    10

    23

    30

    56

    58

    74

    76

    33

    20

    13

    13

    有雪的月份

    ★

    ★

    ★

    ★

    ★

    ﹣

    ﹣

    ﹣

    轻微

    ★

    ★

    ★

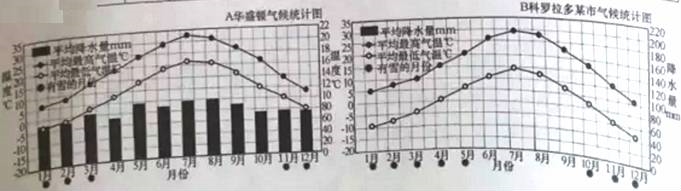
    材料：（略）

    步骤：分小组工作，每人将两个城市的资料绘制成图（见上图）．请你把“B科罗拉多气候统计图”上“各月平均降水量”绘制出来．

    分析和结论：比较你绘制的气候统计图与观察结果，回答下列问题．

    ①这两个城市中，哪个城市各月的气温变化幅度较大．

    ②这两个城市中，哪个城市的年降水量较大．且各月降水量比较均匀．

    ③这两个城市处在同一纬度上，为什么它们的气候统计资料差距这么人大？

    应用：哪个城市适合建造水公园？ 哪个城市适合建造滑雪游览中心？ 在建造这些娱乐场所时，还应考虑哪些其它因素？ ．

    查看答案和解析>>

    科目：czsx 来源：2016届福建泉州晋江市中考二模数学试卷（解析版） 题型：解答题

    将三张质地相同并分别标有数字1、2、3的卡片，背面朝上放在桌面上，洗匀后，甲同学从中随机抽取一张卡片．

    （1）甲同学抽到卡片上的数恰好是方程x2﹣4x+3=0的根的概率为 ；

    （2）甲乙两人约定：甲先随机抽取一张卡片后，背面朝上放回桌面洗匀，然后乙再随机抽取一张卡片，若两人所抽取卡片上的数字恰好是方程x2﹣4x+3=0的两个根，则甲获胜；否则乙获胜．请你通过列表或画树状图的方法，说明这个游戏是否公平？

    查看答案和解析>>

    科目：czsx 来源：同步题 题型：解答题

    现有四个有理数3，4，﹣6，10，将这四个数（每个数用且只能用一次）进行加减乘除四则运算，使其运算的结果是24，请你写出一个符合条件的算式

    查看答案和解析>>

    科目：czsx 来源：湖北省期中题 题型：填空题

    现有四个有理数3，4，﹣6，10，将这四个数（每个数用且只能用一次）进行加减乘除四则运算，使其运算的结果是24，请你写出一个符合条件的算式（    ）．

    查看答案和解析>>

    科目：czsx 来源：同步题 题型：填空题

    现有四个有理数3，4，﹣6，10，将这四个数（每个数用且只能用一次）进行加减乘除四则运算，使其运算的结果是24，请你写出一个符合条件的算式（    ）．

    查看答案和解析>>

    科目：czsx 来源：湖北省期末题 题型：填空题

    现有四个有理数3，4，﹣6，10，将这四个数（每个数用且只能用一次）进行加减乘除四则运算，使其运算的结果是24，请你写出一个符合条件的算式（    ）．

    查看答案和解析>>

    科目：czsx 来源：期中题 题型：填空题

    现有四个有理数3，4，﹣6，10，将这四个数（每个数用且只能用一次）进行加减乘除四则运算，使其运算的结果是24，请你写出一个符合条件的算式（    ）．

    查看答案和解析>>

    科目：czsx 来源：2015-2016学年安徽省阜阳市太和县七年级上学期第一次月考数学试卷（解析版） 题型：填空题

    （2005•山西）现有四个有理数3，4，﹣6，10，将这四个数（每个数用且只能用一次）进行加减乘除四则运算，使其运算的结果是24，请你写出一个符合条件的算式 ．

    查看答案和解析>>

    科目：czsx 来源： 题型：


    小明做作业时，不小心将方程中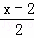﹣1=+●的一个常数污染了看不清楚，怎么办呢？

    （1）小红告诉他该方程的解是x=3，那么这个常数应是多少呢？

    （2）小芳告诉他该方程的解是负数，并且这个常数是负整数，请你试求该方程的解．

    （友情提醒：设这个常数为m．）

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

    已知：关于x的一元二次方程mx2﹣（4m+1）x+3m+3="0" （m＞1）．
    （1）求证：方程有两个不相等的实数根；
    （2）设方程的两个实数根分别为x1，x2（其中x1＞x2），若y是关于m的函数，且y=x1﹣3x2，求这个函数的解析式；
    （3）将（2）中所得的函数的图象在直线m=2的左侧部分沿直线m=2翻折，图象的其余部分保持不变，得到一个新的图象．请你结合这个新的图象回答：当关于m的函数y=2m+b的图象与此图象有两个公共点时，b的取值范围．

    查看答案和解析>>

    科目：czsx 来源：不详 题型：解答题

    已知：关于x的一元二次方程mx2﹣（4m+1）x+3m+3="0" （m＞1）．
    （1）求证：方程有两个不相等的实数根；
    （2）设方程的两个实数根分别为x1，x2（其中x1＞x2），若y是关于m的函数，且y=x1﹣3x2，求这个函数的解析式；
    （3）将（2）中所得的函数的图象在直线m=2的左侧部分沿直线m=2翻折，图象的其余部分保持不变，得到一个新的图象．请你结合这个新的图象回答：当关于m的函数y=2m+b的图象与此图象有两个公共点时，b的取值范围．

    查看答案和解析>>

    科目：czsx 来源：2014年北京市东城区中考一模数学试卷（解析版） 题型：解答题

    已知：关于x的一元二次方程mx2﹣（4m+1）x+3m+3=0 （m＞1）．

    （1）求证：方程有两个不相等的实数根；

    （2）设方程的两个实数根分别为x1，x2（其中x1＞x2），若y是关于m的函数，且y=x1﹣3x2，求这个函数的解析式；

    （3）将（2）中所得的函数的图象在直线m=2的左侧部分沿直线m=2翻折，图象的其余部分保持不变，得到一个新的图象．请你结合这个新的图象回答：当关于m的函数y=2m+b的图象与此图象有两个公共点时，b的取值范围．

     

     

    查看答案和解析>>

    科目：czsx 来源：2014-2015学年河南省九年级下学期综合练习一考试数学试卷（解析版） 题型：解答题

    已知：关于x的一元二次方程mx2﹣（4m+1）x+3m+3=0 （m＞1）．

    （1）求证：方程有两个不相等的实数根；

    （2）设方程的两个实数根分别为x1，x2（其中x1＞x2），若y是关于m的函数，且y=x1﹣3x2，求这个函数的解析式；

    （3）将（2）中所得的函数的图象在直线m=2的左侧部分沿直线m=2翻折，图象的其余部分保持不变，得到一个新的图象．请你结合这个新的图象回答：当关于m的函数y=2m+b的图象与此图象有两个公共点时，b的取值范围．

    查看答案和解析>>

    科目：czsx 来源：2013年初中数学单元提优测试卷-公式法（带解析） 题型：解答题

    请看下面的问题：把x4+4分解因式
    分析：这个二项式既无公因式可提，也不能直接利用公式，怎么办呢
    19世纪的法国数学家苏菲•热门抓住了该式只有两项，而且属于平方和（x2）2+（22）2的形式，要使用公式就必须添一项4x2，随即将此项4x2减去，即可得x4+4=x4+4x2+4﹣4x2=（x2+2）2﹣4x2=（x2+2）2﹣（2x）2=（x2+2x+2）（x2﹣2x+2）
    人们为了纪念苏菲•热门给出这一解法，就把它叫做“热门定理”，请你依照苏菲•热门的做法，将下列各式因式分解．
    （1）x4+4y4；（2）x2﹣2ax﹣b2﹣2ab．

    查看答案和解析>>

    科目：czsx 来源：2013年初中数学单元提优测试卷-公式法（解析版） 题型：解答题

    请看下面的问题：把x4+4分解因式

    分析：这个二项式既无公因式可提，也不能直接利用公式，怎么办呢

    19世纪的法国数学家苏菲?热门抓住了该式只有两项，而且属于平方和（x2）2+（22）2的形式，要使用公式就必须添一项4x2，随即将此项4x2减去，即可得x4+4=x4+4x2+4﹣4x2=（x2+2）2﹣4x2=（x2+2）2﹣（2x）2=（x2+2x+2）（x2﹣2x+2）

    人们为了纪念苏菲?热门给出这一解法，就把它叫做“热门定理”，请你依照苏菲?热门的做法，将下列各式因式分解．

    （1）x4+4y4；（2）x2﹣2ax﹣b2﹣2ab．

     

    查看答案和解析>>

    科目：czsx 来源：浙江省期中题 题型：解答题

    这是一个很著名的故事：阿基米德与国王下棋，国王输了，国王问阿基米德要什么奖赏？阿基米德对国王说：“我只要在棋盘上第一格放一粒米，第二格放二粒，第三格放四粒，第四格放十六粒…按这个方法放满整个棋盘就行．”国王以为要不了多少粮食，就随口答应了，结果国王输了．
    （1）我们知道，国际象棋共有64个格子，则在第64格中应放多少米？（用幂表示）
    （2）请探究第（1）中的数的末位数字是多少？（简要写出探究过程．）
    （3）你知道国王输给了阿基米德多少粒米吗？为解决这个问题，我们先来看下面的解题过程：用分数表示无限循环小数：．
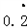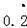    解：设①．等式两边同时乘以10，得10x=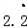②．
    将②﹣①得：9x=2，
    则．
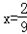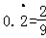    ∴请参照以上解法求出国王输给阿基米德的米粒数（用幂的形式表示）

    查看答案和解析>>

    科目：czsx 来源：广东省期中题 题型：探究题

    数学家高斯在上学时曾经研究过这样一个问题，1+2+3+…+10=？
    经过研究，这个问题的一般性结论是1+2+3+…+n=xn（n+1），其中n为正整数，现在我们来研究一个类似的问题：1×2+2×3+…+n（n+1）=？ 观察下面三个特殊的等式：
    1×2=n（1×2×3﹣0×1×2）
    2×3=x（2×3×4﹣1×2×3）
    3×4=n（3×4×5﹣2×3×4）
    将这三个等式的两边相加，可以得到1×2+2×3+3×4=m×3×4×5=20．读完这段材料，请你计算：
    （1）1×2+2×3+…+100×101=_________；（直接写出结果）
    （2）1×2+2×3+…+n（n+1）；（写出计算过程）
    （3）1×2×3+2×3×4+…+n（n+1）（n+2）=_________．

    查看答案和解析>>

    科目：czsx 来源：不详 题型：解答题

    请看下面的问题：把x4+4分解因式
    分析：这个二项式既无公因式可提，也不能直接利用公式，怎么办呢
    19世纪的法国数学家苏菲•热门抓住了该式只有两项，而且属于平方和（x2）2+（22）2的形式，要使用公式就必须添一项4x2，随即将此项4x2减去，即可得x4+4=x4+4x2+4﹣4x2=（x2+2）2﹣4x2=（x2+2）2﹣（2x）2=（x2+2x+2）（x2﹣2x+2）
    人们为了纪念苏菲•热门给出这一解法，就把它叫做“热门定理”，请你依照苏菲•热门的做法，将下列各式因式分解．
    （1）x4+4y4；（2）x2﹣2ax﹣b2﹣2ab．

    查看答案和解析>>

    科目：czsx 来源：重庆市期末题 题型：探究题

    图1是一个3×3方阵图，每行的三个数、每列的三个数，每斜对角的三个数相加的和均相等．如何把9个连续整数迅速填入一个3×3方阵，使每行、每列、每斜对角的三个数相加的和均相等，是我们祖先早就在研究的问题．古代的“洛书”、汉朝徐岳的“九宫算”就揭示出祖先们得到的神奇填写方法．图1显示出把﹣4，﹣3，﹣2，﹣1，0，1，2，3，4填入一个3×3方阵，使每行、每列、每斜对角的三个数相加的和均相等的一种方法．同学们，你能正确填写吗？马上试一试：
    （1）请观察图1中数字的填写规律，然后将下列各数组中的9个数分别填入图2、图3、图4所示的9个空格中，使得每行的三个数、每列的三个数，每斜对角的三个数相加的和均相等；
    ①6，5，4，3，2，1，0，﹣1，﹣2
    ②9，8，7，6，5，4，3，2，1
    ③﹣8，﹣6，﹣4，﹣2，0，2，4，6，8
    （2）拓展探究：在图5所示 9个空格中，填入5个2和4个﹣2，使得每行、每列、每斜对角的三个数的乘积都是8；
    （3）拓展再探究：将25，24，23，22，21，20，19，18，17，16，15，14，13，12，11，10，9，8，7，6，5，4，3，2，1这25个数分别填入图 6所示25个空格中，使得每行、每列、每斜对角的五个数相加的和均相等．

    查看答案和解析>>

    科目：czsx 来源：2016届北京六十六中九年级上学期期中数学试卷（解析版） 题型：解答题

    已知P（﹣3，m）和 Q（1，m）是抛物线y=x2+bx﹣3上的两点．

    （1）求b的值；

    （2）将抛物线y=x2+bx﹣3的图象向上平移k（是正整数）个单位，使平移后的图象与x轴无交点，求k的最小值；

    （3）将抛物线y=x2+bx﹣3的图象在x轴下方的部分沿x轴翻折，图象的其余部分保持不变，得到一个新的图象，请你结合新图象回答：当直线y=x+n与这个新图象有两个公共点时，求n的取值范围．

    查看答案和解析>>