
科目:czsx 来源: 题型:解答题
科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
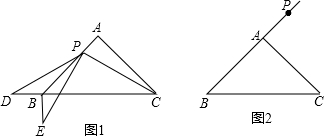
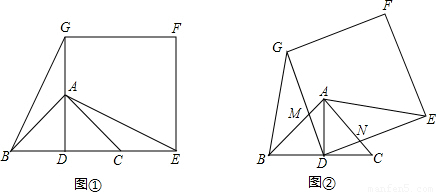
在等腰直角三角形ABC中,∠BAC=90°,AB=AC,直线MN过点A且MN∥BC.以点B为一锐角顶点作Rt△BDE,∠BDE=90°,且点D在直线MN上(不与点A重合).如图1,DE与AC交于点P,易证:BD=DP.(无需写证明过程)
(1)在图2中,DE与CA延长线交于点P,BD=DP是否成立?如果成立,请给予
证明,如果不成立,请说明理由;
(2)在图3中,DE与AC延长线交于点P,BD与DP是否相等?请直接写出你的结论,无需证明.

科目:czsx 来源:2014-2015学年山西省晋中市平遥县九年级下学期4月中考模拟数学试卷(解析版) 题型:解答题
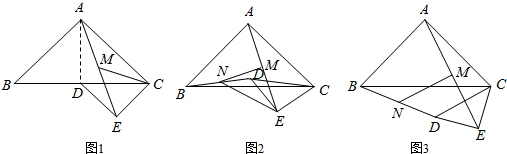
在等腰直角三角形ABC中,∠BAC=90°,AB=AC,直线MN过点A且MN∥BC,过点B为一锐角顶点作Rt△BDE,∠BDE=90°,且点D在直线MN上(不与点A重合),如图1,DE与AC交于点P,易证:BD=DP.(无需写证明过程)

(1)在图2中,DE与CA延长线交于点P,BD=DP是否成立?如果成立,请给予证明;如果不成立,请说明理由;
(2)在图3中,DE与AC延长线交于点P,BD与DP是否相等?请直接写出你的结论,无需证明.
科目:czsx 来源:2013届上海市金山区九年级上学期期末考试数学试卷(带解析) 题型:填空题
已知在等腰直角三角形ABC中,∠BAC=90°,AB=AC=4,将边AB绕着点A旋转至 位置,且
位置,且 与AC边之间的夹角为30°,那么线段
与AC边之间的夹角为30°,那么线段 的长等于_______。
的长等于_______。
科目:czsx 来源:2012-2013学年上海市金山区九年级上学期期末考试数学试卷(解析版) 题型:填空题
已知在等腰直角三角形ABC中,∠BAC=90°,AB=AC=4,将边AB绕着点A旋转至 位置,且
位置,且 与AC边之间的夹角为30°,那么线段
与AC边之间的夹角为30°,那么线段 的长等于_______。
的长等于_______。
科目:czsx 来源:不详 题型:填空题
 位置,且
位置,且 与AC边之间的夹角为30°,那么线段
与AC边之间的夹角为30°,那么线段 的长等于_______。
的长等于_______。科目:gzsx 来源: 题型:
 如图,在等腰直角三角形ABC所在平面内,∠BAC=∠CBD=90°,若
如图,在等腰直角三角形ABC所在平面内,∠BAC=∠CBD=90°,若| AD |
| AB |
| AC |
| A、x+y=1 | ||||
B、x+y=
| ||||
| C、x-y=1 | ||||
D、x-y=
|
科目:czsx 来源:2013-2014学年广东广州协助学校40、铁二、37、八一中学初三上期中数学卷(解析版) 题型:解答题
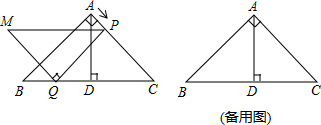
如图1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,D、F分别在AB、AC边上,此时BD=CF,BD⊥CF成立.

(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.

(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G.
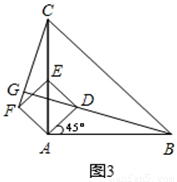
①求证:BD⊥CF;
②当AB=4,AD= 时,求线段FG的长.
时,求线段FG的长.
科目:czsx 来源:不详 题型:解答题



 时,求线段FG的长.
时,求线段FG的长.科目:czsx 来源: 题型:
如图1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,D、F分别在AB、AC边上,此时BD=CF,BD⊥CF成立.
(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G.
①求证:BD⊥CF;
②当AB=4,AD=![]() 时,求线段FG的长.
时,求线段FG的长.
 |
科目:czsx 来源: 题型:填空题
科目:czsx 来源: 题型:解答题
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:解答题

科目:czsx 来源:不详 题型:解答题

科目:czsx 来源:2012年广东省汕头市潮阳区中考数学模拟试卷(二)(解析版) 题型:解答题
科目:czsx 来源: 题型:填空题
 如图,在等腰直角三角形ABC中,∠BAC=90°,P为BC中点,D是BC上的任意一点,DE⊥AC,DF⊥AB,若AE=$\sqrt{2}$,BC=8,则PE=$\sqrt{10}$.
如图,在等腰直角三角形ABC中,∠BAC=90°,P为BC中点,D是BC上的任意一点,DE⊥AC,DF⊥AB,若AE=$\sqrt{2}$,BC=8,则PE=$\sqrt{10}$. 科目:czsx 来源: 题型:解答题
科目:gzsx 来源: 题型:填空题
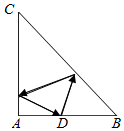 如图,△ABC为等腰直角三角形,∠BAC=90°,AB=2,BD=1,一束光线从点D射入,先后经过斜边BC与直角边AC反射后,恰好从点D射出,则该光线在三角形内部所走的路程是$\sqrt{10}$.
如图,△ABC为等腰直角三角形,∠BAC=90°,AB=2,BD=1,一束光线从点D射入,先后经过斜边BC与直角边AC反射后,恰好从点D射出,则该光线在三角形内部所走的路程是$\sqrt{10}$.