
科目:gzsx 来源: 题型:
|
| x2 |
| 4 |
|
| π |
| 2 |
科目:gzsx 来源:福建 题型:解答题
|
| x2 |
| 4 |
|
| π |
| 2 |
科目:gzsx 来源:2011年福建省高考数学试卷(理科)(解析版) 题型:解答题
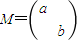 (其中a>0,b>0).
(其中a>0,b>0).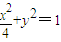 ,求a,b的值.
,求a,b的值.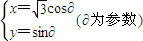 .
. ),判断点P与直线l的位置关系;
),判断点P与直线l的位置关系;科目:czsx 来源: 题型:
| b |
| a |
|
|
| b |
| a |
| 2-3x |
| 2x-1 |
科目:czsx 来源: 题型:阅读理解
 阅读材料,解答问题.
阅读材料,解答问题.科目:czsx 来源: 题型:解答题
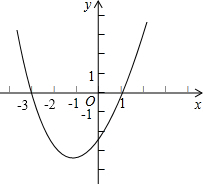 阅读材料,解答问题.
阅读材料,解答问题.科目:czsx 来源:2012年4月份中考数学模拟试卷(十五)(解析版) 题型:解答题
科目:czsx 来源:2012年湖北省黄冈市麻城市中考数学模拟试卷(解析版) 题型:解答题

科目:czsx 来源:不详 题型:解答题
|
|
| 3x-7 |
| 2x-9 |
科目:czsx 来源: 题型:阅读理解
|
|
| 3x-7 |
| 2x-9 |
科目:czsx 来源: 题型:解答题
科目:czsx 来源: 题型:阅读理解
| 5 |
| 3 |
|
|
| 5x-1 |
| 2x-3 |