科目：czsx
来源：
题型：解答题
在一次数学单元检测中，有这样一道题：“若整式（4x2-3ax+x+18）-（3x2+5ax-2x）-（x2+ax-2）的值与字母x无关，求a的值．”小明同学反复思考，总感到无法下手，请你帮小明同学解答此题．
查看答案和解析>>
科目：czsx
来源：
题型：
在一次数学单元检测中，有这样一道题：“若整式（4x2-3ax+x+18）-（3x2+5ax-2x）-（x2+ax-2）的值与字母x无关，求a的值．”小明同学反复思考，总感到无法下手，请你帮小明同学解答此题．
查看答案和解析>>
科目：gzsx
来源：
题型：选择题
16．若关于x的不等式a-ax＞e
x（2x-1）（a＞-1）有且仅有两个整数解，则实数a的取值范围为（ ）
| A． | （-$\frac{3}{4}$，$\frac{5}{3{e}^{2}}$] | | B． | （-1，$\frac{3}{2e}$] | | C． | （-$\frac{3}{2e}$，-$\frac{5}{3{e}^{2}}$] | | D． | （-$\frac{3}{4}$，-$\frac{5}{3{e}^{2}}$） |
查看答案和解析>>
科目：czsx
来源：
题型：
若不等式组
的整数解是关于x的方程2x-4=ax的根，求a的值．
查看答案和解析>>
科目：czsx
来源：
题型：
若不等式组
的整数解是关于x的方程2x-4=ax的解，则a的值为
．
查看答案和解析>>
科目：czsx
来源：
题型：
若不等式组
的整数解是关于x的方程2x-4=ax的解，求a的值．
查看答案和解析>>
科目：czsx
来源：
题型：填空题
若不等式组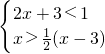
的整数解是关于x的方程2x-4=ax的解，则a的值为________．
查看答案和解析>>
科目：czsx
来源：
题型：解答题
若不等式组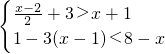
的整数解是关于x的方程2x-4=ax的解，求a的值．
查看答案和解析>>
科目：czsx
来源：
题型：解答题
若不等式组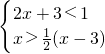整数解是关于x的方程2x-4=ax的根，求a的值．
查看答案和解析>>
科目：czsx
来源：不详
题型：填空题
若不等式组
的整数解是关于x的方程2x-4=ax的解，则a的值为______．
查看答案和解析>>
科目：czsx
来源：乐山
题型：解答题
若不等式组
整数解是关于x的方程2x-4=ax的根，求a的值．
查看答案和解析>>
科目：czsx
来源：河北省模拟题
题型：解答题
若不等式组
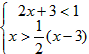
的整数解是关于x的方程2x-4=ax的根，求a的值。
查看答案和解析>>
科目：czsx
来源：2012年湖北省荆州市中考数学模拟试卷（四）（解析版）
题型：解答题
若不等式组
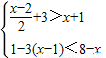
的整数解是关于x的方程2x-4=ax的解，求a的值．
查看答案和解析>>
科目：czsx
来源：2011年浙江省十校联考中考数学模拟试卷（4月份）（解析版）
题型：解答题
若不等式组
整数解是关于x的方程2x-4=ax的根，求a的值．
查看答案和解析>>
科目：czsx
来源：2011年河北省唐山市古冶区中考数学一模试卷（解析版）
题型：解答题
若不等式组
整数解是关于x的方程2x-4=ax的根，求a的值．
查看答案和解析>>
科目：gzsx
来源：
题型：解答题
若函数f（x）满足：在定义域内存在实数x0，使f（x0+k）=f（x0）+f（k）（k为常数），则称“f（x）关于k可线性分解”．
（1）函数f（x）=2x+x2是否关于1可线性分解？请说明理由；
（2）已知函数g（x）=lnx-ax+1（a＞0）关于a可线性分解，求a的范围；
（3）在（2）的条件下，当a取最小整数时；
（i）求g（x）的单调区间；
（ii）证明不等式：（n!）2≤en（n-1）（n∈N*）．
查看答案和解析>>
科目：gzsx
来源：成都模拟
题型：解答题
若函数f（x）满足：在定义域内存在实数x0，使f（x0+k）=f（x0）+f（k）（k为常数），则称“f（x）关于k可线性分解”．
（1）函数f（x）=2x+x2是否关于1可线性分解？请说明理由；
（2）已知函数g（x）=lnx-ax+1（a＞0）关于a可线性分解，求a的范围；
（3）在（2）的条件下，当a取最小整数时；
（i）求g（x）的单调区间；
（ii）证明不等式：（n!）2≤en（n-1）（n∈N*）．
查看答案和解析>>
科目：gzsx
来源：2013年四川省成都市高考数学一诊模拟试卷2（理科）（解析版）
题型：解答题
若函数f（x）满足：在定义域内存在实数x，使f（x+k）=f（x）+f（k）（k为常数），则称“f（x）关于k可线性分解”．
（1）函数f（x）=2x+x2是否关于1可线性分解？请说明理由；
（2）已知函数g（x）=lnx-ax+1（a＞0）关于a可线性分解，求a的范围；
（3）在（2）的条件下，当a取最小整数时；
（i）求g（x）的单调区间；
（ii）证明不等式：（n!）2≤en（n-1）（n∈N*）．
查看答案和解析>>
科目：gzsx
来源：2012年湖北省黄冈市高三3月质量检测数学试卷（理科）（解析版）
题型：解答题
若函数f（x）满足：在定义域内存在实数x，使f（x+k）=f（x）+f（k）（k为常数），则称“f（x）关于k可线性分解”．
（1）函数f（x）=2x+x2是否关于1可线性分解？请说明理由；
（2）已知函数g（x）=lnx-ax+1（a＞0）关于a可线性分解，求a的范围；
（3）在（2）的条件下，当a取最小整数时；
（i）求g（x）的单调区间；
（ii）证明不等式：（n!）2≤en（n-1）（n∈N*）．
查看答案和解析>>
科目：czsx
来源：
题型：
若不等式5(x–2)+8<6(x–1)+7的最小整数解是方程2x－ax=3的解，
则a的值为 ．【原创】
查看答案和解析>>
