科目:czsx 来源: 题型:
 如图:AB是半圆的直径,O是圆心,C、D是半圆上的两点,若AB=4,弦AC=CD=1.
如图:AB是半圆的直径,O是圆心,C、D是半圆上的两点,若AB=4,弦AC=CD=1.科目:czsx 来源: 题型:
 交线段AD的延长线于点F.
交线段AD的延长线于点F. | AD |
科目:czsx 来源: 题型:
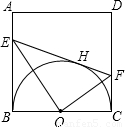
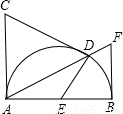
 如图,AB是半圆的直径,AC⊥AB,AC=AB,在半圆上任取一点D,过点D作DE⊥CD,交直径AB于点E,BF⊥AB,交线段AD的延长线于点F,问图中除了AB=AC外,是否还有其他两条线段相等?如果有,指出这两条相等的线段,并给出证明;如果没有,也要说明理由.
如图,AB是半圆的直径,AC⊥AB,AC=AB,在半圆上任取一点D,过点D作DE⊥CD,交直径AB于点E,BF⊥AB,交线段AD的延长线于点F,问图中除了AB=AC外,是否还有其他两条线段相等?如果有,指出这两条相等的线段,并给出证明;如果没有,也要说明理由. 科目:czsx 来源: 题型:解答题
 如图,AB是半圆的直径,AC⊥AB,AC=AB,在半圆上任取一点D,过点D作DE⊥CD,交直径AB于点E,BF⊥AB,交线段AD的延长线于点F,问图中除了AB=AC外,是否还有其他两条线段相等?如果有,指出这两条相等的线段,并给出证明;如果没有,也要说明理由.
如图,AB是半圆的直径,AC⊥AB,AC=AB,在半圆上任取一点D,过点D作DE⊥CD,交直径AB于点E,BF⊥AB,交线段AD的延长线于点F,问图中除了AB=AC外,是否还有其他两条线段相等?如果有,指出这两条相等的线段,并给出证明;如果没有,也要说明理由.科目:czsx 来源: 题型:解答题
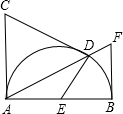
 如图,AB是半圆的直径,C是半圆弧上一点,CD⊥AB于D,
如图,AB是半圆的直径,C是半圆弧上一点,CD⊥AB于D, ,AB=10,求CD的长;
,AB=10,求CD的长;科目:czsx 来源:新课标九年级数学竞赛培训第21讲:三角形的内切圆(解析版) 题型:解答题
 是x°的弧,并要使点E在线段BA的延长线上,则x的取值范围是______;
是x°的弧,并要使点E在线段BA的延长线上,则x的取值范围是______;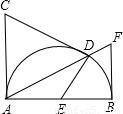
科目:czsx 来源:2009年浙江省温州市平阳中学提前自主招生选拔考试数学试卷(二)(解析版) 题型:解答题
科目:czsx 来源: 题型:
 如图,AB是半圆的直径,C是半圆弧上一点,CD⊥AB于D,
如图,AB是半圆的直径,C是半圆弧上一点,CD⊥AB于D,| 1 |
| 2 |
科目:gzsx 来源: 题型:
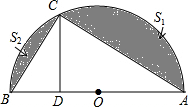
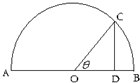 (1)(几何证明选讲)如图,AB是半圆O的直径,点C在半圆上,CD⊥AB,垂足为D,且AD=5DB,设∠COD=θ,则tanθ的值为
(1)(几何证明选讲)如图,AB是半圆O的直径,点C在半圆上,CD⊥AB,垂足为D,且AD=5DB,设∠COD=θ,则tanθ的值为
| ||
| 2 |
| ||
| 2 |
科目:gzsx 来源: 题型:解答题
 (1)(几何证明选讲)如图,AB是半圆O的直径,点C在半圆上,CD⊥AB,垂足为D,且AD=5DB,设∠COD=θ,则tanθ的值为________.
(1)(几何证明选讲)如图,AB是半圆O的直径,点C在半圆上,CD⊥AB,垂足为D,且AD=5DB,设∠COD=θ,则tanθ的值为________.科目:gzsx 来源:2012年陕西省西安市西工大附中高考数学四模试卷(理科)(解析版) 题型:解答题

科目:czsx 来源: 题型:
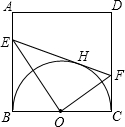 于E,交CD于F.
于E,交CD于F.| 13 | 48 |
科目:czsx 来源: 题型:解答题
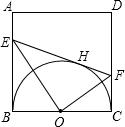 于E,交CD于F.
于E,交CD于F.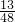 S,求BE与CF的长.
S,求BE与CF的长.科目:czsx 来源:增城市一模 题型:解答题

| 13 |
| 48 |
科目:czsx 来源:江苏期末题 题型:解答题
 ,求BE与CF的长。
,求BE与CF的长。
科目:czsx 来源:2008-2009学年江苏省镇江市丹阳实验初中九年级(上)期初数学试卷(解析版) 题型:解答题
 S,求BE与CF的长.
S,求BE与CF的长.
科目:czsx 来源:2008-2009学年江苏省苏州市高新区实验初中九年级(上)期末数学试卷(解析版) 题型:解答题
 S,求BE与CF的长.
S,求BE与CF的长.