点AB在X轴Y轴上OA=OB=3.是以AB为斜边的等腰答案解析
科目：czsx
来源：
题型：
如图，在平面直角坐标系中，直线
y=-x+b(b＞0)分别交x轴，y轴于A，B两点，以OA，OB为边作矩形OACB，D是直线BC上的动点，以M（2，0），N（12，0）为斜边端点作等腰直角三角形PMN，点P在第一象限．
（1）求直线AB过点P时b的值；
（2）在b的值变化过程中，若以P、B、D为顶点的三角形与△OAB相似，请求出所有符合条件的b的值；
（3）设矩形OACB与△PMN重叠部分的面积为S，当0＜b＜5时，求S与b的函数关系式．
查看答案和解析>>
科目：czsx
来源：
题型：
如图，点B的坐标为（0，8），C点的坐标为（0，10），AB⊥OB，OA=10，将△OAB绕点O按顺
时针方向旋转，使斜边OA落在x轴正半轴上，记作OAˊ，点B的落点Bˊ在第一象限．
（1）在给定的坐标系中画出△OA'B'，并求点A的坐标；
（2）求过C，A，A'三点的抛物线y=ax
2+bx+c的解析式；
（3）在（2）中的抛物线上是否存在点P，使以O、Aˊ、P为顶点的三角形是等腰直角三角形？若存在，求出所有的点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：czsx
来源：
题型：解答题
如图，点B的坐标为（0，8），C点的坐标为（0，10），AB⊥OB，OA=10，将△OAB绕点O按顺
时针方向旋转，使斜边OA落在x轴正半轴上，记作OAˊ，点B的落点Bˊ在第一象限．
（1）在给定的坐标系中画出△OA'B'，并求点A的坐标；
（2）求过C，A，A'三点的抛物线y=ax2+bx+c的解析式；
（3）在（2）中的抛物线上是否存在点P，使以O、Aˊ、P为顶点的三角形是等腰直角三角形？若存在，求出所有的点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：czsx
来源：2008年北京市通州区中考数学二模试卷（解析版）
题型：解答题
如图，点B的坐标为（0，8），C点的坐标为（0，10），AB⊥OB，OA=10，将△OAB绕点O按顺时针方向旋转，使斜边OA落在x轴正半轴上，记作OAˊ，点B的落点Bˊ在第一象限．
（1）在给定的坐标系中画出△OA'B'，并求点A的坐标；
（2）求过C，A，A'三点的抛物线y=ax
2+bx+c的解析式；
（3）在（2）中的抛物线上是否存在点P，使以O、Aˊ、P为顶点的三角形是等腰直角三角形？若存在，求出所有的点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：czsx
来源：2015届北京市门头沟区八年级下学期期末考试数学试卷（解析版）
题型：解答题
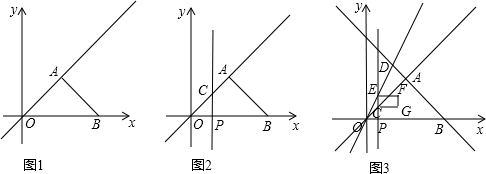
如图1，在平面直角坐标系xOy中，等腰直角△AOB的斜边OB在x上，顶点A的坐标为（3，3）.
（1）求直线OA的解析式；
（2）如图2，如果点P是x轴正半轴上的一个动点，过点P作PC∥y轴，交直线OA于点C，设点P的坐标为（m，0），以A、C、P、B为顶点的四边形面积为S，求S与m之间的函数关系式；
（3）如图3，如果点D（2，a）在直线AB上. 过点O、D作直线OD，交直线PC于点E，在CE的右侧作矩形CGFE，其中CG=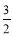
，请你直接写出矩形CGFE与△AOB重叠部分为轴对称图形时m的取值范围.
图1 图2 图3
查看答案和解析>>
科目：czsx
来源：
题型：
如图1，在平面直角坐标系xOy中，等腰直角△AOB的斜边OB在x上，顶点A的坐标为（3，3）．
（1）求直线OA的解析式；
（2）如图2，如果点P是x轴正半轴上的一个动点，过点P作PC∥y轴，交直线OA于点C，设点P的坐标为（m，0），以A、C、P、B为顶点的四边形面积为S，求S与m之间的函数关系式；
（3）如图3，如果点D（2，a）在直线AB上．过点O、D作直线OD，交直线PC于点E，在CE的右侧作矩形CGFE，其中CG=
，请你直接写出矩形CGFE与△AOB重叠部分为轴对称图形时m的取值范围．
查看答案和解析>>
科目：czsx
来源：
题型：
如图1，在平面直角坐标系xOy中，等腰直角△AOB的斜边OB在x上，顶点A的坐标为（3，3）.
（1）求直线OA的解析式；
（2）如图2，如果点P是x轴正半轴上的一个动点，过点P作PC∥y轴，交直线OA于点C，设点P的坐标为（m，0），以A、C、P、B为顶点的四边形面积为S，求S与m之间的函数关系式；
（3）如图3，如果点D（2，a）在直线AB上. 过点O、D作直线OD，交直线PC于点E，在CE的右侧作矩形CGFE，其中CG=
，请你直接写出矩形CGFE与△AOB重叠部分为轴对称图形时m的取值范围.
图1 图2 图3
查看答案和解析>>
科目：czsx
来源：
题型：
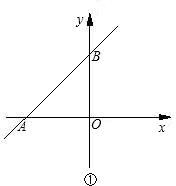
如图①，直线AB与x轴负半轴、y轴正半轴分别交于A、B两点．OA、OB的长度分别为a和b，且满足a
2-2ab+b
2=0．
（1）判断△AOB的形状．
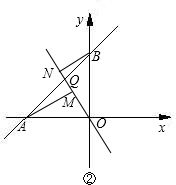
（2）如图②，正比例函数y=kx（k＜0）的图象与直线AB交于点Q，过A、B两点分别作AM⊥OQ于M，BN⊥OQ于N，若AM=9，BN=4，求MN的长．
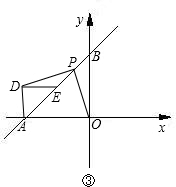
（3）如图③，E为AB上一动点，以AE为斜边作等腰直角△ADE，P为BE的中点，连接PD、PO，试问：线段PD、PO是否存在某种确定的数量关系和位置关系？写出你的结论并证明．
查看答案和解析>>
科目：czsx
来源：
题型：解答题
如图①，直线AB与x轴负半轴、y轴正半轴分别交于A、B两点．OA、OB的长度分别为a和b，且满足a2-2ab+b2=0．
（1）判断△AOB的形状．
（2）如图②，正比例函数y=kx（k＜0）的图象与直线AB交于点Q，过A、B两点分别作AM⊥OQ于M，BN⊥OQ于N，若AM=9，BN=4，求MN的长．
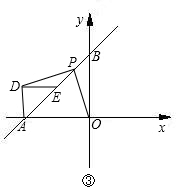
（3）如图③，E为AB上一动点，以AE为斜边作等腰直角△ADE，P为BE的中点，连接PD、PO，试问：线段PD、PO是否存在某种确定的数量关系和位置关系？写出你的结论并证明．
查看答案和解析>>
科目：czsx
来源：期末题
题型：解答题
如图①，直线AB与x轴负半轴、y轴正半轴分别交于A、B两点，OA、OB的长度分别为a和b，且满足 . |
| （1）判断△AOB的形状. |
|
|
（2）如图②，正比例函数 的图象与直线AB交于点Q，过A、B两点分别作AM⊥OQ于M，BN⊥OQ于N，若AM=9，BN=4，求MN的长. |
|
|
| （3）如图③，E为AB上一动点，以AE为斜边作等腰直角△ADE，P为BE的中点，连结PD、PO，试问：线段PD、PO是否存在某种确定的数量关系和位置关系？写出你的结论并证明. |
|
|
查看答案和解析>>
科目：czsx
来源：不详
题型：解答题
如图①，直线AB与x轴负半轴、y轴正半轴分别交于A、B两点．OA、OB的长度分别为a和b，且满足a
2-2ab+b
2=0．
（1）判断△AOB的形状．
（2）如图②，正比例函数y=kx（k＜0）的图象与直线AB交于点Q，过A、B两点分别作AM⊥OQ于M，BN⊥OQ于N，若AM=9，BN=4，求MN的长．
（3）如图③，E为AB上一动点，以AE为斜边作等腰直角△ADE，P为BE的中点，连接PD、PO，试问：线段PD、PO是否存在某种确定的数量关系和位置关系？写出你的结论并证明．
查看答案和解析>>
科目：czsx
来源：
题型：解答题
19．如图（1），直线AB与x轴负半轴、y轴的正半轴分别交于A、B、OA、OB的长分别为a、b，且满足a
2-2ab+b
2=0．
（1）判断△AOB的形状；
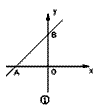
（2）如图（2）过坐标原点作直线OQ交直线AB于第二象限于点Q，过A、B两点分别作AM⊥OQ、BN⊥OQ，若AM=7，BN=4，求MN的长；
（3）如图（3），E为AB上一动点，以AE为斜边作等腰直角三角形ADE，P为BE的中点，延长DP至F，使PF=DP，连结PO，BF，试问DF、PO是否存在确定的位置关系和数量关系？写出你的结论并证明．
查看答案和解析>>
