
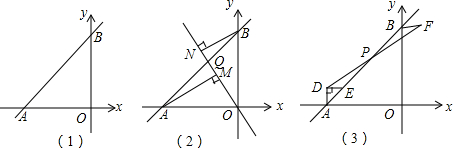
分析 (1)求出a=b,即可得出答案;
(2)求出∠AMO=∠ONB=90°,∠MAO=∠BON,根据AAS推出△AMO≌△ONB,根据全等得出ON=AM=7,OM=BN=4,即可求出答案;
(3)连接OD,OF,求出△BPF≌△EPD,根据全等得出BF=ED,∠FBP=∠DEP,求出BF=AD,∠FBO=∠DAO=90°,根据SAS推出△FBO≌△DAO,求出∠FOB=∠DOA,OD=OF,求出△DOF是等腰直角三角形,即可得出答案.
解答 (1)解:△AOB是等腰直角三角形,
理由是:∵a2-2ab+b2=0
(a-b)2=0,
∴a=b,
∴OA=OB
又∵∠AOB=90°,
∴△AOB是等腰直角三角形;
(2)解:∵AM⊥OQ,BN⊥OQ,
∴∠AMO=∠ONB=90°,
又∵∠AOB=90°,
∴∠AOM+∠BON=90°,
又∵∠MAO+∠MOA=90°,
∴∠MAO=∠BON,
在△AMO和△ONB中
$\left\{\begin{array}{l}{∠MAO=∠BON}\\{∠AMO=∠ONB}\\{AO=BO}\end{array}\right.$
∴△AMO≌△ONB(AAS),
∴ON=AM=7,OM=BN=4,
∴MN=ON-OM=7-4=3;
(3)OP=$\frac{1}{2}$DF且OP⊥DF,
证明:连接OD,OF,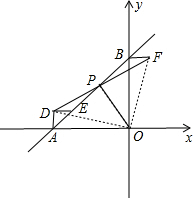
∵P为BE的中点,
∴BP=EP,
在△BPF和△EPD中
$\left\{\begin{array}{l}{BP=EP}\\{∠BPF=∠EPD}\\{PF=PD}\end{array}\right.$
∴△BPF≌△EPD(SAS)
∴BF=ED,∠FBP=∠DEP,
又∵△AED是等腰直角三角形,
∴AD=ED,∠DEA=∠DAE=45°,
∴BF=AD,
∴∠FBP=∠DEP=180°-45°=135°,
又∵△AOB和△ADE是等腰直角三角形,
∴OB=OA,∠DEA=∠DAE=45°,
∴BF=AD,
∴∠FBO=∠FBP-∠ABO=135°-45°=90°,
∠DAO=∠DAE+∠BAO=45°+45°=90°,
∴∠FBO=∠DAO=90°,
在△FBO和△DAO中
$\left\{\begin{array}{l}{BO=AO}\\{∠FBO=∠DAO}\\{BF=AD}\end{array}\right.$
∴△FBO≌△DAO(SAS)
∴∠FOB=∠DOA,OD=OF,
∴∠DOF=∠DOB+∠BOF=∠DOB+∠DOA=∠AOB=90°,
∴△DOF是等腰直角三角形,
又∵PF=DP,
∴OP=$\frac{1}{2}$DF,OP⊥DF.
点评 本题考查了全等三角形的性质和判定,坐标与图形性质,二元二次方程,等腰直角三角形的性质和判定的应用,能综合运用性质进行推理是解此题的关键,注意:全等三角形的对应边相等,对应角相等.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
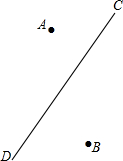 一辆货车在公路(直线CD)上由点C向点D方向行驶,村庄A、B分别位于道路CD的两侧,司机师傅要在公路上选择一个货物的下货点.
一辆货车在公路(直线CD)上由点C向点D方向行驶,村庄A、B分别位于道路CD的两侧,司机师傅要在公路上选择一个货物的下货点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ①④ | D. | ①③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com