科目:czsx 来源: 题型:解答题
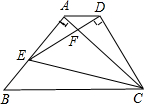
如图,在Rt△ABC中,∠BAC=90°,∠B=60°,BC=16cm,AD是斜边BC上的高,垂足为D,BE=1cm.点M从点B出发沿BC方向以1cm/s的速度运动,点N从点E出发,与点M同时同方向以相同的速度运动,以MN为边在BC的上方作正方形MNGH.点M到达点D时停止运动,点N到达点C时停止运动.设运动时间为t(s).
(1)当t为何值时,点G刚好落在线段AD上?
(2)设正方形MNGH与Rt△ABC重叠部分的图形的面积为S,当重叠部分的图形是正方形时,求出S关于t的函数关系式并写出自变量t的取值范围.
(3)设正方形MNGH的边NG所在直线与线段AC交于点P,连接DP,当t为何值时,△CPD是等腰三角形?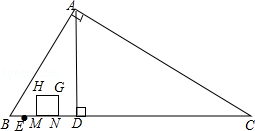
科目:czsx 来源:2014年初中毕业升学考试(湖南郴州卷)数学(解析版) 题型:解答题
如图,在Rt△ABC中,∠BAC=90°,∠B=60°,BC=16cm,AD是斜边BC上的高,垂足为D,BE=1cm.点M从点B出发沿BC方向以1cm/s的速度运动,点N从点E出发,与点M同时同方向以相同的速度运动,以MN为边在BC的上方作正方形MNGH.点M到达点D时停止运动,点N到达点C时停止运动.设运动时间为t(s).
(1)当t为何值时,点G刚好落在线段AD上?
(2)设正方形MNGH与Rt△ABC重叠部分的图形的面积为S,当重叠部分的图形是正方形时,求出S关于t的函数关系式并写出自变量t的取值范围.
(3)设正方形MNGH的边NG所在直线与线段AC交于点P,连接DP,当t为何值时,△CPD是等腰三角形?

科目:czsx 来源: 题型:单选题
科目:czsx 来源: 题型:
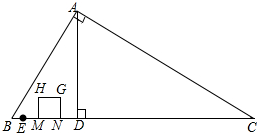 如图,在Rt△ABC中,∠BAC=90°,∠B=60°,BC=16cm,AD是斜边BC上的高,垂足为D,BE=1cm.点M从点B出发沿BC方向以1cm/s的速度运动,点N从点E出发,与点M同时同方向以相同的速度运动,以MN为边在BC的上方作正方形MNGH.点M到达点D时停止运动,点N到达点C时停止运动.设运动时间为t(s).
如图,在Rt△ABC中,∠BAC=90°,∠B=60°,BC=16cm,AD是斜边BC上的高,垂足为D,BE=1cm.点M从点B出发沿BC方向以1cm/s的速度运动,点N从点E出发,与点M同时同方向以相同的速度运动,以MN为边在BC的上方作正方形MNGH.点M到达点D时停止运动,点N到达点C时停止运动.设运动时间为t(s).科目:czsx 来源: 题型:解答题
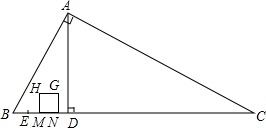 如图,在Rt△ABC中,∠BAC=90°,∠B=60°,BC=16cm,AD是斜边BC上的高,垂足为D,BE=1cm,点M从点B出发沿BC方向以1cm/s的速度运动,点N从点E出发,与点M同时同方向以相同速度运动,点N到达点C时停止运动,设运动时间为t(s).
如图,在Rt△ABC中,∠BAC=90°,∠B=60°,BC=16cm,AD是斜边BC上的高,垂足为D,BE=1cm,点M从点B出发沿BC方向以1cm/s的速度运动,点N从点E出发,与点M同时同方向以相同速度运动,点N到达点C时停止运动,设运动时间为t(s).科目:czsx 来源: 题型:
| A、两个相似三角形面积比为2:3,则周长比是4:9 | B、相似图形一定构成位似图形 | C、如果点D、E分别在△ABC的边AB、AC上,△ABC与△ADE相似,则DE∥BC | D、在Rt△ABC中,斜边上的高CD2=AD•BD |
科目:czsx 来源:不详 题型:单选题
| A.两个相似三角形面积比为2:3,则周长比是4:9 |
| B.相似图形一定构成位似图形 |
| C.如果点D、E分别在△ABC的边AB、AC上,△ABC与△ADE相似,则DE∥BC |
| D.在Rt△ABC中,斜边上的高CD2=AD•BD |
科目:czsx 来源: 题型:阅读理解
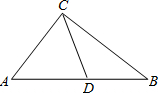 阅读:定理“直角三角形斜边上的中线等于斜边的一半”,如图,Rt△ABC中,D为AB中点,则CD=AD=BD=
阅读:定理“直角三角形斜边上的中线等于斜边的一半”,如图,Rt△ABC中,D为AB中点,则CD=AD=BD=| 1 | 2 |
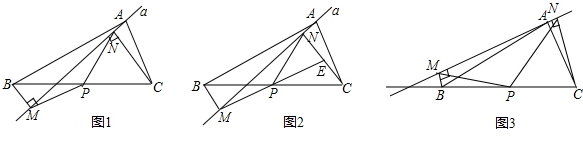
科目:czsx 来源: 题型:解答题
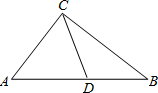 阅读:定理“直角三角形斜边上的中线等于斜边的一半”,如图,Rt△ABC中,D为AB中点,则CD=AD=BD=
阅读:定理“直角三角形斜边上的中线等于斜边的一半”,如图,Rt△ABC中,D为AB中点,则CD=AD=BD=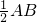 .(此定理在解决下面的问题中要用到)
.(此定理在解决下面的问题中要用到)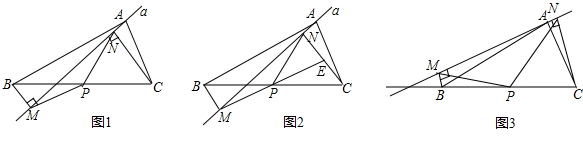
科目:czsx 来源:不详 题型:解答题
| 1 |
| 2 |


科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:解答题

科目:czsx 来源:江苏月考题 题型:解答题
科目:czsx 来源:江苏月考题 题型:解答题



科目:czsx 来源: 题型:
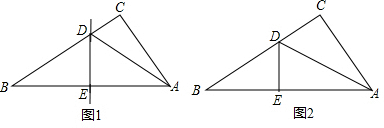
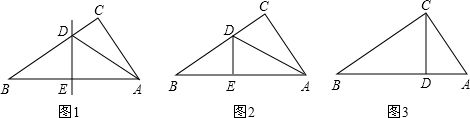
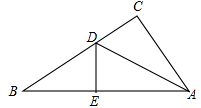
小丽剪了一些直角三角形纸片,她取出其中的几张进行了如下的操作:
操作一:如图,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.
⑴如果AC=6cm,BC=8cm,试求△ACD的周长.
⑵如果∠CAD:∠BAD=4:7,求∠B的度数.
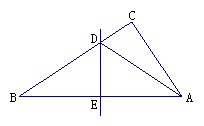
操作二:如图,小丽拿出另一张Rt△ABC纸片,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,已知两直角边AC=6cm,BC=8cm,你能求出CD的长吗?
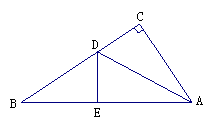
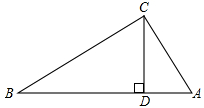
操作三:如图,小丽又拿出另一张Rt△ABC纸片,将纸片折叠,折痕CD⊥AB。
你能证明:BC2+AD2=AC2+BD2 吗?
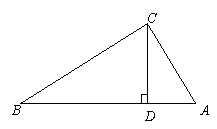 |
科目:czsx 来源:不详 题型:解答题

科目:czsx 来源:不详 题型:解答题

科目:czsx 来源: 题型:
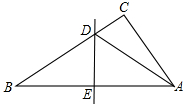
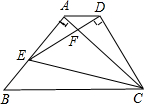 如图,△ABC为等腰直角三角形,∠BAC=90°,BC=2,E为AB上任意一动点,以CE为斜边作等腰Rt△CDE,连接AD,下列说法:①∠BCE=∠ACD;②AC⊥ED;③△AED∽△ECB;④AD∥BC;⑤四边形ABCD的面积有最大值,且最大值为
如图,△ABC为等腰直角三角形,∠BAC=90°,BC=2,E为AB上任意一动点,以CE为斜边作等腰Rt△CDE,连接AD,下列说法:①∠BCE=∠ACD;②AC⊥ED;③△AED∽△ECB;④AD∥BC;⑤四边形ABCD的面积有最大值,且最大值为| 3 |
| 2 |
| A、①②④ | B、①③⑤ |
| C、②③④ | D、①④⑤ |
科目:czsx 来源: 题型:单选题
如图,△ABC为等腰直角三角形,∠BAC=90°,BC=2,E为AB上任意一动点,以CE为斜边作等腰Rt△CDE,连接AD,下列说法:
①∠BCE=∠ACD;②AC⊥ED;③△AED∽△ECB;④AD∥BC;⑤四边形ABCD的面积有最大值,且最大值为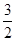 .其中,正确的结论是 。
.其中,正确的结论是 。
| A.①②④ | B.①③⑤ | C.②③④ | D.①④⑤ |