科目：czsx 来源： 题型：解答题
已知，如图直线AB与CD相交于点O，OE⊥AB，过点O作射线OF，∠AOD=30°，∠FOB=∠EOC．科目：czsx 来源： 题型：
如图，直线AB与CD相交于点O，OE⊥AB，OF⊥CD，OP是∠BOC的平分线．科目：czsx 来源：数学：5.1 相交线 同步练习(人教版七年级下) 人教版 题型：013
如图，直线AB与CD相交于点O，若∠AOC＝
∠AOD，则∠BOD的度数为
A．30°
B．45°
C．60°
D．135°
科目：czsx 来源：百分学生作业本课时3练1测 七年级数学(下) 适用人教课标版学生 人教课标版 题型：013
如图，直线AB、CD相交于点O，OE平分∠AOC，若∠AOD＝120°，则∠EOC的度数为________
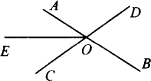
A．60°
B．45°
C．30°
D．120°
科目：czsx 来源：百分学生作业本课时3练1测 七年级数学(下) 适用人教课标版学生 人教课标版 题型：044
如图，直线AB、CD相交于点O，OE平分∠BOD，OF平分∠COE，∠AOD∶∠BOE＝4∶1，求∠AOF的度数．[方法提示：先由∠AOD∶∠BOE＝4∶1及∠BOE＝∠EOD和邻补角可求出∠BOE＝30°，∠AOD＝120°，再求∠COF．]
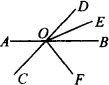
科目：czsx 来源： 题型：013
如图，直线AB、CD相交于点O，，OE⊥AB于点O，OF平分∠AOE，∠1=15°30′，则下列结论中不正确的是
[ ]
A．∠2=45°
B．∠1=∠3
C．∠AOD与∠1互为补角
D．∠1的余角等于75°30′
科目：czsx 来源：学习周报 数学 沪科九年级版 2009－2010学年 第16期 总第172期 沪科版 题型：013
如图，直线
AB与CD相交于点O，∠AOD＝30°，半径为1 cm的⊙P的圆心在射线OA上，且与点O的距离为6 cm．如果⊙P以1 cm/s的速度沿由A向B的方向移动，那么当⊙P与直线CD相切时，⊙P移动了
4 s
8 s
4 s或6 s
4 s或8 s
科目：czsx 来源： 题型：单选题
如图，直线AB与CD相交于点O，∠EOB=90°，∠FOD=90°，如果∠AOD=140°，那么∠EOF=科目：czsx 来源： 题型：单选题
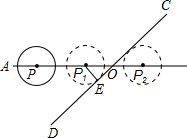如图，直线AB、CD相交于点O，∠AOD=30°，半径为1cm的⊙P的圆心在射线OA上，且与点O的距离为6cm．如果⊙P以1cm/s的速度沿由A向B的方向移动，那么秒钟后⊙P与直线CD相切．科目：czsx 来源：不详 题型：单选题
| A．4 | B．8 | C．4或6 | D．4或8 |
科目：czsx 来源：2011-2012学年辽宁省盘锦市四完中九年级（上）第四次月考数学试卷（解析版） 题型：选择题
科目：czsx 来源：2009-2010学年山东省济宁市邹城市九年级（上）期末数学试卷（解析版） 题型：选择题
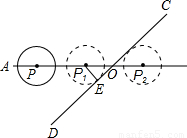
科目：czsx 来源：《24.2 与圆有关的位置关系》2010年同步学习检测（二）（解析版） 题型：选择题
科目：czsx 来源：不详 题型：解答题
科目：czsx 来源： 题型：
如图，直线AB、CD相交于点O，∠BOE=90°，OF平分∠AOE，∠1=15°30’，则下列结论不正确的是( )
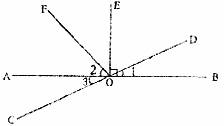
A．∠2=45° B．∠1=∠3
C．∠AOD+∠1=180° D．∠EOD=75°30’
已知：如图直线AB、CD相交于点O，OE平分∠AOD，∠FOC=90°，∠1=30°．求∠2和∠3的度数．
已知：如图直线AB、CD相交于点O，OE平分∠AOD，∠FOC=90°，∠1=30°．求∠2和∠3的度数．
如图，直线AB与CD相交于点O，OP是∠AOD的平分线，OF⊥CD，如果∠BOD=30°．
如图，直线AB与CD相交于点O，OP是∠AOD的平分线，OF⊥CD，如果∠BOD=30°．
如图，直线AB、CD相交于点O，EO⊥AB于点O，∠EOC=30°，则∠AOD的度数是（ ）