科目：czsx 来源： 题型：
| 1 |
| 2 |
科目：czsx 来源：2016届辽宁省丹东市中考模拟（四）数学试卷（解析版） 题型：解答题
已知：在Rt△ABC中，∠ABC=90°，∠C=60°，现将一个足够大的直角三角形的顶点P放在斜边AC上．
（1）设三角板的两直角边分别交边AB，BC于点M，N．
①当点P是AC的中点时，分别作PE⊥AB于点E，PF⊥BC于点F，得到图1，写出图中的一对全等三角形；
②在①的条件下，写出与△PEM相似的三角形，并直接写出PN与PM的数量关系．
（2）移动点P，使AP=2CP，将三角板绕点P旋转，设旋转过程中三角板的两直角边分别交边AB，BC于点M，N（PM不与边AB垂直，PN不与边BC垂直）；或者三角板的两直角边分别交边AB，BC的延长线于点M，N．
①请在备用图中画出图形，判断PM与PN的数量关系，并选择其中一种图形证明你的结论；
②在①的条件下，当△PCN是等腰三角形时，若BC=3cm，则线段BN的长是 ．
科目：czsx 来源：2016届辽宁省九年级上第四次质检数学试卷（解析版） 题型：解答题
已知：在Rt△ABC，∠ABC=90°，∠C=60°，现将一个足够大的直角三角板的顶点P放在斜边AC上．
（1）设三角板的两直角边分别交边AB、BC于点M、N．
①当点P是AC的中点时，分别作PE⊥AB于点E，PF⊥BC于点F，得到图1，写出图中的一对全等三角形；
②在①的条件下，写出与△PEM相似的三角形，并直接写出PN与PM的数量关系．
（2）移动点P，使AP=2CP，将三角板绕点P旋转，设旋转过程中三角板的两直角边分别交边AB、BC于点M、N（PM不与边AB垂直，PN不与边BC垂直）；或者三角板的两直角边分别交边AB、BC的延长线与点M、N．
③请在备用图中画出图形，判断PM与PN的数量关系，并选择其中一种图形证明你的结论；
④在③的条件下，当△PCN是等腰三角形时，若BC=3cm，则线段BN的长是 ．
科目：czsx 来源： 题型：解答题
科目：czsx 来源： 题型：
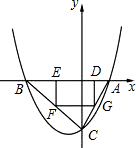如图，已知抛物线P：y=ax2+bx+c（a≠0）与x轴交于A、B两点（点A在x轴的正半轴上），与y轴交于点C，矩形DEFG的一条边DE在线段AB上，顶点F、G分别在线段BC、AC上，抛物线P上部分点的横坐标对应的纵坐标如下：| X | … | -3 | -2 | 1 | 2 | … | ||||
| y | … | -
|
-4 | -
|
0 | … |
科目：czsx 来源： 题型：
科目：czsx 来源：江苏省姜堰市2012届九年级上学期期中考试数学试题 题型：044
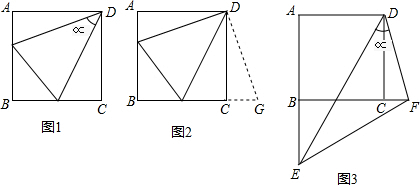
如图，已知正方形ABCD，将一个45度角∝的顶点放在D点并绕D点旋转，角的两边分别交AB边和BC边于点E和F，连接EF．求证：EF＝AE＋CF
(1)小明是这样思考的：延长BC到G，使得CG＝AE，连接DG，先证△DAE≌△DCG，再证△DEF≌△DGF，请你借助下图，按照小明的思路，写出完整的证明思路．
(2)刘老师看到这条题目后，问了小明两个小问题：①如果正方形的边长和△BEF的面积都等于6，求EF的长②将角∝绕D点继续旋转，使得角∝的两边分别和AB边延长线、BC边的延长线交于E和F，如图所示，猜想EF、AE、CF三线段之间的数量关系并给予证明．请你帮忙解决．
科目：czsx 来源： 题型：044
如图，已知抛物线P：y=ax2+bx+c(a≠0) 与x轴交于A、B两点(点A在x轴的正半轴上)，与y轴交于点C，矩形DEFG的一条边DE在线段AB上，顶点F、G分别在线段BC、AC上，抛物线P上部分点的横坐标对应的纵坐标如下：
|
x |
… |
-3 |
-2 |
1 |
2 |
… |
|
y |
… |
- |
-4 |
- |
0 |
… |
(1) 求A、B、C三点的坐标；
(2) 若点D的坐标为(m，0)，矩形DEFG的面积为S，求S与m的函数关系，并指出m的取值范围；
(3) 当矩形DEFG的面积S取最大值时，连接DF并延长至点M，使FM=k·DF，若点M不在抛物线P上，求k的取值范围.
若因为时间不够等方面的原因，经过探索、思考仍无法圆满解答本题，请不要轻易放弃，试试将上述(2)、(3)小题换为下列问题解答(已知条件及第(1)小题与上相同，完全正确解答只能得到5分)：
(2) 若点D的坐标为(1，0)，求矩形DEFG的面积.
科目：czsx 来源：2007年资阳市初中毕业升学统一考试、数学试卷 题型：059
如图，已知抛物线P：y＝ax2＋bx＋c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上)，与y轴交于点C，矩形DEFG的一条边DE在线段AB上，顶点F、G分别在线段BC、AC上，抛物线P上部分点的横坐标对应的纵坐标如下：
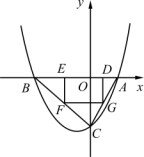
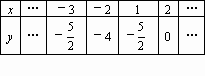
(1)求A、B、C三点的坐标；
(2)若点D的坐标为(m，0)，矩形DEFG的面积为S，求S与m的函数关系，并指出m的取值范围；
(3)当矩形DEFG的面积S取最大值时，连接DF并延长至点M，使FM＝k·DF，若点M不在抛物线P上，求k的取值范围．
若因为时间不够等方面的原因，经过探索、思考仍无法圆满解答本题，请不要轻易放弃，试试将上述(2)、(3)小题换为下列问题解答(已知条件及第(1)小题与上相同，完全正确解答只能得到5分)：
(2)若点D的坐标为(1，0)，求矩形DEFG的面积．
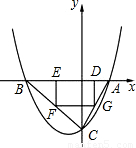
科目：czsx 来源：2009-2010学年九年级（上）期末综合试卷（1）（解析版） 题型：解答题
| X | … | -3 | -2 | 1 | 2 | … |
| y | … | - | -4 | - | … |
科目：czsx 来源：2009年浙江省宁波市中考数学模拟试卷（二）（解析版） 题型：解答题
| X | … | -3 | -2 | 1 | 2 | … |
| y | … | - | -4 | - | … |
科目：czsx 来源： 题型：解答题
科目：czsx 来源：不详 题型：解答题
科目：czsx 来源： 题型：
科目：czsx 来源：2012—2013学年江苏沭阳银河学校初三上第一次月考数学试卷（带解析） 题型：解答题
如图1，已知正方形ABCD，将一个45度角
的顶点放在D点并绕D点旋转，角的两边分别交AB边和BC边于点E和F，连接EF。求证：EF＝AE+CF
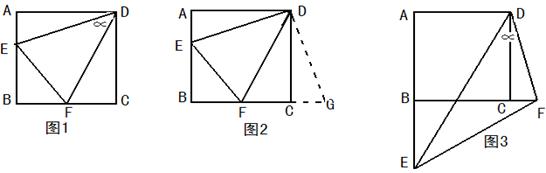（1） 小明是这样思考的:延长BC到G，使得CG＝AE，连接DG，先证△DAE≌△DCG，再证△DEF≌△DGF，请你借助图2，按照小明的思路，写出完整的证明思路。
（2）刘老师看到这条题目后，问了小明两个小问题：①如果正方形的边长和△BEF的面积都等于6，求EF的长；②将角绕D点继续旋转，使得角的两边分别和AB边延长线、BC边的延长线交于E和F，如图3所示，猜想EF、AE、CF三线段之间的数量关系并给予证明。请你帮忙解决。
已知线段AB，
