已知M(x.y)是平面直角坐标系xoy中的点.其中x是答案解析
科目:czsx
来源:
题型:
已知:如图,平面直角坐标系xOy中,点A、B的坐标分别为A(4,0),B(0,-4),P为y轴上
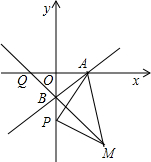
B点下方一点,PB=m(m>0),以AP为边作等腰直角三角形APM,其中PM=PA,点M落在第四象限.
(1)求直线AB的解析式;
(2)用m的代数式表示点M的坐标;
(3)若直线MB与x轴交于点Q,判断点Q的坐标是否随m的变化而变化,写出你的结论并说明理由.
查看答案和解析>>
科目:czsx
来源:北京期末题
题型:解答题
已知:如图,平面直角坐标系xOy中,点A、B的坐标分别为A(4,0),B(0,﹣4),P为y轴上B点下方一点,PB=m(m>0),以AP为边作等腰直角三角形APM,其中PM=PA,点M落在第四象限.
(1)求直线AB的解析式;
(2)用m的代数式表示点M的坐标;
(3)若直线MB与x轴交于点Q,判断点Q的坐标是否随m的变化而变化,写出你的结论并说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
10.对于平面直角坐标系 xOy中的点P(a,b),若点P′的坐标为($a+\frac{b}{k}$,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”. 例如:P(1,4)的“2属派生点”为P′(1+$\frac{4}{2}$,2×1+4),即P′(3,6).
(1)点P(-1,-2)的“2属派生点”P′的坐标为(-2,-4);
(2)若点P在x轴的正半轴上,点P的“k属派生点”为P'点,且△OPP′为等腰直角三角形,求k的值;
(3)已知点Q为二次函数$y={x^2}+4\sqrt{3}x+16$图象上的一动点,点A在函数$y=-\frac{{4\sqrt{3}}}{x}$(x<0)的图象上,且点A是点B的“$-\sqrt{3}$属派生点”,当线段B Q最短时,求Q点坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
在平面直角坐标系xOy中,已知二次函数y=ax
2+bx+c(a≠0)的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,其顶点的横坐标为1,且过点(2,3)和(-3,-12).
(1)求此二次函数的表达式;
(2)若直线l:y=kx(k≠0)与线段BC交于点D(不与点B,C重合),则是否存在这样的直线l,使得以B,O,D为顶点的三角形与△BAC相似?若存在,求出该直线的函数表达式及点D的坐标;若不存在,请说明理由;
(3)若点P是位于该二次函数对称轴右边图象上不与顶点重合的任意一点,试比较
锐角∠PCO与∠ACO的大小(不必证明),并写出此时点P的横坐标x
p的取值范围.
查看答案和解析>>
科目:czsx
来源:
题型:
在平面直角坐标系xOy中,已知直线l
1经过点A(-2,0)和点B(0,
),直线l
2的函数表达式为y=-
x+
,l
1与l
2相交于点P.⊙C是一个动圆,圆心C在直线l
1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.
(1)填空:直线l
1的函数表达式是
,交点P的坐标是
,∠FPB的度数是
°;
(2)当⊙C和直线l
2相切时,请证明点P到直线的距离CM等于⊙C的半径R,并写出R=
3-2时a的值;
(3)当⊙C和直线l
2不相离时,已知⊙C的半径R=
3-2,记四边形NMOB的面积为S(其中点N
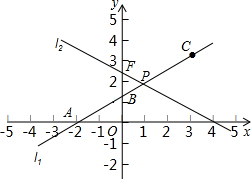
是直线CM与l
2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
在平面直角坐标系xOy中(如图),已知二次函数y=x
2+bx+c的图象经过点A(0,3)和点B(3,0),其顶点记为点C.
(1)确定此二次函数的解析式,并写出顶点C的坐标;
(2)将直线CB向上平移3个单位长度,求平移后直线l的解析式;
(3)在(2)的条件下,能否在直线上l找一点D,使得以点C、B、D、O为顶点的四边形是等腰梯形.若能,请求出点D的坐标;若不能,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
在平面直角坐标系xOy中,已知关于x的二次函数y=x
2+(k-1)x+2k-1的图象与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,其中k是一元二次方程p
2-p-2=0的根,且k<0.
(1)求这个二次函数的解析式及A、B两点的坐标;
(2)若直线l:y=mx(m≠0)与线段BC交于点D(点D不与点B、C重合),则是否存在这样的直线l,使得以B、O、D为顶点的三角形与△ABC相似?若存在,求出该直线的解析式及点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
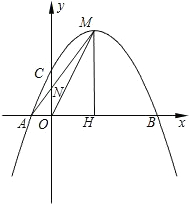
在平面直角坐标系xOy中,已知抛物线y=-
(x-2)2+c与x轴交于A、B两点(点A在点B的左侧),交y轴的正半轴于点C,其顶点为M,MH⊥x轴于点H,MA交y轴于点N,sin∠MOH=
.
(1)求此抛物线的函数表达式;
(2)过H的直线与y轴相交于点P,过O,M两点作直线PH的垂线,垂足分别为E,F,若
=
时,求点P的坐标;
(3)将(1)中的抛物线沿y轴折叠,使点A落在点D处,连接MD,Q为(1)中的抛物线上的一动点,直线NQ交x轴于点G,当Q点在抛物线上运动时,是否存在点Q,使△ANG与△ADM相似?若存在,求出所有符合条件的
直线QG的解析式;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
在平面直角坐标系xOy中,已知抛物线y=a(x+1)
2+c(a>0)与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,其顶点为M,若直线MC的函数表达式为y=kx-3,与x轴的交点为N,且cos∠BCO=
.
(1)求此抛物线的函数表达式;
(2)在此抛物线上是否存在异于点C的点P,使以N、P、C为顶点的三角形是以NC为一条直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;
(3)过点A作x轴的垂线,交直线MC于点Q.若将抛物线沿其对称轴上下平移,使抛物线与线段NQ总有公共点,则抛物线向上最多可平移多少个单位长度?向下最多可平移多少个单位长度?
查看答案和解析>>
科目:czsx
来源:
题型:
在平面直角坐标系xOy中,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,其顶点的横坐标为1,且过点(2,3)和(-3,-12).
(1)求此二次函数的表达式;
(2)若直线l:y=kx(k≠0)与线段BC交于点D(不与点B,C重合),则是否存在这样的直线l,使得△BOD∽△BAC?若存在,求出该直线的函数表达式及点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
在平面直角坐标系xOy中,抛物线y=-x
2+mx+n(m、n是常数)与x轴交于A、B两点,与y轴交于点C,经过B、C两点的直线的方程是y=x+2.
(1)求已知抛物线的解析式;
(2)将△ABC绕点A顺时针旋转90°得到△A′B′C′,求点C′的坐标;
(3)P是抛物线上的动点,当P在抛物线上从点B运动到点C,求P点纵坐标的取值范围.
(参考公式:抛物线y=ax
2+bx+c(其中a≠0)的顶点坐标为(-
,
))
查看答案和解析>>
科目:czsx
来源:
题型:

在平面直角坐标系xOy中,已知点P(3,4),点Q在x轴上,△PQO是等腰三角形,在图中标出满足条件的点Q位置,并写出其坐标.
查看答案和解析>>
科目:czsx
来源:
题型:044
在平面直角坐标系xOy中,已知直线l1经过点A(-2,0)和点B(0,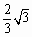 ),直线l2的函数表达式为
),直线l2的函数表达式为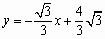 ,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.
,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.
(1)
填空:直线
l1的函数表达式是
▲ ,交点
P的坐标是
▲ ,∠
FPB的度数是
▲ ;
(2)
当⊙
C和直线
l2相切时,请证明点
P到直线
CM的距离等于⊙
C的半径
R,并写出
R=
时
a的值.
(3)
当⊙
C和直线
l2不相离时,已知⊙
C的半径
R=
,记四边形
NMOB的面积为
S(其中点
N是直线
CM与
l2的交点
).
S是否存在最大值?若存在,求出这个最大值及此时
a的值;若不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:新课程 新理念 新思维·训练编·数学 九年级下册(苏教版) 苏教版
题型:059
在平面直角坐标系xOy中,已知直线l1经过点A(-2,0)和点B(0, ),直线l2的函数表达式为=-
),直线l2的函数表达式为=- x+
x+ ,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.
,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.

(1)填空:直线l1的函数表达式是________,交点P的坐标是________,∠FPB的度数是________;
(2)当⊙C和直线l2相切时,请证明点P到直线CM的距离等于⊙C的半径R,并写出R= -2时a的值.
-2时a的值.
(3)当⊙C和直线l2不相离时,已知⊙C的半径R= -2,记四边形NMOB的面积为S(其中点N是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.
-2,记四边形NMOB的面积为S(其中点N是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:2007年成都市初中毕业、升学统一考试数学试卷
题型:044
在平面直角坐标系xOy中,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,其顶点的横坐标为1,且过点(2,3)和(-3,-12).

(1)求此二次函数的表达式;
(2)若直线l:y=kx(k≠0)与线段BC交于点D(不与点B,C重合),则是否存在这样的直线l,使得以B,O,D为顶点的三角形与△BAC相似?若存在,求出该直线的函数表达式及点D的坐标;若不存在,请说明理由;
(3)若点P是位于该二次函数对称轴右边图象上不与顶点重合的任意一点,试比较锐角∠PCO与∠ACO的大小(不必证明),并写出此时点P的横坐标xp的取值范围.
查看答案和解析>>
科目:czsx
来源:江苏省盐城市2012年中考数学试题
题型:044
在平面直角坐标系xOy中,已知二次函数y=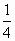 x2+mx+n的图象经过点A(2,0)和点B(1,-
x2+mx+n的图象经过点A(2,0)和点B(1,-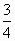 ),直线l经过抛物线的顶点且与y轴垂直,垂足为Q.
),直线l经过抛物线的顶点且与y轴垂直,垂足为Q.
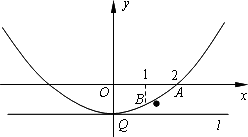
(1)求该二次函数的表达式;
(2)设抛物线上有一动点P从点B处出发沿抛物线向上运动,其纵坐标y1随时间t(t≥0)的变化规律为y1=- +2t.现以线段OP为直径作⊙C.
+2t.现以线段OP为直径作⊙C.
①当点P在起始位置点B处时,试判断直线l与⊙C的位置关系,并说明理由;在点P运动的过程中,直线l与⊙C是否始终保持这种位置关系?请说明你的理由;
②若在点P开始运动的同时,直线l也向上平行移动,且垂足Q的纵坐标y2随时间t的变化规律为y2=-1+3t,则当t在什么范围内变化时,直线l与⊙C相交?此时,若直线l被⊙C所截得的弦长为a,试求a2的最大值.

查看答案和解析>>
科目:czsx
来源:2006年浙江省初中毕业生学业考试数学试题
题型:059
在平面直角坐标系xOy中,已知直线l1经过点A(-2,0)和点B(0, ),直线l2的函数表达式为y=-
),直线l2的函数表达式为y=- x+
x+ ,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.
,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.

(1)填空:直线l1的函数表达式是________,交点P的坐标是________,∠FPB的度数是________;
(2)当⊙C和直线l2相切时,请证明点P到直线的距离CM等于⊙C的半径R,并写出R= 时a的值.
时a的值.
(3)当⊙C和直线l2不相离时,已知⊙C的半径R= ,记四边形NMOB的面积为S(其中点N是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.
,记四边形NMOB的面积为S(其中点N是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:苏科版(新课标) 九年级上册
题型:
|
|
|
在平面直角坐标系xOy中,已知点A(6,0),点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列),连接AB.
(1)当OC∥AB时,∠BOC的度数为________;
(2)连接AC,BC,当点C在⊙O上运动到什么位置时,△ABC的面积最大?并求出△ABC的面积的最大值.
(3)连接AD,当OC∥AD时,
①求出点C的坐标;
②直线BC是否为⊙O的切线?
请作出判断,并说明理由.

|
|
|
查看答案和解析>>
科目:czsx
来源:
题型:解答题
在平面直角坐标系xOy中,抛物线y=-x2+mx+n(m、n是常数)与x轴交于A、B两点,与y轴交于点C,经过B、C两点的直线的方程是y=x+2.
(1)求已知抛物线的解析式;
(2)将△ABC绕点A顺时针旋转90°得到△A′B′C′,求点C′的坐标;
(3)P是抛物线上的动点,当P在抛物线上从点B运动到点C,求P点纵坐标的取值范围.
(参考公式:抛物线y=ax2+bx+c(其中a≠0)的顶点坐标为(- ,
, ))
))
查看答案和解析>>
科目:czsx
来源:
题型:解答题
在平面直角坐标系xOy中,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,其顶点的横坐标为1,且过点(2,3)和(-3,-12).
(1)求此二次函数的表达式;
(2)若直线l:y=kx(k≠0)与线段BC交于点D(不与点B,C重合),则是否存在这样的直线l,使得△BOD∽△BAC?若存在,求出该直线的函数表达式及点D的坐标;若不存在,请说明理由.
查看答案和解析>>

 B点下方一点,PB=m(m>0),以AP为边作等腰直角三角形APM,其中PM=PA,点M落在第四象限.
B点下方一点,PB=m(m>0),以AP为边作等腰直角三角形APM,其中PM=PA,点M落在第四象限.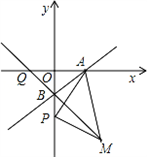
 锐角∠PCO与∠ACO的大小(不必证明),并写出此时点P的横坐标xp的取值范围.
锐角∠PCO与∠ACO的大小(不必证明),并写出此时点P的横坐标xp的取值范围.  是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.
是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.  在平面直角坐标系xOy中(如图),已知二次函数y=x2+bx+c的图象经过点A(0,3)和点B(3,0),其顶点记为点C.
在平面直角坐标系xOy中(如图),已知二次函数y=x2+bx+c的图象经过点A(0,3)和点B(3,0),其顶点记为点C. 在平面直角坐标系xOy中,已知关于x的二次函数y=x2+(k-1)x+2k-1的图象与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,其中k是一元二次方程p2-p-2=0的根,且k<0.
在平面直角坐标系xOy中,已知关于x的二次函数y=x2+(k-1)x+2k-1的图象与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,其中k是一元二次方程p2-p-2=0的根,且k<0. 直线QG的解析式;若不存在,请说明理由.
直线QG的解析式;若不存在,请说明理由. ![]() ),直线l2的函数表达式为
),直线l2的函数表达式为![]() ,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.
,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.
![]() ),直线l2的函数表达式为=-
),直线l2的函数表达式为=-![]() x+
x+![]() ,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.
,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.
![]() -2时a的值.
-2时a的值.![]() -2,记四边形NMOB的面积为S(其中点N是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.
-2,记四边形NMOB的面积为S(其中点N是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.

![]() x2+mx+n的图象经过点A(2,0)和点B(1,-
x2+mx+n的图象经过点A(2,0)和点B(1,-![]() ),直线l经过抛物线的顶点且与y轴垂直,垂足为Q.
),直线l经过抛物线的顶点且与y轴垂直,垂足为Q.
![]() +2t.现以线段OP为直径作⊙C.
+2t.现以线段OP为直径作⊙C.
![]() ),直线l2的函数表达式为y=-
),直线l2的函数表达式为y=-![]() x+
x+![]() ,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.
,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.
![]() 时a的值.
时a的值.![]() ,记四边形NMOB的面积为S(其中点N是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.
,记四边形NMOB的面积为S(其中点N是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.
 ,
, ))
))