科目:czsx
来源:2016届辽宁省丹东市九年级第一次月考数学试卷(解析版)
题型:解答题
探索证明(本题满分11分)如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AD,BD, BC,AC的中点.

(1)求证:四边形EFGH是平行四边形;
(2)当四边形ABCD满足一个什么条件时,四边形EFGH是菱形?并证明你的结论.
(3)当AB和CD满足什么条件时,四边形EFGH是正方形.(直接写出结论,不必写证明过程)
查看答案和解析>>
科目:czsx
来源:
题型:解答题
13.

如图,点E、F分别在直线AB、CD上,连接EF,分别作∠AEF、∠CFE的平分线交于点G,∠BEF、∠DFE的平分线交于点H,得到的四边形EFGH为矩形.
(1)求证:AB∥CD.
(2)小明在完成(1)的证明后继续进行了探索,过点G作MN∥EF,分别交AB、CD于点M、N,过点H作PQ∥EF,分别交AB、CD于点P、Q,得到四边形MNQP.此时,他猜想四边形MNQP是菱形.请补全他的证明思路.
小明的证明思路:
由AB∥CD,MN∥EF,PQ∥EF易证,四边形MNQP是平行四边形.要证▱MNQP是菱形,只要证MN=NQ.由已知条件FG平分∠CFE,MN∥EF,可得GN=FN,故只要证GM=FQ,即证△MGE≌△QFH,由于易证GE=FH,∠GME=∠FQH,故要证△MGE≌△QFH,只要证∠MGE=∠QFH,由∠MGE=∠GEF,∠QFH=∠EFH,∠GEF=∠EFH,即可得证.
(3)请你再写出一条菱形的判定定理.
查看答案和解析>>
科目:czsx
来源:
题型:
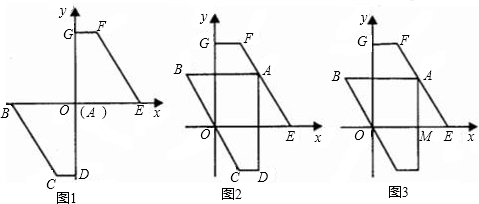
如图,直角梯形ABCD的腰BC所在直线的解析式为y=-
x-6
,点A与坐标原点O重合,点D的坐标为(0,-4
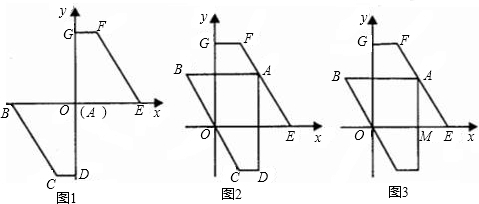
),将直角梯形ABCD绕点O顺时针旋转180°,得到直角梯形OEFG(如图1).
(1)直接写出E,F两点的坐标及直角梯形OEFG的腰EF所在直线的解析式;
(2)将图1中的直角梯形ABCD先沿x轴向右平移到点A与点E重合的位置,再让直角顶点A紧贴着EF,向上平移直角梯形ABCD(即梯形ABCD向上移动时,总保持着AB∥FG),当点A与点F重合时,梯形ABCD停止移动.观察得知:在梯形ABCD移动过程中,其腰BC始终经过坐标原点O.(如图2)
①设点A的坐标为(a,b),梯形ABCD与梯形OEFG重合部分的面积为S,试求a与何值时,S的值恰好等于梯形OEFG面积的
;
②当点A在EF上滑动时,设AD与x轴的交点为M,试问:在y轴上是否存在点P,使得△PAM是底角为30°的等腰三角形?如果存在,请求出所有符合条件的点P的坐标;如果不存在,请说明理由.(利用图3进行探索)
查看答案和解析>>
科目:czsx
来源:2007年全国中考数学试题汇编《一次函数》(06)(解析版)
题型:解答题
(2007•随州)如图,直角梯形ABCD的腰BC所在直线的解析式为y=-
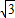
x-6
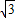
,点A与坐标原点O重合,点D的坐标为(0,-4
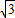
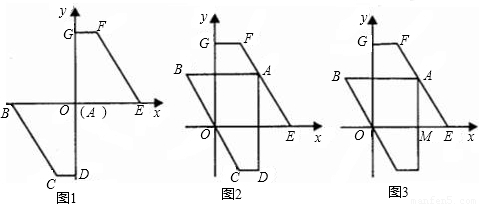
),将直角梯形ABCD绕点O顺时针旋转180°,得到直角梯形OEFG(如图1).
(1)直接写出E,F两点的坐标及直角梯形OEFG的腰EF所在直线的解析式;
(2)将图1中的直角梯形ABCD先沿x轴向右平移到点A与点E重合的位置,再让直角顶点A紧贴着EF,向上平移直角梯形ABCD(即梯形ABCD向上移动时,总保持着AB∥FG),当点A与点F重合时,梯形ABCD停止移动.观察得知:在梯形ABCD移动过程中,其腰BC始终经过坐标原点O.(如图2)
①设点A的坐标为(a,b),梯形ABCD与梯形OEFG重合部分的面积为S,试求a与何值时,S的值恰好等于梯形OEFG面积的
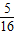
;
②当点A在EF上滑动时,设AD与x轴的交点为M,试问:在y轴上是否存在点P,使得△PAM是底角为30°的等腰三角形?如果存在,请求出所有符合条件的点P的坐标;如果不存在,请说明理由.(利用图3进行探索)
查看答案和解析>>
科目:czsx
来源:2007年湖北省随州市中考数学试卷(解析版)
题型:解答题
(2007•随州)如图,直角梯形ABCD的腰BC所在直线的解析式为y=-
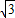
x-6
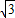
,点A与坐标原点O重合,点D的坐标为(0,-4
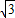
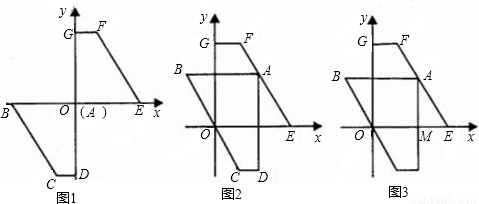
),将直角梯形ABCD绕点O顺时针旋转180°,得到直角梯形OEFG(如图1).
(1)直接写出E,F两点的坐标及直角梯形OEFG的腰EF所在直线的解析式;
(2)将图1中的直角梯形ABCD先沿x轴向右平移到点A与点E重合的位置,再让直角顶点A紧贴着EF,向上平移直角梯形ABCD(即梯形ABCD向上移动时,总保持着AB∥FG),当点A与点F重合时,梯形ABCD停止移动.观察得知:在梯形ABCD移动过程中,其腰BC始终经过坐标原点O.(如图2)
①设点A的坐标为(a,b),梯形ABCD与梯形OEFG重合部分的面积为S,试求a与何值时,S的值恰好等于梯形OEFG面积的
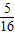
;
②当点A在EF上滑动时,设AD与x轴的交点为M,试问:在y轴上是否存在点P,使得△PAM是底角为30°的等腰三角形?如果存在,请求出所有符合条件的点P的坐标;如果不存在,请说明理由.(利用图3进行探索)
查看答案和解析>>
科目:czsx
来源:
题型:解答题
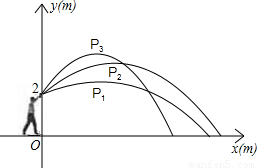
小明代表班级参加校运会的铅球项目,他想:“怎样才能将铅球推得更远呢”,于是找来小刚做了如下的探索:小明手挚铅球在控制每次推出时用力相同的条件下,分别沿与水平线成30°、45°、60°方向推了三次.铅球推出后沿抛物线形运动.如图,小明推铅球时的出手点距地面2m,以铅球出手点所在竖直方向为y轴、地平线为x轴建立直角坐标系,分别得到的有关数据如下表:
| 铅球的方向与水平线的夹角 | 300 | 450 | 600 |
| 铅球运行所得到的抛物线解析式 | y1=-0.06(x-3)2+2.5 | y2=
(x-4)2+3.6 | y3=-0.22(x-3)2+4 |
| 估测铅球在最高点的坐标 | P1(3,2.5) | P2(4,3.6) | P3(3,4) |
| 铅球落点到小明站立处的水平距离 | 9.5m |
m | 7.3m |
(1)请你求出表格中两横线上的数据,写出计算过程,并将结果填入表格中的横线上;
(2)请根据以上数据,对如何将铅球推得更远提出你的建议.

查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(24):2.6 何时获得最大利润(解析版)
题型:解答题
小明代表班级参加校运会的铅球项目,他想:“怎样才能将铅球推得更远呢”,于是找来小刚做了如下的探索:小明手挚铅球在控制每次推出时用力相同的条件下,分别沿与水平线成30°、45°、60°方向推了三次.铅球推出后沿抛物线形运动.如图,小明推铅球时的出手点距地面2m,以铅球出手点所在竖直方向为y轴、地平线为x轴建立直角坐标系,分别得到的有关数据如下表:
| 铅球的方向与水平线的夹角 | 30 | 45 | 60 |
| 铅球运行所得到的抛物线解析式 | y1=-0.06(x-3)2+2.5 | y2=
______(x-4)2+3.6 | y3=-0.22(x-3)2+4 |
| 估测铅球在最高点的坐标 | P1(3,2.5) | P2(4,3.6) | P3(3,4) |
| 铅球落点到小明站立处的水平距离 | 9.5m |
______m | 7.3m |
(1)请你求出表格中两横线上的数据,写出计算过程,并将结果填入表格中的横线上;
(2)请根据以上数据,对如何将铅球推得更远提出你的建议.

查看答案和解析>>
科目:czsx
来源:第34章《二次函数》中考题集(28):34.4 二次函数的应用(解析版)
题型:解答题
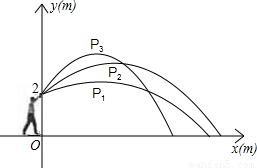
小明代表班级参加校运会的铅球项目,他想:“怎样才能将铅球推得更远呢”,于是找来小刚做了如下的探索:小明手挚铅球在控制每次推出时用力相同的条件下,分别沿与水平线成30°、45°、60°方向推了三次.铅球推出后沿抛物线形运动.如图,小明推铅球时的出手点距地面2m,以铅球出手点所在竖直方向为y轴、地平线为x轴建立直角坐标系,分别得到的有关数据如下表:
| 铅球的方向与水平线的夹角 | 30 | 45 | 60 |
| 铅球运行所得到的抛物线解析式 | y1=-0.06(x-3)2+2.5 | y2=
______(x-4)2+3.6 | y3=-0.22(x-3)2+4 |
| 估测铅球在最高点的坐标 | P1(3,2.5) | P2(4,3.6) | P3(3,4) |
| 铅球落点到小明站立处的水平距离 | 9.5m |
______m | 7.3m |
(1)请你求出表格中两横线上的数据,写出计算过程,并将结果填入表格中的横线上;
(2)请根据以上数据,对如何将铅球推得更远提出你的建议.
查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(27):2.3 二次函数的应用(解析版)
题型:解答题
小明代表班级参加校运会的铅球项目,他想:“怎样才能将铅球推得更远呢”,于是找来小刚做了如下的探索:小明手挚铅球在控制每次推出时用力相同的条件下,分别沿与水平线成30°、45°、60°方向推了三次.铅球推出后沿抛物线形运动.如图,小明推铅球时的出手点距地面2m,以铅球出手点所在竖直方向为y轴、地平线为x轴建立直角坐标系,分别得到的有关数据如下表:
| 铅球的方向与水平线的夹角 | 30 | 45 | 60 |
| 铅球运行所得到的抛物线解析式 | y1=-0.06(x-3)2+2.5 | y2=
______(x-4)2+3.6 | y3=-0.22(x-3)2+4 |
| 估测铅球在最高点的坐标 | P1(3,2.5) | P2(4,3.6) | P3(3,4) |
| 铅球落点到小明站立处的水平距离 | 9.5m |
______m | 7.3m |
(1)请你求出表格中两横线上的数据,写出计算过程,并将结果填入表格中的横线上;
(2)请根据以上数据,对如何将铅球推得更远提出你的建议.

查看答案和解析>>
科目:czsx
来源:第6章《二次函数》中考题集(27):6.4 二次函数的应用(解析版)
题型:解答题
小明代表班级参加校运会的铅球项目,他想:“怎样才能将铅球推得更远呢”,于是找来小刚做了如下的探索:小明手挚铅球在控制每次推出时用力相同的条件下,分别沿与水平线成30°、45°、60°方向推了三次.铅球推出后沿抛物线形运动.如图,小明推铅球时的出手点距地面2m,以铅球出手点所在竖直方向为y轴、地平线为x轴建立直角坐标系,分别得到的有关数据如下表:
| 铅球的方向与水平线的夹角 | 30 | 45 | 60 |
| 铅球运行所得到的抛物线解析式 | y1=-0.06(x-3)2+2.5 | y2=
______(x-4)2+3.6 | y3=-0.22(x-3)2+4 |
| 估测铅球在最高点的坐标 | P1(3,2.5) | P2(4,3.6) | P3(3,4) |
| 铅球落点到小明站立处的水平距离 | 9.5m |
______m | 7.3m |
(1)请你求出表格中两横线上的数据,写出计算过程,并将结果填入表格中的横线上;
(2)请根据以上数据,对如何将铅球推得更远提出你的建议.

查看答案和解析>>
科目:czsx
来源:《第27章 二次函数》2010年单元测试A卷(解析版)
题型:解答题
小明代表班级参加校运会的铅球项目,他想:“怎样才能将铅球推得更远呢”,于是找来小刚做了如下的探索:小明手挚铅球在控制每次推出时用力相同的条件下,分别沿与水平线成30°、45°、60°方向推了三次.铅球推出后沿抛物线形运动.如图,小明推铅球时的出手点距地面2m,以铅球出手点所在竖直方向为y轴、地平线为x轴建立直角坐标系,分别得到的有关数据如下表:
| 铅球的方向与水平线的夹角 | 30 | 45 | 60 |
| 铅球运行所得到的抛物线解析式 | y1=-0.06(x-3)2+2.5 | y2=
______(x-4)2+3.6 | y3=-0.22(x-3)2+4 |
| 估测铅球在最高点的坐标 | P1(3,2.5) | P2(4,3.6) | P3(3,4) |
| 铅球落点到小明站立处的水平距离 | 9.5m |
______m | 7.3m |
(1)请你求出表格中两横线上的数据,写出计算过程,并将结果填入表格中的横线上;
(2)请根据以上数据,对如何将铅球推得更远提出你的建议.

查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(29):2.8 二次函数的应用(解析版)
题型:解答题
小明代表班级参加校运会的铅球项目,他想:“怎样才能将铅球推得更远呢”,于是找来小刚做了如下的探索:小明手挚铅球在控制每次推出时用力相同的条件下,分别沿与水平线成30°、45°、60°方向推了三次.铅球推出后沿抛物线形运动.如图,小明推铅球时的出手点距地面2m,以铅球出手点所在竖直方向为y轴、地平线为x轴建立直角坐标系,分别得到的有关数据如下表:
| 铅球的方向与水平线的夹角 | 30 | 45 | 60 |
| 铅球运行所得到的抛物线解析式 | y1=-0.06(x-3)2+2.5 | y2=
______(x-4)2+3.6 | y3=-0.22(x-3)2+4 |
| 估测铅球在最高点的坐标 | P1(3,2.5) | P2(4,3.6) | P3(3,4) |
| 铅球落点到小明站立处的水平距离 | 9.5m |
______m | 7.3m |
(1)请你求出表格中两横线上的数据,写出计算过程,并将结果填入表格中的横线上;
(2)请根据以上数据,对如何将铅球推得更远提出你的建议.

查看答案和解析>>
科目:czsx
来源:第20章《二次函数和反比例函数》中考题集(25):20.5 二次函数的一些应用(解析版)
题型:解答题
小明代表班级参加校运会的铅球项目,他想:“怎样才能将铅球推得更远呢”,于是找来小刚做了如下的探索:小明手挚铅球在控制每次推出时用力相同的条件下,分别沿与水平线成30°、45°、60°方向推了三次.铅球推出后沿抛物线形运动.如图,小明推铅球时的出手点距地面2m,以铅球出手点所在竖直方向为y轴、地平线为x轴建立直角坐标系,分别得到的有关数据如下表:
| 铅球的方向与水平线的夹角 | 30 | 45 | 60 |
| 铅球运行所得到的抛物线解析式 | y1=-0.06(x-3)2+2.5 | y2=
______(x-4)2+3.6 | y3=-0.22(x-3)2+4 |
| 估测铅球在最高点的坐标 | P1(3,2.5) | P2(4,3.6) | P3(3,4) |
| 铅球落点到小明站立处的水平距离 | 9.5m |
______m | 7.3m |
(1)请你求出表格中两横线上的数据,写出计算过程,并将结果填入表格中的横线上;
(2)请根据以上数据,对如何将铅球推得更远提出你的建议.

查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(26):2.4 二次函数的应用(解析版)
题型:解答题
小明代表班级参加校运会的铅球项目,他想:“怎样才能将铅球推得更远呢”,于是找来小刚做了如下的探索:小明手挚铅球在控制每次推出时用力相同的条件下,分别沿与水平线成30°、45°、60°方向推了三次.铅球推出后沿抛物线形运动.如图,小明推铅球时的出手点距地面2m,以铅球出手点所在竖直方向为y轴、地平线为x轴建立直角坐标系,分别得到的有关数据如下表:
| 铅球的方向与水平线的夹角 | 30 | 45 | 60 |
| 铅球运行所得到的抛物线解析式 | y1=-0.06(x-3)2+2.5 | y2=
______(x-4)2+3.6 | y3=-0.22(x-3)2+4 |
| 估测铅球在最高点的坐标 | P1(3,2.5) | P2(4,3.6) | P3(3,4) |
| 铅球落点到小明站立处的水平距离 | 9.5m |
______m | 7.3m |
(1)请你求出表格中两横线上的数据,写出计算过程,并将结果填入表格中的横线上;
(2)请根据以上数据,对如何将铅球推得更远提出你的建议.
查看答案和解析>>
科目:czsx
来源:第23章《二次函数与反比例函数》中考题集(25):23.5 二次函数的应用(解析版)
题型:解答题
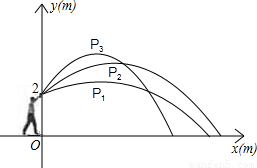
小明代表班级参加校运会的铅球项目,他想:“怎样才能将铅球推得更远呢”,于是找来小刚做了如下的探索:小明手挚铅球在控制每次推出时用力相同的条件下,分别沿与水平线成30°、45°、60°方向推了三次.铅球推出后沿抛物线形运动.如图,小明推铅球时的出手点距地面2m,以铅球出手点所在竖直方向为y轴、地平线为x轴建立直角坐标系,分别得到的有关数据如下表:
| 铅球的方向与水平线的夹角 | 30 | 45 | 60 |
| 铅球运行所得到的抛物线解析式 | y1=-0.06(x-3)2+2.5 | y2=
______(x-4)2+3.6 | y3=-0.22(x-3)2+4 |
| 估测铅球在最高点的坐标 | P1(3,2.5) | P2(4,3.6) | P3(3,4) |
| 铅球落点到小明站立处的水平距离 | 9.5m |
______m | 7.3m |
(1)请你求出表格中两横线上的数据,写出计算过程,并将结果填入表格中的横线上;
(2)请根据以上数据,对如何将铅球推得更远提出你的建议.
查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
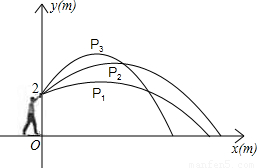
小明代表班级参加校运会的铅球项目,他想:“怎样才能将铅球推得更远呢”,于是找来小刚做了如下的探索:小明手挚铅球在控制每次推出时用力相同的条件下,分别沿与水平线成30°、45°、60°方向推了三次.铅球推出后沿抛物线形运动.如图,小明推铅球时的出手点距地面2m,以铅球出手点所在竖直方向为y轴、地平线为x轴建立直角坐标系,分别得到的有关数据如下表:
| 铅球的方向与水平线的夹角 | 300 | 450 | 600 |
| 铅球运行所得到的抛物线解析式 | y1=-0.06(x-3)2+2.5 | y2=
______(x-4)2+3.6 | y3=-0.22(x-3)2+4 |
| 估测铅球在最高点的坐标 | P1(3,2.5) | P2(4,3.6) | P3(3,4) |
| 铅球落点到小明站立处的水平距离 | 9.5m |
______m | 7.3m |
(1)请你求出表格中两横线上的数据,写出计算过程,并将结果填入表格中的横线上;
(2)请根据以上数据,对如何将铅球推得更远提出你的建议.

查看答案和解析>>
科目:czsx
来源:
题型:
小明代表班级参加校运会的铅球项目,他想:“怎样才能将铅球推得更远呢?”,于是找来小刚做了如下的探索:小明手挚铅球在控制每次推出时用力相同的条件下,分别沿与水平线成30°、45°、60°方向推了三次。铅球推出后沿抛物线形运动。如图,小明推铅球时的出手点距地面2m,以铅球出手点所在竖直方向为y轴、地平线为x轴建立直角坐标系,分别得到的有关数据如下表:
| 推铅球的方向与 水平线的夹角 | 30° | 45° | 60° |
| 铅球运行所得到 的抛物线解析式 |  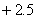
|  
| 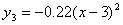 
|
| 估测铅球在 最高点的坐标 | P1(3,2.5) | P2(4,3.6) | P3(3,4) |
| 铅球落点到小明站 立处的水平距离 | 9.5m | ________m | 7.3m |

(1)请你求出表格中两横线上的数据,写出计算过程,并将结果填入表格中的横线上;
(2)请根据以上数据,对如何将铅球推得更远提出你的建议。
查看答案和解析>>
科目:czsx
来源:2005年全国中考数学试题汇编《二次函数》(05)(解析版)
题型:解答题
(2005•济南)小明代表班级参加校运会的铅球项目,他想:“怎样才能将铅球推得更远呢”,于是找来小刚做了如下的探索:小明手挚铅球在控制每次推出时用力相同的条件下,分别沿与水平线成30°、45°、60°方向推了三次.铅球推出后沿抛物线形运动.如图,小明推铅球时的出手点距地面2m,以铅球出手点所在竖直方向为y轴、地平线为x轴建立直角坐标系,分别得到的有关数据如下表:
| 铅球的方向与水平线的夹角 | 30 | 45 | 60 |
| 铅球运行所得到的抛物线解析式 | y1=-0.06(x-3)2+2.5 | y2=
______(x-4)2+3.6 | y3=-0.22(x-3)2+4 |
| 估测铅球在最高点的坐标 | P1(3,2.5) | P2(4,3.6) | P3(3,4) |
| 铅球落点到小明站立处的水平距离 | 9.5m |
______m | 7.3m |
(1)请你求出表格中两横线上的数据,写出计算过程,并将结果填入表格中的横线上;
(2)请根据以上数据,对如何将铅球推得更远提出你的建议.

查看答案和解析>>
科目:czsx
来源:2005年山东省济南市中考数学试卷(课标卷)(解析版)
题型:解答题
(2005•济南)小明代表班级参加校运会的铅球项目,他想:“怎样才能将铅球推得更远呢”,于是找来小刚做了如下的探索:小明手挚铅球在控制每次推出时用力相同的条件下,分别沿与水平线成30°、45°、60°方向推了三次.铅球推出后沿抛物线形运动.如图,小明推铅球时的出手点距地面2m,以铅球出手点所在竖直方向为y轴、地平线为x轴建立直角坐标系,分别得到的有关数据如下表:
| 铅球的方向与水平线的夹角 | 30 | 45 | 60 |
| 铅球运行所得到的抛物线解析式 | y1=-0.06(x-3)2+2.5 | y2=
______(x-4)2+3.6 | y3=-0.22(x-3)2+4 |
| 估测铅球在最高点的坐标 | P1(3,2.5) | P2(4,3.6) | P3(3,4) |
| 铅球落点到小明站立处的水平距离 | 9.5m |
______m | 7.3m |
(1)请你求出表格中两横线上的数据,写出计算过程,并将结果填入表格中的横线上;
(2)请根据以上数据,对如何将铅球推得更远提出你的建议.
查看答案和解析>>


 如图,点E、F分别在直线AB、CD上,连接EF,分别作∠AEF、∠CFE的平分线交于点G,∠BEF、∠DFE的平分线交于点H,得到的四边形EFGH为矩形.
如图,点E、F分别在直线AB、CD上,连接EF,分别作∠AEF、∠CFE的平分线交于点G,∠BEF、∠DFE的平分线交于点H,得到的四边形EFGH为矩形.
 x-6
x-6 ,点A与坐标原点O重合,点D的坐标为(0,-4
,点A与坐标原点O重合,点D的坐标为(0,-4 ),将直角梯形ABCD绕点O顺时针旋转180°,得到直角梯形OEFG(如图1).
),将直角梯形ABCD绕点O顺时针旋转180°,得到直角梯形OEFG(如图1). ;
;
 x-6
x-6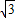 ,点A与坐标原点O重合,点D的坐标为(0,-4
,点A与坐标原点O重合,点D的坐标为(0,-4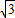 ),将直角梯形ABCD绕点O顺时针旋转180°,得到直角梯形OEFG(如图1).
),将直角梯形ABCD绕点O顺时针旋转180°,得到直角梯形OEFG(如图1).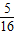 ;
;
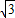 x-6
x-6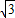 ,点A与坐标原点O重合,点D的坐标为(0,-4
,点A与坐标原点O重合,点D的坐标为(0,-4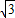 ),将直角梯形ABCD绕点O顺时针旋转180°,得到直角梯形OEFG(如图1).
),将直角梯形ABCD绕点O顺时针旋转180°,得到直角梯形OEFG(如图1).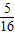 ;
;













