如图.将一副直角三角尺的直角顶点c叠放在一起.如图一答案解析
科目:czsx
来源:
题型:解答题
 将一副三角尺的两个直角顶点O重合在一起,如图那样摆放.
将一副三角尺的两个直角顶点O重合在一起,如图那样摆放.
(1)如果重叠在一起时,∠BOC=70°,则∠AOD=______度;
(2)如果重叠在一起时,∠BOC=50°,则∠AOD=______度;
(3)请猜想:不论旋转道何种位置,只要重叠在一起(重叠部分的角度大于0°且小于90°),∠BOC和∠AOD的和始终等于______度,并试说明理由.
查看答案和解析>>
科目:czsx
来源:期末题
题型:解答题
将一副三角尺的两个直角顶点O重合在一起,如图那样摆放.
(1)如果重叠在一起时,∠BOC=70°,则∠AOD= _________ 度;
(2)如果重叠在一起时,∠BOC=50°,则∠AOD= _________ 度;
(3)请猜想:不论旋转到何种位置,只要重叠在一起(重叠部分的角度大于0°且小于90°),∠BOC和∠AOD的和始终等于 _________ 度,并试说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:

25、将一副三角尺的两个直角顶点O重合在一起,如图那样摆放.
(1)如果重叠在一起时,∠BOC=70°,则∠AOD=
110
度;
(2)如果重叠在一起时,∠BOC=50°,则∠AOD=
130
度;
(3)请猜想:不论旋转道何种位置,只要重叠在一起(重叠部分的角度大于0°且小于90°),∠BOC和∠AOD的和始终等于
180
度,并试说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
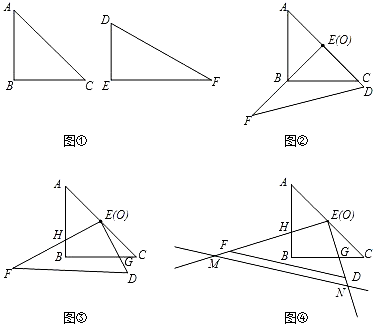
如图①是一副三角板,其中∠B=∠E=90°,∠A=∠C=45°,∠F=30°,AC=EF=2.把两个三角板ABC和DEF叠放在一起(如图②),且使三角板DEF的直角顶点E与三角板ABC的斜边中点O重合,DE和OC重合.现将三角板DEF绕O点顺时针旋转(旋转角α满足条件:0°<α<90°),四边形BGEH是旋转过程中两三角板的重叠部分(如图③).
(1)当旋转角度为45°时,EG和AB之间的数量关系为______.
(2)当DF经过三角板ABC的顶点B,求旋转角α的度数.
(3)在三角板DEF绕O点旋转的过程中,在DF上是否存在一点P,使得∠APC=90°,若存在,请利用直尺和圆规在DF上画出这个点,并说明理由,若不存在,请说明理由.
(4)在射线EF上取一点M,过M作DF的平行线交射线ED于点N(如图④),若直线MN上始终存在两个点P、Q,使得∠APC=∠AQC=90°,求EM的取值范围.
查看答案和解析>>
科目:czsx
来源:2009年江苏省南京市鼓楼区中考数学二模试卷(解析版)
题型:解答题
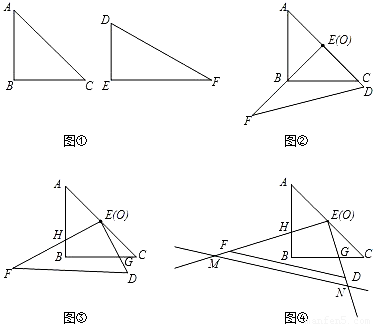
如图①是一副三角板,其中∠B=∠E=90°,∠A=∠C=45°,∠F=30°,AC=EF=2.把两个三角板ABC和DEF叠放在一起(如图②),且使三角板DEF的直角顶点E与三角板ABC的斜边中点O重合,DE和OC重合.现将三角板DEF绕O点顺时针旋转(旋转角α满足条件:0°<α<90°),四边形BGEH是旋转过程中两三角板的重叠部分(如图③).
(1)当旋转角度为45°时,EG和AB之间的数量关系为______.
(2)当DF经过三角板ABC的顶点B,求旋转角α的度数.
(3)在三角板DEF绕O点旋转的过程中,在DF上是否存在一点P,使得∠APC=90°,若存在,请利用直尺和圆规在DF上画出这个点,并说明理由,若不存在,请说明理由.
(4)在射线EF上取一点M,过M作DF的平行线交射线ED于点N(如图④),若直线MN上始终存在两个点P、Q,使得∠APC=∠AQC=90°,求EM的取值范围.
查看答案和解析>>
科目:czsx
来源:
题型:
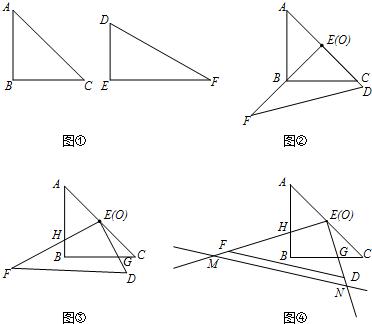
28、如图①是一副三角板,其中∠B=∠E=90°,∠A=∠C=45°,∠F=30°,AC=EF=2.把两个三角板ABC和DEF叠放在一起(如图②),且使三角板DEF的直角顶点E与三角板ABC的斜边中点O重合,DE和OC重合.现将三角板DEF绕O点顺时针旋转(旋转角α满足条件:0°<α<90°),四边形BGEH是旋转过程中两三角板的重叠部分(如图③).
(1)当旋转角度为45°时,EG和AB之间的数量关系为
AB=2EG
.
(2)当DF经过三角板ABC的顶点B,求旋转角α的度数.
(3)在三角板DEF绕O点旋转的过程中,在DF上是否存在一点P,使得∠APC=90°,若存在,请利用直尺和圆规在DF上画出这个点,并说明理由,若不存在,请说明理由.
(4)在射线EF上取一点M,过M作DF的平行线交射线ED于点N(如图④),若直线MN上始终存在两个点P、Q,使得∠APC=∠AQC=90°,求EM的取值范围.
查看答案和解析>>
科目:czsx
来源:
题型:
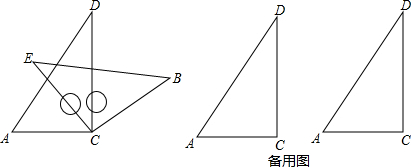
将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°):
(1)①若∠DCE=45°,则∠ACB的度数为
135°
135°
;
②若∠ACB=140°,求∠DCE的度数;
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(不必说明理由);若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起:

(1)若∠DCE=35°,则∠ACB的度数为 ▲ °;
(2)若∠ACB=140°,则∠DCE的度数为 ▲ °;
(3)∠ACB与∠DCE有怎样的数量关系?
(4)三角尺ACD不动,将三角尺BCE的CE边与CA边重合,然后绕点C按顺时针或逆时针方向任意转动一个角度,当∠ACE(0°<∠ACE<90°)等于多少度时,这两块三角尺各有一条边互相垂直,直接写出∠ACE角度所有可能的值,不用说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
将一副三角板中的两块直角三角尺的直角顶点
C按如图方式叠放在一起:

(1)若∠
DCE=35°,则∠
ACB的度数为
▲ °;
(2)若∠
ACB=140°,则∠
DCE的度数为
▲ °;
(3)∠
ACB与∠
DCE有怎样的数量关系?
(4)三角尺
ACD不动,将三角尺
BCE的
CE边与
CA边重合,然后绕点
C按顺时针或逆时针方向任意转动一个角度,当∠
ACE(0°<∠
ACE<90°)等于多少度时,这两块三角尺各有一条边互相垂直,直接写出∠
ACE角度所有可能的值,不用说明理由.
查看答案和解析>>
科目:czsx
来源:2010-2011学年江苏南京市第三初级中学七年级上学期期末考试数学卷(带解析)
题型:解答题
将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起:

(1)若∠DCE=35°,则∠ACB的度数为 ▲ °;
(2)若∠ACB=140°,则∠DCE的度数为 ▲ °;
(3)∠ACB与∠DCE有怎样的数量关系?
(4)三角尺ACD不动,将三角尺BCE的CE边与CA边重合,然后绕点C按顺时针或逆时针方向任意转动一个角度,当∠ACE(0°<∠ACE<90°)等于多少度时,这两块三角尺各有一条边互相垂直,直接写出∠ACE角度所有可能的值,不用说明理由.
查看答案和解析>>
科目:czsx
来源:2013届江苏南京市七年级上学期期末考试数学卷(解析版)
题型:解答题
将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起:
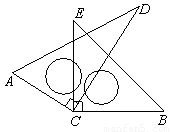
(1)若∠DCE=35°,则∠ACB的度数为 ▲ °;
(2)若∠ACB=140°,则∠DCE的度数为 ▲ °;
(3)∠ACB与∠DCE有怎样的数量关系?
(4)三角尺ACD不动,将三角尺BCE的CE边与CA边重合,然后绕点C按顺时针或逆时针方向任意转动一个角度,当∠ACE(0°<∠ACE<90°)等于多少度时,这两块三角尺各有一条边互相垂直,直接写出∠ACE角度所有可能的值,不用说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起:
将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起:
(1)若∠DCE=35°,则∠ACB的度数为______;
(2)若∠ACB=140°,求∠DCE的度数;
(3)猜想∠ACB与∠DCE的大小关系,并说明理由;
(4)三角尺ACD不动,将三角尺BCE的CE边与CA边重合,然后绕点C按顺时针或逆时针.方向任意转动一个角度,当∠ACE(0°<∠ACE<90°)等于多少度时,这两块三角尺各有一条边互相垂直,直接写出∠ACE角度所有可能的值,不用说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°):
(1)①若∠DCE=45°,则∠ACB的度数为______;
②若∠ACB=140°,求∠DCE的度数;
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(不必说明理由);若不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°):
(1)①若∠DCE=45°,则∠ACB的度数为______;
②若∠ACB=140°,求∠DCE的度数;
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(不必说明理由);若不存在,请说明理由.

查看答案和解析>>
科目:czsx
来源:
题型:
将一副三角板中 的两块直角三角尺的直
的两块直角三角尺的直 角顶点C按如图方式叠放在一起:
角顶点C按如图方式叠放在一起:
(1)若∠DCE=35°,则∠ACB的度数为 °;
(2)若∠ACB=140°,则∠DCE的度数为 °;
(3)∠ACB与∠DCE有怎样的数量关系?
(4)三角尺ACD不动,将三角尺BCE的CE边与CA边重合,然后绕点C按顺时针或逆时针方向任意转动一个角度,当∠ACE(0°<∠ACE<90°)等于多少度时,这两块三角尺各有一条边互相垂直,直接写出∠ACE角度所有可能的值,不用说明理由.

查看答案和解析>>
科目:czsx
来源:
题型:
将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起.

(1)如果∠DCE=36°,则∠ACB的度数为
;
(2)写出图中相等的角.如果∠DCE≠36°,它们还会相等吗?
(3)若∠DCE变小,∠ACB如何变化?
(4)在下图中利用能够画直角的工具再画一个与∠DCB相等的角.
查看答案和解析>>
科目:czsx
来源:
题型:
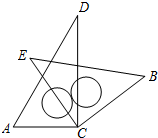
将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,
∠A=60°,∠D=30°;∠E=∠B=45°)
(1)若∠DCE=40°,则∠ACB的度数为
;
(2)若点E在AC的上方,设∠ACB=α(90°<α<180°),求∠DCE.(用含α的式子表示)
(3)请你动手操作,现将三角尺ACD固定,三角尺BCE的CE边与CA边重合,绕点C按顺时针方向任意转动一个角度,若0°<∠DCB<180°且点E在直线AC的上方,当这两块三角尺有一组边互相平行时,直接写出此时∠DCB角度所有可能的值(不必说明理由).
查看答案和解析>>
科目:czsx
来源:
题型:

23、将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起:
(1)若∠DCE=35°,则∠ACB的度数为
145°
;
(2)若∠ACB=140°,求∠DCE的度数;
(3)猜想∠ACB与∠DCE的大小关系,并说明理由;
(4)三角尺ACD不动,将三角尺BCE的CE边与CA边重合,然后绕点C按顺时针或逆时针.方向任意转动一个角度,当∠ACE(0°<∠ACE<90°)等于多少度时,这两块三角尺各有一条边互相垂直,直接写出∠ACE角度所有可能的值,不用说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
3.将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起.
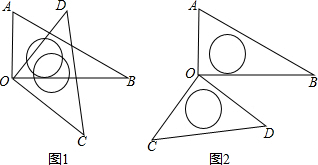
(1)如图(1)若∠BOD=35°,则∠AOC=145°;若∠AOC=135°,则∠BOD=45°;
(2)如图(2)若∠AOC=140°,则∠BOD=40°;
(3)猜想∠AOC与∠BOD的大小关系,并结合图(1)说明理由.
(4)三角尺AOB不动,将三角尺COD的OD边与OA边重合,然后绕点O按顺时针或逆时针方向任意转动一个角度,当∠AOD(0°<∠AOD<90°)等于多少度时,这两块三角尺各有一条边互相垂直,直接写出∠AOD角度所有可能的值,不用说明理由.
查看答案和解析>>
科目:czsx
来源:2014-2015学年江苏省七年级上学期期末考试数学试卷(解析版)
题型:解答题
(本题满分12分)如图1,小明将一副直角三角尺的直角顶点C叠放在一起.若保持三角尺BCE(其中∠EBC=45°)不动,三角尺ACD的CD边与CB边重合,然后将三角尺ACD(其中
∠ADC=30°)绕点C按逆时针方向任意转动一个角度∠BCD.
(1)如图2,若∠ECD =25°,则∠ACB= ;若∠ACB=130°,则∠ECD = .
(2)①当三角尺ACD绕直角顶点C旋转到如图2的位置时,猜想∠ACB与∠DCE的数量关系为 ;
②当三角尺ACD绕直角顶点C旋转到如图3的位置时,上述关系是否依然成立,请说明理由.
(3)设∠BCD=α(0°<α<180°)
①∠ACB能否是∠DCE的4倍?若能求出α的值;若不能说明理由.
②在旋转过程中,若AD与三角尺BCE的一条边平行,请求出α的所有可能值.



查看答案和解析>>

 将一副三角尺的两个直角顶点O重合在一起,如图那样摆放.
将一副三角尺的两个直角顶点O重合在一起,如图那样摆放.
 25、将一副三角尺的两个直角顶点O重合在一起,如图那样摆放.
25、将一副三角尺的两个直角顶点O重合在一起,如图那样摆放.







 将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起:
将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起:

![]() 的两块直角三角尺的直
的两块直角三角尺的直![]() 角顶点C按如图方式叠放在一起:
角顶点C按如图方式叠放在一起:

 将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,
将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中, 23、将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起:
23、将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起:


