
科目:gzsx 来源: 题型:解答题
 .
.科目:gzsx 来源: 题型:

科目:gzsx 来源: 题型:
| 3 | 5 |
科目:gzsx 来源: 题型:
 如图,△ABD是一直角边为1的直角等腰三角形,平面图形OBD是四分之一圆的扇形,点P在线段AB上,PQ⊥AB,且PQ交AD或交弧DB于点Q,设AP=x(0<x<2),图中阴影部分这平面图形APQ(或APQD)的面积为y,则函数y=f(x)的大致图象是( )
如图,△ABD是一直角边为1的直角等腰三角形,平面图形OBD是四分之一圆的扇形,点P在线段AB上,PQ⊥AB,且PQ交AD或交弧DB于点Q,设AP=x(0<x<2),图中阴影部分这平面图形APQ(或APQD)的面积为y,则函数y=f(x)的大致图象是( )A、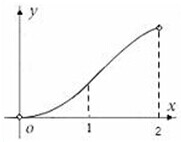 |
B、 |
C、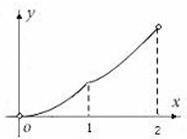 |
D、 |
科目:gzsx 来源:2010年扬州中学高一下学期期末考试数学 题型:解答题
(本小题满分16分) 一个三角形数表按如下方式构成:第一行依次写上n(n≥4)个数,在上一行的每相邻两数的中间正下方写上这两数之和,得到下一行,依此类推.记数表中第i行的第j个数为f(i,j).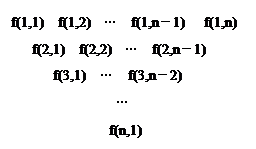
(1)若数表中第i (1≤i≤n-3)行的数依次成等差数列,求证:第i+1行的数也依次成等差数列;
(2)已知f(1,j)=4j,求f(i,1)关于i的表达式;
(3)在(2)的条件下,若f(i,1)=(i+1)(ai-1),bi= ,试求一个函数g(x),使得
Sn=b1g(1)+b2g(2)+…+bng(n)<,且对于任意的m∈(,),均存在实数,使得当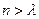 时,都有Sn >m.
时,都有Sn >m.
科目:gzsx 来源:2010年扬州中学高一下学期期末考试数学 题型:解答题
(本小题满分16分) 一个三角形数表按如下方式构成:第一行依次写上n(n≥4)个数,在上一行的每相邻两数的中间正下方写上这两数之和,得到下一行,依此类推.记数表中第i行的第j个数为f(i,j).
(1)若数表中第i (1≤i≤n-3)行的数依次成等差数列,求证:第i+1行的数也依次成等差数列;
(2)已知f(1,j)=4j,求f(i,1)关于i的表达式;
(3)在(2)的条件下,若f(i,1)=(i+1)(ai-1),bi= ,试求一个函数g(x),使得
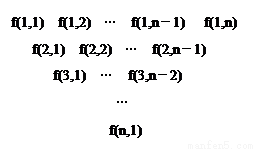 Sn=b1g(1)+b2g(2)+…+bng(n)<,且对于任意的m∈(,),均存在实数,使得当
Sn=b1g(1)+b2g(2)+…+bng(n)<,且对于任意的m∈(,),均存在实数,使得当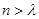 时,都有Sn >m.
时,都有Sn >m.
科目:gzsx 来源: 题型:
(本小题满分16分) 一个三角形数表按如下方式构成:第一行依次写上n(n≥4)个数,在上一行的每相邻两数的中间正下方写上这两数之和,得到下一行,依此类推.记数表中第i行的第j个数为f(i,j).
(1)若数表中第i (1≤i≤n-3)行的数依次成等差数列,求证:第i+1行的数也依次成等差数列;
(2)已知f(1,j)=4j,求f(i,1)关于i的表达式;
(3)在(2)的条件下,若f(i,1)=(i+1)(ai-1),bi= ,试求一个函数g(x),使得
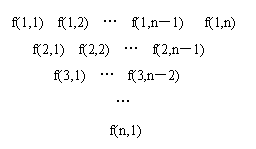 Sn=b1g(1)+b2g(2)+…+bng(n)<,且对于任意的m∈(,),均存在实数,使得当n>时,都有Sn >m.
Sn=b1g(1)+b2g(2)+…+bng(n)<,且对于任意的m∈(,),均存在实数,使得当n>时,都有Sn >m.
科目:gzsx 来源: 题型:
(本小题满分16分) 一个三角形数表按如下方式构成:第一行依次写上n(n≥4)个数,在上一行的每相邻两数的中间正下方写上这两数之和,得到下一行,依此类推.记数表中第i行的第j个数为f(i,j).
(1)若数表中第i (1≤i≤n-3)行的数依次成等差数列,求证:第i+1行的数也依次成等差数列;
(2)已知f(1,j)=4j,求f(i,1)关于i的表达式;
(3)在(2)的条件下,若f(i,1)=(i+1)(ai-1),bi= ,试求一个函数g(x),使得
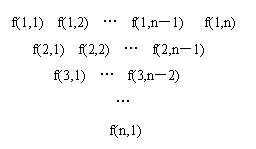 Sn=b1g(1)+b2g(2)+…+bng(n)<,且对于任意的m∈(,),均存在实数,使得当n>时,都有Sn >m.
Sn=b1g(1)+b2g(2)+…+bng(n)<,且对于任意的m∈(,),均存在实数,使得当n>时,都有Sn >m.
科目:gzsx 来源:不详 题型:解答题

 时,都有Sn >m.
时,都有Sn >m.科目:gzsx 来源: 题型:

科目:gzsx 来源: 题型:
| 产品编号 | A1 | A2 | A3 | A4 | A5 |
| 质量指标(x,y,z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
| 产品编号 | A6 | A7 | A8 | A9 | A10 |
| 质量指标(x,y,z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
科目:gzsx 来源: 题型:
| 月份 | 用水量(立方米) | 水费(元) |
| 一 | 5 | 17 |
| 二 | 6 | 22 |
| 三 | 3.5 | 12 |
科目:gzsx 来源: 题型:
| 月份 | 用水量(立方米) | 水费(元) |
| 一 | 4 | 17 |
| 二 | 5 | 23 |
| 三 | 2.5 | 11 |
科目:gzsx 来源: 题型:
科目:gzsx 来源:福建省厦门六中2011-2012学年高一上学期期中数学试题 题型:044
我国是水资源比较贫乏的国家之一,各地采用价格调控等手段以达到节约用水的目的.某市用水收费标准是:水费=基本费+超额费+定额损耗费,且有如下三条规定:①若每月用水量不超过最低限量m立方米时,只付基本费9元和每户每月定额损耗费a元;②若每月用水量超过m立方米时,除了付基本费和定额损耗费外,超过部分每立方米付n元的超额费;③每户每月的定额损耗费a不超过5元.
(1)求每户每月水费y(元)与月用水量x(立方米)的函数关系;
(2)该市一家庭今年第一季度每月的用水量和支付的费用如下表所示:
试分析该家庭今年一、二、三各月份的用水量是否超过最低限量,并求m,n,a的值.
科目:gzsx 来源:广东省汕头市金山中学2010届高三期中考试数学理科试题 题型:044
我国是水资源比较贫乏的国家之一,各地采用价格调控等手段以达到节约用水的目的.某市用水收费方法是:水费=基本费+超额费+损耗费.该市规定:
①若每月用水量不超过最低限量m立方米时,只付基本费9元和每户每月的定额损耗费a元;
②若每月用水量超过m立方米时,除了付基本费和损耗费外,超过部分每立方米付n元的超额费;
③每户每月的损耗费a不超过5元.
(1)求每户每月水费y(元)和用水量x(立方米)的函数关系式;
(2)该市一家庭去年第一季度的用水量和支付的费用如下表所示:

试分析一、二、三各月份的用水量是否超过最低限量,并求m、n、a的值.
科目:gzsx 来源:黑龙江省大庆铁人中学2011届高三第二次月考数学试题 题型:044
我国是水资源比较贫乏的国家之一.目前,某市就节水问题,召开了市民听证会,并对水价进行激烈讨论,会后拟定方案如下:以户为单位,按月收缴,水价按照每户每月用水量分三级管理,第一级为每月用水量不超过12吨,每吨3.5元;第二级计量范围为超过12吨不超过18吨部分,第三级计量范围为超出18吨的部分,一、二、三级水价的单价按1∶3∶5计价.
(1)请写出每月水费y(元)与用水量x(吨)之间的函数关系;
(2)某户居民当月交纳水费为63元,该户当月用水多少吨?
科目:gzsx 来源: 题型:解答题
科目:gzsx 来源: 题型:解答题
| 月份 | 用水量(立方米) | 水费(元) |
| 一 | 4 | 17 |
| 二 | 5 | 23 |
| 三 | 2.5 | 11 |
科目:gzsx 来源:不详 题型:解答题