
| 月份 | 用水量(立方米) | 水费(元) |
| 一 | 5 | 17 |
| 二 | 6 | 22 |
| 三 | 3.5 | 12 |
|
|
|


科目:高中数学 来源: 题型:
| 1 |
| xn+1 |
| 1 |
| xn |
| n-1 |
| n |
| n+1 |
| n |
查看答案和解析>>
科目:高中数学 来源: 题型:
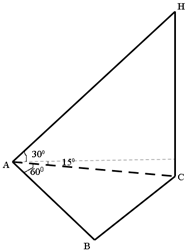 某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度:在C处进行该仪器的垂直弹射,观察点A、B两地相距100米,∠BAC=60°,其中A到C的距离比B到C的距离远40米.A地测得该仪器在C处的俯角为15°,A地测得最高点H的仰角为30°,求该仪器的垂直弹射高度CH.(结果保留根式)
某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度:在C处进行该仪器的垂直弹射,观察点A、B两地相距100米,∠BAC=60°,其中A到C的距离比B到C的距离远40米.A地测得该仪器在C处的俯角为15°,A地测得最高点H的仰角为30°,求该仪器的垂直弹射高度CH.(结果保留根式)查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| n |
| f(n)-f(m) |
| n-m |
| 1 |
| m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com