
| 产品编号 | A1 | A2 | A3 | A4 | A5 |
| 质量指标(x,y,z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
| 产品编号 | A6 | A7 | A8 | A9 | A10 |
| 质量指标(x,y,z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
| 产品编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 |
| S | 4 | 4 | 6 | 3 | 4 | 5 | 4 | 5 | 3 | 5 |
| 6 |
| 10 |
| ||||||
|
| 2 |
| 9 |
| ||||||||||||
|
| 23 |
| 45 |
| ||||||||
|
| 2 |
| 9 |
| ||||
|
| 2 |
| 45 |
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 49 |
| 45 |


科目:高中数学 来源: 题型:
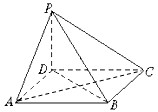 如图,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=AD.
如图,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=AD.查看答案和解析>>
科目:高中数学 来源: 题型:
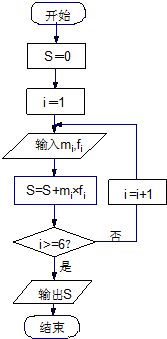 “世界睡眠日”定在每年的3月21日,2009年的世界睡眠日主题是“科学管理睡眠”,以提高公众对健康睡眠的自我管理能力和科学认识.为此某网站于2009年3月13日到3月20日持续一周网上调查公众日平均睡眠的时间(单位:小时),共有2000人参加调查,现将数据整理分组后如题中表格所示.
“世界睡眠日”定在每年的3月21日,2009年的世界睡眠日主题是“科学管理睡眠”,以提高公众对健康睡眠的自我管理能力和科学认识.为此某网站于2009年3月13日到3月20日持续一周网上调查公众日平均睡眠的时间(单位:小时),共有2000人参加调查,现将数据整理分组后如题中表格所示.| 序号(i) | 分组睡眠时间 | 组中值(mi) | 频数 (人数) | 频率(fi) |
| 1 | [4,5) | 4.5 | 80 | |
| 2 | [5,6) | 5.5 | 520 | 0.26 |
| 3 | [6,7) | 6.5 | 600 | 0.30 |
| 4 | [7,8) | 7.5 | ||
| 5 | [8,9) | 8.5 | 200 | 0.10 |
| 6 | [9,10] | 9.5 | 40 | 0.02 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,△ABC内接于⊙O,AB=AC,直线XY切⊙O于点C,BD∥XY,AC、BD相交于E.
如图所示,△ABC内接于⊙O,AB=AC,直线XY切⊙O于点C,BD∥XY,AC、BD相交于E.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在直三棱柱ABC-A1B1C1中,AC=BC=BB1=2.AB=2
如图,在直三棱柱ABC-A1B1C1中,AC=BC=BB1=2.AB=2| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com