


科目:高中数学 来源: 题型:
| 产品编号 | A1 | A2 | A3 | A4 | A5 |
| 质量指标(x,y,z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
| 产品编号 | A6 | A7 | A8 | A9 | A10 |
| 质量指标(x,y,z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x | 2 | 3 | 4 | 5 |
| Y | 18 | 27 | 32 | 35 |
 |
| y |
 |
| b |
 |
| a |
 |
| y |
 |
| b |
 |
| a |
 |
| b |
| |||||||
|
 |
| a |
. |
| y |
 |
| b |
. |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
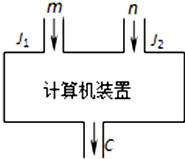 如图是一个计算机装置示意图,J1,J2是数据入口处,C是计算机结果的出口,计算过程是由J1,J2分别输入正整数m和n,经过计算后的结果由C输出.此种计算装置完成的计算满足以下三个性质:
如图是一个计算机装置示意图,J1,J2是数据入口处,C是计算机结果的出口,计算过程是由J1,J2分别输入正整数m和n,经过计算后的结果由C输出.此种计算装置完成的计算满足以下三个性质:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com