练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    解下列不等式：
    （1）-3x2+5x-4＜0
    （2）x（1-x）＞x（2x-3）+1．
    考点：一元二次不等式的解法
    专题：计算题,不等式的解法及应用
    分析：（1）把不等式整理为标准形式，由△符号及二次函数的图象可得解集；
    （2）化简不等式，求出对应方程的根，由图象可得解集；
    解答： 解：（1）-3x2+5x-4＜0可化为3x2-5x+4＞0，
    △=（-5）2-4×3×4=-23＜0，
    则函数y=3x2-5x+4的图象开口向上，与x轴无交点，
    ∴原不等式的解集为R；
    （2）x（1-x）＞x（2x-3）+1可化为3x2-4x+1＜0，即（3x-1）（x-1）＜0，
    ∴原不等式的解集为{x|
    1
    3
    ＜    x＜1}．
    点评：该题考查一元二次不等式的解法，属基础题，注意数形结合思想在解题中的运用．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

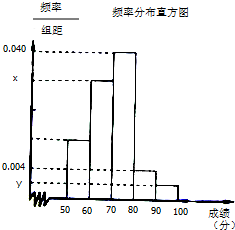    某中学举行了一次“环保知识竞赛”，全校学生参加了这次竞赛，为了了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分取正整数，满分为100分）作为样本进行统计．请根据下面尚未完成的频率分布表和频率分布直方图（如图所示）解决下列问题：
    组别分组频数频率
    第1组[50，60）80.16
    第2组[60，70）a
    第3组[70，80）200.40
    第4组[80，90）0.08
    第5组[90，100）2b
    合计
    （Ⅰ）写出a、b、x、y的值；
    （Ⅱ）在选取的样本中，从竞赛成绩是80分以上（含80分）的同学中随机抽取2名同学现广场参加环保知识的志愿宣传活动，求所抽取的2名同学中至少有1名同学来自第5组的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

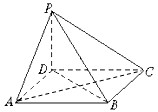    如图，四棱锥P-ABCD的底面ABCD为正方形，PD⊥底面ABCD，PD=AD．
    （1）求证：平面PAC⊥平面PBD；
    （2）求PC与平面PBD所成的角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=lnx-
    ax2
    2
    +（a-1）x-
    3
    2a
    ，其中a＞0
    （Ⅰ）求函数f（x）的单调区间；
    （Ⅱ）若函数f（x）有两个相异的零点x1，x2，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某企业要建造一个容积为18m3，深为2m的长方体形无盖贮水池，如果池底和池壁每平方米的造价分别为200元和150元，怎样设计该水池可使得能总造价最低？最低总造价为多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

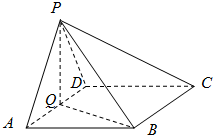    如图，在四棱锥中P-ABCD中，底面ABCD为菱形，∠BAD=60°，Q为AD的中点．
    （Ⅰ）若PA=PD，求证：平面PQB⊥平面PAD；
    （Ⅱ）若平面PAD⊥平面ABCD，且PA=PD=AD=2，点M在线段PC上，且PM=2MC，求三棱锥P-QBM的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

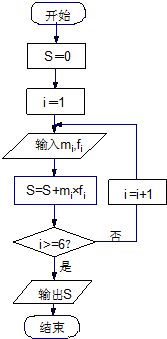    “世界睡眠日”定在每年的3月21日，2009年的世界睡眠日主题是“科学管理睡眠”，以提高公众对健康睡眠的自我管理能力和科学认识．为此某网站于2009年3月13日到3月20日持续一周网上调查公众日平均睡眠的时间（单位：小时），共有2000人参加调查，现将数据整理分组后如题中表格所示．
    （1）求出表中空白处的数据，并将表格补充完整；
    （2）画出频率分布直方图；
    （3）为了对数据举行分析，采用了计算机辅助计算．分析中一部分计算见算法流程图，求输出的S值． 
    序号（i）分组睡眠时间组中值（mi）频数
    （人数）    		频率（fi）
    1[4，5）4.580
     
    2[5，6）5.55200.26
    3[6，7）6.56000.30
    4[7，8）7.5
     
     
    5[8，9）8.52000.10
    6[9，10]9.5400.02

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图所示，△ABC内接于⊙O，AB=AC，直线XY切⊙O于点C，BD∥XY，AC、BD相交于E．
    （1）求证：△ABE≌△ACD；
    （2）若AB=6cm，BC=4cm，求AE的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    对于任意正整数n，猜想2n-1与（n+1）2的大小关系，并给出证明．

    查看答案和解析>>

    同步练习册答案