
科目:czsx 来源: 题型:
 如图,Rt△ABC中,斜边AB在x轴上,C点在y轴上,A点坐标为(-2,0),B点坐标为(8,0),
如图,Rt△ABC中,斜边AB在x轴上,C点在y轴上,A点坐标为(-2,0),B点坐标为(8,0),科目:czsx 来源: 题型:解答题
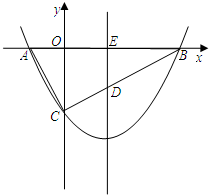 如图,Rt△ABC中,斜边AB在x轴上,C点在y轴上,A点坐标为(-2,0),B点坐标为(8,0),
如图,Rt△ABC中,斜边AB在x轴上,C点在y轴上,A点坐标为(-2,0),B点坐标为(8,0),科目:czsx 来源: 题型:解答题
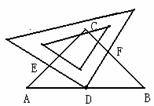
 如图,在Rt△ABC的直角边AB,斜边AC上分别找点E,F,使AE=AF.将△AFE绕点A顺时针方向旋转,EF的中点O恰好落在AB的中点,延长AF交BC于D,连接BE.
如图,在Rt△ABC的直角边AB,斜边AC上分别找点E,F,使AE=AF.将△AFE绕点A顺时针方向旋转,EF的中点O恰好落在AB的中点,延长AF交BC于D,连接BE.科目:czsx 来源: 题型:
 如图在Rt△ABC中,∠C 为直角,AC=6,BC=8.现在Rt△ABC内从左往右叠放边长为1的正方形小纸片,第一层小纸片的一条边都在AB上,依次这样往上叠放上去,则最多能叠放
如图在Rt△ABC中,∠C 为直角,AC=6,BC=8.现在Rt△ABC内从左往右叠放边长为1的正方形小纸片,第一层小纸片的一条边都在AB上,依次这样往上叠放上去,则最多能叠放科目:czsx 来源: 题型:
如图,在Rt△ABC中,∠ACB=90°,BC>AC,以斜边AB所在直线为x轴,以斜边AB上的高所在直线为y轴,建立直角坐标系,若OA2+OB2=17,且线段O( )
A.OB的长度是关于x的一元二次方程x2-mx+2(m-3)=0的两个根.
(1)求C点的坐标;
(2)以斜边AB为直径作圆与y轴交于另一点E,求过( )
A. B.E三点的抛物线的解析式,并画出此抛物线的草图;
(3)在抛物线上是否存在点P,使△ABP与△ABC全等?若存在,求出符合条件的P点的坐标;若不存在,说明理由.
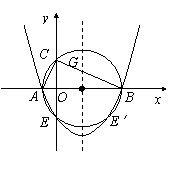
科目:czsx 来源:2012年人教版初中数学九年级下26.2用函数观点看一元二次方程练习卷(解析版) 题型:解答题
如图,在Rt△ABC中,∠ACB=90°,BC>AC,以斜边AB 所在直线为x轴,以斜边AB上的高所在直线为y轴,建立直角坐标系,若OA2+OB2= 17, 且线段OA、OB的长度是关于x的一元二次方程x2-mx+2(m-3)=0的两个根.
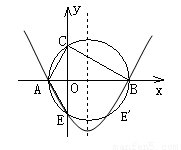
(1)求C点的坐标;
(2)以斜边AB为直径作圆与y轴交于另一点E,求过A、B、E 三点的抛物线的关系式,并画出此抛物线的草图.
(3)在抛物线上是否存在点P,使△ABP与△ABC全等?若存在,求出符合条件的P点的坐标;若不存在,说明理由.
科目:czsx 来源: 题型:填空题
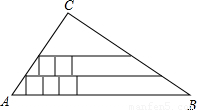
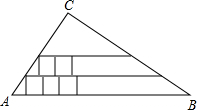 如图在Rt△ABC中,∠C 为直角,AC=6,BC=8.现在Rt△ABC内从左往右叠放边长为1的正方形小纸片,第一层小纸片的一条边都在AB上,依次这样往上叠放上去,则最多能叠放________个.
如图在Rt△ABC中,∠C 为直角,AC=6,BC=8.现在Rt△ABC内从左往右叠放边长为1的正方形小纸片,第一层小纸片的一条边都在AB上,依次这样往上叠放上去,则最多能叠放________个.科目:czsx 来源: 题型:
如图,在RtΔABC中, ∠ACB=90O,AC=BC,点D是AB的中点,将一块直角三角形板的直角顶点放在点D处旋转,两直角边分别交AC于点E,交BC于点F.则图中除了已知的相等的线段外,还有哪些线段相等?请找出来,并对其中![]() 一对说明相等的理由.
一对说明相等的理由.
科目:czsx 来源:2011-2012学年浙江省杭州市九年级(上)月考数学试卷(12月份)(解析版) 题型:填空题

科目:czsx 来源:2012年浙江省杭州市中考数学模拟试卷(49)(解析版) 题型:填空题
科目:czsx 来源:不详 题型:填空题

科目:czsx 来源: 题型:
 在Rt△ABC中,斜边AB=2BC,以直线AC为对称轴,点B的对称点是B′,如图,则与线段BC相等的线段是
在Rt△ABC中,斜边AB=2BC,以直线AC为对称轴,点B的对称点是B′,如图,则与线段BC相等的线段是科目:czsx 来源:同步题 题型:解答题
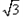 ,求线段 BD、BE 与劣弧DE所围成的图形面积. (结果保留根号和π)
,求线段 BD、BE 与劣弧DE所围成的图形面积. (结果保留根号和π)

科目:czsx 来源: 题型:
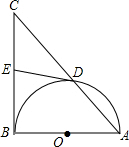 如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连接DE.
如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连接DE.科目:czsx 来源: 题型:
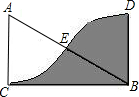 如图,在Rt△ABC中,斜边AB长为8
如图,在Rt△ABC中,斜边AB长为8| 3 |
| A、27 | B、42 | C、56 | D、108 |
科目:czsx 来源: 题型:
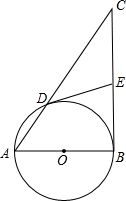 已知:以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于点D,E为BC边上的中点,连接DE.
已知:以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于点D,E为BC边上的中点,连接DE.科目:czsx 来源: 题型:
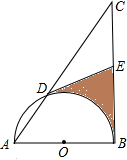 如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于点D,E是BC边的中点,连接DE.
如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于点D,E是BC边的中点,连接DE.科目:czsx 来源: 题型:
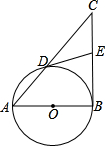 如图,以Rt△ABC的直角边AB为直径作圆O与斜边AC交于点D,E为BC边的中点,连接DE.
如图,以Rt△ABC的直角边AB为直径作圆O与斜边AC交于点D,E为BC边的中点,连接DE.科目:czsx 来源:中考备考专家数学(第二版) 题型:044
已知:以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于点D,E为BC边上的中点,连结DE.

(1)如图,求证:DE是⊙O的切线;
(2)连结OE、AE,当∠CAB为何值时,四边形AOED是平行四边形,并在此条件下求sin∠CAE的值.
(第(2)问答题要求:不要求写出解题过程,只需将结果填写在答题卡相应题号的横线上.)
科目:czsx 来源:非常讲解·教材全解全析 数学 九年级下 (配北师大课标) 配北师大课标 题型:044
已知:以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于点D,E为BC边上的中点,连结DE.
(1)如下图,求证:DE是⊙O的切线;
(2)连结OE、AE,当∠CAB为何值时,四边形AOED是平行四边形,并在此条件下求sin∠CAB的值.
