如图.数轴上线段AB=2单位长度.CD=4单位长度.点A在数轴上表示的数是答案解析
科目:czsx
来源:
题型:
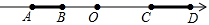
已知,如图数轴上线段AB=2(单位长度),线段CD=4(单位长度)点A在数轴上表示的是-10,点C在数轴上表示的数是16,若线段AB以每秒6个单位长度的速度向右匀速运动,同时线段CD以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒.
(1)当点B与点C相遇时,求t的值.
(2)当t为何值时,点B刚好与线段CD的中点重合?
(3)当运动到BC=8(单位长度)时,求出此时点B在数轴上表示的数.
查看答案和解析>>
科目:czsx
来源:
题型:
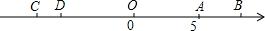
如图,数轴上有两条线段AB和CD,线段AB的长度为4个单位,线段CD的长度为2个单位,点A在数轴上表示的数是5,且A、D两点之间的距离为11.
(1)填空:点B在数轴上表示的数是
,点C在数轴上表示的数是
;
(2)若线段CD以每秒3个单位的速度向右匀速运动,当点D运动到A时,线段CD与线段AB开始有重叠部分,此时线段CD运动了
秒;
(3)在(2)的条件下,线段CD继续向右运动,问再经过
秒后,线段CD与线段AB不再有重叠部分;
(4)若线段AB、CD同时从图中位置出发,线段AB以每秒2个单位的速度向左匀速运动,线段CD仍以每秒3个单位的速度向右匀速运动,点P是线段CD的中点,问运动几秒时,点P与线段AB两端点(A或B)的距离为1个单位?
查看答案和解析>>
科目:czsx
来源:2015-2016学年河北省石家庄市栾城县七年级上学期期末数学试卷(解析版)
题型:解答题
如图,数轴上有两条线段AB和CD,线段AB的长度为4个单位,线段CD的长度为2个单位,点A在数轴上表示的数是5,且A、D两点之间的距离为11.

(1)填空:点B在数轴上表示的数是 ,点C在数轴上表示的数是 ;
(2)若线段CD以每秒3个单位的速度向右匀速运动,当点D运动到A时,线段CD与线段AB开始有重叠部分,此时线段CD运动了 秒;
(3)在(2)的条件下,线段CD继续向右运动,问再经过 秒后,线段CD与线段AB不再有重叠部分;
(4)若线段AB、CD同时从图中位置出发,线段AB以每秒2个单位的速度向左匀速运动,线段CD仍以每秒3个单位的速度向右匀速运动,点P是线段CD的中点,问运动几秒时,点P与线段AB两端点(A或B)的距离为1个单位?
查看答案和解析>>
科目:czsx
来源:
题型:
如图,在平面直角坐标系中,一底角为60°的等腰梯形ABCD的下底AB在x轴的正半轴上,A为坐标原点,点B的坐标为(m,0),对角线BD平分∠ABC,一动点P在BD上以每秒一个单位长度的速度由B→D运动(点P不与B,D重合).过P作PE⊥BD交AB于
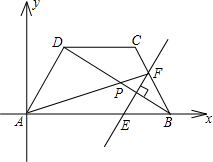
点E,交线段BC(或CD)于点F.
(1)用含m的代数式表示线段AD的长是
;
(2)当直线PE经过点C时,它的解析式为y=
x-2
,求m的值;
(3)在上述结论下,设动点P运动了t秒时,△AEF的面积为S,求S与t的函数关系式;并写出t为何值时,S取得最大值,最大值是多少?
查看答案和解析>>
科目:czsx
来源:
题型:
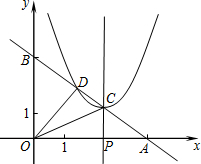
如图,直线y=-
x+3分别交x轴、y轴于A、B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,设运动时间为t秒.
(1)直接填出两点的坐标:A:
(4,0)
(4,0)
,B:
(0,3)
(0,3)
;
(2)过点P作直线截△ABO,使截得的三角形与△ABO相似,若当P在某一位置时,满足条件的直线共有4条,t的取值范围是
;
(3)如图,过点P作x轴的垂线交直线AB于点C,设以C为顶点的抛物线 y=(x+m)
2+n与直线AB的另一交点为D,
①用含t的代数式分别表示m=
-t
-t
,n=
;
②随着点P运动,CD的长是否为定值?若是,请求出CD长;若不是,说明理由;
③设△COD的OC边上的高为h,请直接写出当t为何值时,h的值最大?
查看答案和解析>>
科目:czsx
来源:
题型:
如图,数轴上线段AB=2(单位长度),CD=4(单位长度),点A在数轴上表示的数是-10,点C在数轴上表示的数是16.若线段AB以6个单位长度/秒的速度向右匀速运动,同时线段CD以2个单位长度/秒的速度向左匀速运动.

(1)问运动多少时BC=8(单位长度)?
(2)当运动到BC=8(单位长度)时,点B在数轴上表示的数是
4或40
4或40
;
(3)P是线段AB上一点,当B点运动到线段CD上时,是否存在关系式
=3,若存在,求线段PD的长;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(38):2.7 最大面积是多少(解析版)
题型:解答题
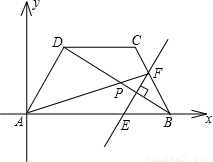
如图,在平面直角坐标系中,一底角为60°的等腰梯形ABCD的下底AB在x轴的正半轴上,A为坐标原点,点B的坐标为(m,0),对角线BD平分∠ABC,一动点P在BD上以每秒一个单位长度的速度由B→D运动(点P不与B,D重合).过P作PE⊥BD交AB于点E,交线段BC(或CD)于点F.
(1)用含m的代数式表示线段AD的长是______;
(2)当直线PE经过点C时,它的解析式为y=

x-2

,求m的值;
(3)在上述结论下,设动点P运动了t秒时,△AEF的面积为S,求S与t的函数关系式;并写出t为何值时,S取得最大值,最大值是多少?
查看答案和解析>>
科目:czsx
来源:第34章《二次函数》中考题集(42):34.4 二次函数的应用(解析版)
题型:解答题
如图,在平面直角坐标系中,一底角为60°的等腰梯形ABCD的下底AB在x轴的正半轴上,A为坐标原点,点B的坐标为(m,0),对角线BD平分∠ABC,一动点P在BD上以每秒一个单位长度的速度由B→D运动(点P不与B,D重合).过P作PE⊥BD交AB于点E,交线段BC(或CD)于点F.
(1)用含m的代数式表示线段AD的长是______;
(2)当直线PE经过点C时,它的解析式为y=

x-2

,求m的值;
(3)在上述结论下,设动点P运动了t秒时,△AEF的面积为S,求S与t的函数关系式;并写出t为何值时,S取得最大值,最大值是多少?

查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(41):2.3 二次函数的应用(解析版)
题型:解答题
如图,在平面直角坐标系中,一底角为60°的等腰梯形ABCD的下底AB在x轴的正半轴上,A为坐标原点,点B的坐标为(m,0),对角线BD平分∠ABC,一动点P在BD上以每秒一个单位长度的速度由B→D运动(点P不与B,D重合).过P作PE⊥BD交AB于点E,交线段BC(或CD)于点F.
(1)用含m的代数式表示线段AD的长是______;
(2)当直线PE经过点C时,它的解析式为y=

x-2

,求m的值;
(3)在上述结论下,设动点P运动了t秒时,△AEF的面积为S,求S与t的函数关系式;并写出t为何值时,S取得最大值,最大值是多少?

查看答案和解析>>
科目:czsx
来源:第6章《二次函数》中考题集(41):6.4 二次函数的应用(解析版)
题型:解答题
如图,在平面直角坐标系中,一底角为60°的等腰梯形ABCD的下底AB在x轴的正半轴上,A为坐标原点,点B的坐标为(m,0),对角线BD平分∠ABC,一动点P在BD上以每秒一个单位长度的速度由B→D运动(点P不与B,D重合).过P作PE⊥BD交AB于点E,交线段BC(或CD)于点F.
(1)用含m的代数式表示线段AD的长是______;
(2)当直线PE经过点C时,它的解析式为y=

x-2

,求m的值;
(3)在上述结论下,设动点P运动了t秒时,△AEF的面积为S,求S与t的函数关系式;并写出t为何值时,S取得最大值,最大值是多少?

查看答案和解析>>
科目:czsx
来源:第27章《二次函数》中考题集(40):27.3 实践与探索(解析版)
题型:解答题
如图,在平面直角坐标系中,一底角为60°的等腰梯形ABCD的下底AB在x轴的正半轴上,A为坐标原点,点B的坐标为(m,0),对角线BD平分∠ABC,一动点P在BD上以每秒一个单位长度的速度由B→D运动(点P不与B,D重合).过P作PE⊥BD交AB于点E,交线段BC(或CD)于点F.
(1)用含m的代数式表示线段AD的长是______;
(2)当直线PE经过点C时,它的解析式为y=

x-2

,求m的值;
(3)在上述结论下,设动点P运动了t秒时,△AEF的面积为S,求S与t的函数关系式;并写出t为何值时,S取得最大值,最大值是多少?

查看答案和解析>>
科目:czsx
来源:第26章《二次函数》中考题集(39):26.3 实际问题与二次函数(解析版)
题型:解答题
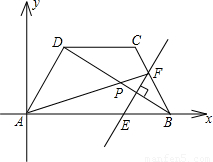
如图,在平面直角坐标系中,一底角为60°的等腰梯形ABCD的下底AB在x轴的正半轴上,A为坐标原点,点B的坐标为(m,0),对角线BD平分∠ABC,一动点P在BD上以每秒一个单位长度的速度由B→D运动(点P不与B,D重合).过P作PE⊥BD交AB于点E,交线段BC(或CD)于点F.
(1)用含m的代数式表示线段AD的长是______;
(2)当直线PE经过点C时,它的解析式为y=

x-2

,求m的值;
(3)在上述结论下,设动点P运动了t秒时,△AEF的面积为S,求S与t的函数关系式;并写出t为何值时,S取得最大值,最大值是多少?
查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(42):2.8 二次函数的应用(解析版)
题型:解答题
如图,在平面直角坐标系中,一底角为60°的等腰梯形ABCD的下底AB在x轴的正半轴上,A为坐标原点,点B的坐标为(m,0),对角线BD平分∠ABC,一动点P在BD上以每秒一个单位长度的速度由B→D运动(点P不与B,D重合).过P作PE⊥BD交AB于点E,交线段BC(或CD)于点F.
(1)用含m的代数式表示线段AD的长是______;
(2)当直线PE经过点C时,它的解析式为y=

x-2

,求m的值;
(3)在上述结论下,设动点P运动了t秒时,△AEF的面积为S,求S与t的函数关系式;并写出t为何值时,S取得最大值,最大值是多少?

查看答案和解析>>
科目:czsx
来源:第20章《二次函数和反比例函数》中考题集(38):20.5 二次函数的一些应用(解析版)
题型:解答题
如图,在平面直角坐标系中,一底角为60°的等腰梯形ABCD的下底AB在x轴的正半轴上,A为坐标原点,点B的坐标为(m,0),对角线BD平分∠ABC,一动点P在BD上以每秒一个单位长度的速度由B→D运动(点P不与B,D重合).过P作PE⊥BD交AB于点E,交线段BC(或CD)于点F.
(1)用含m的代数式表示线段AD的长是______;
(2)当直线PE经过点C时,它的解析式为y=

x-2

,求m的值;
(3)在上述结论下,设动点P运动了t秒时,△AEF的面积为S,求S与t的函数关系式;并写出t为何值时,S取得最大值,最大值是多少?

查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(39):2.4 二次函数的应用(解析版)
题型:解答题
如图,在平面直角坐标系中,一底角为60°的等腰梯形ABCD的下底AB在x轴的正半轴上,A为坐标原点,点B的坐标为(m,0),对角线BD平分∠ABC,一动点P在BD上以每秒一个单位长度的速度由B→D运动(点P不与B,D重合).过P作PE⊥BD交AB于点E,交线段BC(或CD)于点F.
(1)用含m的代数式表示线段AD的长是______;
(2)当直线PE经过点C时,它的解析式为y=
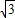
x-2

,求m的值;
(3)在上述结论下,设动点P运动了t秒时,△AEF的面积为S,求S与t的函数关系式;并写出t为何值时,S取得最大值,最大值是多少?

查看答案和解析>>
科目:czsx
来源:第23章《二次函数与反比例函数》中考题集(38):23.5 二次函数的应用(解析版)
题型:解答题
如图,在平面直角坐标系中,一底角为60°的等腰梯形ABCD的下底AB在x轴的正半轴上,A为坐标原点,点B的坐标为(m,0),对角线BD平分∠ABC,一动点P在BD上以每秒一个单位长度的速度由B→D运动(点P不与B,D重合).过P作PE⊥BD交AB于点E,交线段BC(或CD)于点F.
(1)用含m的代数式表示线段AD的长是______;
(2)当直线PE经过点C时,它的解析式为y=

x-2

,求m的值;
(3)在上述结论下,设动点P运动了t秒时,△AEF的面积为S,求S与t的函数关系式;并写出t为何值时,S取得最大值,最大值是多少?

查看答案和解析>>
科目:czsx
来源:2012年江苏省南京市金陵中学河西分校中考数学一模试卷(解析版)
题型:解答题
如图,直线y=-

x+3分别交x轴、y轴于A、B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,设运动时间为t秒.
(1)直接填出两点的坐标:A:______,B:______;
(2)过点P作直线截△ABO,使截得的三角形与△ABO相似,若当P在某一位置时,满足条件的直线共有4条,t的取值范围是______;
(3)如图,过点P作x轴的垂线交直线AB于点C,设以C为顶点的抛物线 y=(x+m)
2+n与直线AB的另一交点为D,
①用含t的代数式分别表示m=______,n=______;
②随着点P运动,CD的长是否为定值?若是,请求出CD长;若不是,说明理由;
③设△COD的OC边上的高为h,请直接写出当t为何值时,h的值最大?

查看答案和解析>>
科目:czsx
来源:2009年河南省商丘市睢县高级中学高一新生入学考试数学试卷(解析版)
题型:解答题
如图,在平面直角坐标系中,一底角为60°的等腰梯形ABCD的下底AB在x轴的正半轴上,A为坐标原点,点B的坐标为(m,0),对角线BD平分∠ABC,一动点P在BD上以每秒一个单位长度的速度由B→D运动(点P不与B,D重合).过P作PE⊥BD交AB于点E,交线段BC(或CD)于点F.
(1)用含m的代数式表示线段AD的长是______;
(2)当直线PE经过点C时,它的解析式为y=

x-2

,求m的值;
(3)在上述结论下,设动点P运动了t秒时,△AEF的面积为S,求S与t的函数关系式;并写出t为何值时,S取得最大值,最大值是多少?

查看答案和解析>>
科目:czsx
来源:2008年北京市通州区中考数学二模试卷(解析版)
题型:解答题
如图,在平面直角坐标系中,一底角为60°的等腰梯形ABCD的下底AB在x轴的正半轴上,A为坐标原点,点B的坐标为(m,0),对角线BD平分∠ABC,一动点P在BD上以每秒一个单位长度的速度由B→D运动(点P不与B,D重合).过P作PE⊥BD交AB于点E,交线段BC(或CD)于点F.
(1)用含m的代数式表示线段AD的长是______;
(2)当直线PE经过点C时,它的解析式为y=
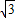
x-2

,求m的值;
(3)在上述结论下,设动点P运动了t秒时,△AEF的面积为S,求S与t的函数关系式;并写出t为何值时,S取得最大值,最大值是多少?

查看答案和解析>>
科目:czsx
来源:2010年吉林省长春市中考数学三模试卷(解析版)
题型:解答题
如图,在平面直角坐标系中,一底角为60°的等腰梯形ABCD的下底AB在x轴的正半轴上,A为坐标原点,点B的坐标为(m,0),对角线BD平分∠ABC,一动点P在BD上以每秒一个单位长度的速度由B→D运动(点P不与B,D重合).过P作PE⊥BD交AB于点E,交线段BC(或CD)于点F.
(1)用含m的代数式表示线段AD的长是______;
(2)当直线PE经过点C时,它的解析式为y=

x-2
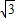
,求m的值;
(3)在上述结论下,设动点P运动了t秒时,△AEF的面积为S,求S与t的函数关系式;并写出t为何值时,S取得最大值,最大值是多少?

查看答案和解析>>

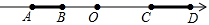 已知,如图数轴上线段AB=2(单位长度),线段CD=4(单位长度)点A在数轴上表示的是-10,点C在数轴上表示的数是16,若线段AB以每秒6个单位长度的速度向右匀速运动,同时线段CD以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒.
已知,如图数轴上线段AB=2(单位长度),线段CD=4(单位长度)点A在数轴上表示的是-10,点C在数轴上表示的数是16,若线段AB以每秒6个单位长度的速度向右匀速运动,同时线段CD以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒.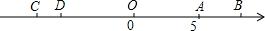 如图,数轴上有两条线段AB和CD,线段AB的长度为4个单位,线段CD的长度为2个单位,点A在数轴上表示的数是5,且A、D两点之间的距离为11.
如图,数轴上有两条线段AB和CD,线段AB的长度为4个单位,线段CD的长度为2个单位,点A在数轴上表示的数是5,且A、D两点之间的距离为11.
 点E,交线段BC(或CD)于点F.
点E,交线段BC(或CD)于点F. 如图,直线y=-
如图,直线y=-
 x-2
x-2 ,求m的值;
,求m的值;
 x-2
x-2 ,求m的值;
,求m的值;
 x-2
x-2 ,求m的值;
,求m的值;
 x-2
x-2 ,求m的值;
,求m的值;
 x-2
x-2 ,求m的值;
,求m的值;
 x-2
x-2 ,求m的值;
,求m的值;
 x-2
x-2 ,求m的值;
,求m的值;
 x-2
x-2 ,求m的值;
,求m的值;
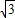 x-2
x-2 ,求m的值;
,求m的值;
 x-2
x-2 ,求m的值;
,求m的值;
 x+3分别交x轴、y轴于A、B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,设运动时间为t秒.
x+3分别交x轴、y轴于A、B两点,线段OA上有一动点P由原点O向点A运动,速度为每秒1个单位长度,设运动时间为t秒.
 x-2
x-2 ,求m的值;
,求m的值;
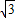 x-2
x-2 ,求m的值;
,求m的值;
 x-2
x-2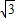 ,求m的值;
,求m的值;