精英家教网 >
试题搜索列表 >如图.在平面直角坐标系中.二次函数y=x2+bx+c的图象与x轴交于A.B两点
如图.在平面直角坐标系中.二次函数y=x2+bx+c的图象与x轴交于A.B两点答案解析
科目:czsx
来源:2003年上海市中考数学试题
题型:059
|
|
已知在平面直角坐标系内,O为坐标原点,A、B是x轴正半轴上的两点,点A在点B的左侧,如图,二次函数y=a x2+bx+c(a≠0)的图象经过点A、B,与y轴相交于点C.

| (1) |
|
(2) |
|
如果线段OC的长度是线段OA、OB长度的比例中项,试证a、c互为倒数;
|
|
(3) |
|
在(2)的条件下,如果b=-4,AB= ,求a、c的值. ,求a、c的值.
|
|
|
查看答案和解析>>
科目:czsx
来源:
题型:解答题
13.
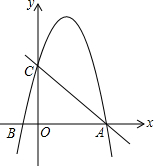
如图,平面直角坐标系xOy中,已知B(-1,0),一次函数y=-x+5的图象与x轴、y轴分别交于点A、C两点,二次函数y=-x
2+bx+c的图象经过点A、点B.
(1)求这个二次函数的解析式;
(2)点P是该二次函数图象的顶点,求△APC的面积;
(3)如果点Q在线段AC上,且△ABC与△AOQ相似,求点Q的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
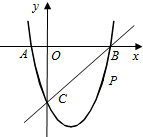
如图,在平面直角坐标系中,二次函数y=x
2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的表达式.
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
查看答案和解析>>
科目:czsx
来源:
题型:
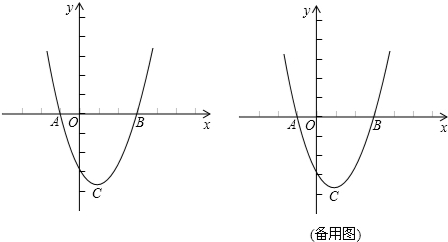
如图,在平面直角坐标系xOy中,二次函数
y=x2+bx+c的图象与x轴交于A(-1,0)、B(3,0)两点,顶点为C.
(1)求此二次函数解析式;
(2)点D为点C关于x轴的对称点,过点A作直线l:
y=x+交BD于点E,过点B作直线BK∥AD交直线l于K点.问:在四边形ABKD的内部是否存在点P,使得它到四边形ABKD四边的距离都相等?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)在(2)的条件下,若M、N分别为直线AD和直线l上的两个动点,连结DN、NM、MK,求DN+NM+MK和的最小值.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在平面直角坐标系中,二次函数y=x
2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
(1)分别求出图中直线和抛物线的函数表达式;
(2)连接PO、PC,并把△POC沿C O翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,在平面直角坐标系中,二次函数y=x
2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的

坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的表达式.
(2)当点P运动到什么位置时,四边形ABPC为等腰梯形,直接写出此时P点的坐标:P(
2
2
,
-3
-3
).
(3)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在平面直角坐标系xOy中,二次函数
y=-x2+bx-2的图象与y轴交于C点,与x轴交于A、B两点(A点在B点右侧),一次函数y=mx+n(m≠0)的图象经过A、C两点,已知
tan∠BAC=.
(1)求该二次函数和一次函数的解析式;
(2)连接BC,求△ABC的面积.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在平面直角坐标系中,二次函数y=x
2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的解析式;
(2)当点P运动到什么位置时,四边形ABPC的面积最大,并求出此时P点的坐标和四边形ABPC的最大面积.
查看答案和解析>>
科目:czsx
来源:福建省厦门外国语学校2011届九年级上学期期中考试数学试题
题型:044
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方 的抛物线上一动点.
的抛物线上一动点.

(1)求b,c的值
.
(2)连结PO、PC,并把△POC沿CO翻折,得到四边形PO C,那么是否存在点P,使四边形PO
C,那么是否存在点P,使四边形PO C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形ABPC的面积最大,并求出此时P点的坐标和四边形ABPC的最大面积.
查看答案和解析>>
科目:czsx
来源:2013年山东省枣庄市高级中等学校招生考试数学
题型:044
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.

(1)求二次函数解析式;
(2)连接PO,PC,并将△POC沿y轴对折,得到四边形PO C.是否存在点P,使四边形PO
C.是否存在点P,使四边形PO C为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
C为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
查看答案和解析>>
科目:czsx
来源:2010年湖北省恩施自治州初中毕业及高中招生考试数学试题
题型:044
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.

(1)求这个二次函数的表达式
.
(2)连结PO、PC,并把△POC沿CO翻折,得到四边形PO C,那么是否存在点P,使四边形PO
C,那么是否存在点P,使四边形PO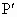 C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形ABPC的面积最大并求出此时P点的坐标和四边形ABPC的最大面积.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的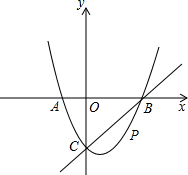 坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的表达式.
(2)当点P运动到什么位置时,四边形ABPC为等腰梯形,直接写出此时P点的坐标:P(______,______).
(3)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
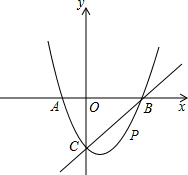 如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
(1)分别求出图中直线和抛物线的函数表达式;
(2)连接PO、PC,并把△POC沿C O翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
 如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的解析式;
(2)当点P运动到什么位置时,四边形ABPC的面积最大,并求出此时P点的坐标和四边形ABPC的最大面积.
查看答案和解析>>
科目:czsx
来源:湖北省中考真题
题型:解答题
如图所示,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点。
(1)求这个二次函数的表达式;
(2)连结PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由;
(3)当点P运动到什么位置时,四边形ABPC的面积最大并求出此时P点的坐标和四边形ABPC的最大面积。
查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(31):2.3 二次函数的应用(解析版)
题型:解答题

如图,在平面直角坐标系中,二次函数y=x
2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的表达式.
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
查看答案和解析>>
科目:czsx
来源:第6章《二次函数》中考题集(31):6.4 二次函数的应用(解析版)
题型:解答题

如图,在平面直角坐标系中,二次函数y=x
2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的表达式.
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
查看答案和解析>>
科目:czsx
来源:2010-2011学年浙江省湖州市吴兴区九年级(上)期末数学试卷(解析版)
题型:解答题
如图,在平面直角坐标系中,二次函数y=x
2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的解析式;
(2)当点P运动到什么位置时,四边形ABPC的面积最大,并求出此时P点的坐标和四边形ABPC的最大面积.

查看答案和解析>>
科目:czsx
来源:2011-2012学年四川省成都市高新区九年级(上)期末数学试卷(解析版)
题型:解答题
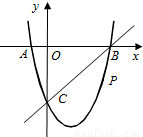
如图,在平面直角坐标系中,二次函数y=x
2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的表达式.
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
查看答案和解析>>
科目:czsx
来源:2011-2012学年河南省郑州市新密市九年级(上)期末数学试卷(解析版)
题型:解答题

如图,在平面直角坐标系中,二次函数y=x
2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
(1)求这个二次函数的表达式.
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
查看答案和解析>>

 如图,平面直角坐标系xOy中,已知B(-1,0),一次函数y=-x+5的图象与x轴、y轴分别交于点A、C两点,二次函数y=-x2+bx+c的图象经过点A、点B.
如图,平面直角坐标系xOy中,已知B(-1,0),一次函数y=-x+5的图象与x轴、y轴分别交于点A、C两点,二次函数y=-x2+bx+c的图象经过点A、点B. 如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
 如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点. 坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点. 如图,在平面直角坐标系xOy中,二次函数y=-
如图,在平面直角坐标系xOy中,二次函数y=- 如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.![]() 的抛物线上一动点.
的抛物线上一动点.
![]() C,那么是否存在点P,使四边形PO
C,那么是否存在点P,使四边形PO![]() C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
![]() C.是否存在点P,使四边形PO
C.是否存在点P,使四边形PO![]() C为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
C为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
![]() C,那么是否存在点P,使四边形PO
C,那么是否存在点P,使四边形PO![]() C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由. 坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点. 如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点. 如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.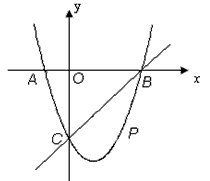
 如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点. 如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
 如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点. 如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,-3)点,点P是直线BC下方的抛物线上一动点.