
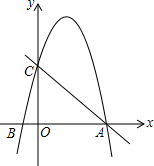
 如图,平面直角坐标系xOy中,已知B(-1,0),一次函数y=-x+5的图象与x轴、y轴分别交于点A、C两点,二次函数y=-x2+bx+c的图象经过点A、点B.
如图,平面直角坐标系xOy中,已知B(-1,0),一次函数y=-x+5的图象与x轴、y轴分别交于点A、C两点,二次函数y=-x2+bx+c的图象经过点A、点B.分析 (1)由一次函数的解析式求出A、C两点坐标,再根据A、B两点坐标求出b、c即可确定二次函数解析式;
(2)根据二次函数的解析式求出P点坐标,然后计算三角形APC的面积;
(3)分两种情况讨论:①△ABC∽△AOQ,②△ABC∽△AQO.
解答 解:(1)∵一次函数y=-x+5的图象与x轴、y轴分别交于点A、C两点,
∴A(5,0),C(0,5),
∵二次函数y=-x2+bx+c的图象经过点A、点B,
∴b=4,c=5,
∴二次函数的解析式为:y=-x2+4x+5.
(2)∵y=-x2+4x+5=-(x-2)2+9,
∴P(2,9),
过点P作PD∥y轴交AC于点D,如图,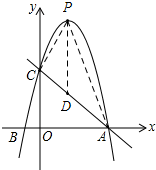
则D(2,3),
∴${S}_{△APC}=\frac{1}{2}({x}_{A}-{x}_{C})({y}_{P}-{y}_{D})$=15;
(3)①若△ABC∽△AOQ,如图,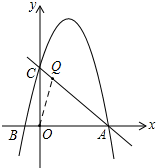
此时,OQ∥BC,
由B、C两点坐标可求得BC的解析式为:y=5x+5,
∴OQ的解析式为:y=5x,
由$\left\{\begin{array}{l}{y=5x}\\{y=-x+5}\end{array}\right.$解得:$\left\{\begin{array}{l}{x=\frac{5}{6}}\\{y=\frac{25}{6}}\end{array}\right.$,
∴Q($\frac{5}{6}$,$\frac{25}{6}$);
②若△ABC∽△AQO,如图,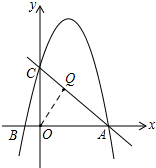
此时,$\frac{AQ}{AB}=\frac{AO}{AC}$,
∵AB=6,AO=5,AC=$5\sqrt{2}$,
∴AQ=3$\sqrt{2}$,
∴Q(2,3).
综上所述,满足要求的Q点坐标为:Q($\frac{5}{6}$,$\frac{25}{6}$)或Q(2,3).
点评 本题是二次函数综合题,主要考查了一次函数与坐标轴的交点坐标、待定系数法求二次函数解析式,铅垂高法求三角形面积、相似三角形的判定与性质,难度中等.分类讨论思想的应用是解答(3)问的关键.


 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:选择题
| A. | 3a2b+2ab2=5a3b3 | B. | 2-$\frac{2}{x-1}$=$\frac{2x-4}{x-1}$ | C. | (x-2)(-x+2)=x2-4 | D. | a2•a3+a6=2a6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
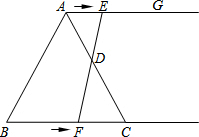 如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为ts.
如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为ts.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
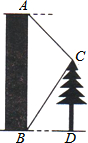 如图,某建筑物AB的高为6米,在建筑物顶端A测得一棵树CD的点C的俯角为45°,在地面点B测得点C的仰角为60°,求树高CD(结果精确到0.1米).(参考数据:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4)
如图,某建筑物AB的高为6米,在建筑物顶端A测得一棵树CD的点C的俯角为45°,在地面点B测得点C的仰角为60°,求树高CD(结果精确到0.1米).(参考数据:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,⊙O是Rt△ABC的内切圆,∠C=90°,BO的延长线交AC于点D,若BC=4,CD=2,则⊙O的半径的值是$\frac{4}{3}$.
如图,⊙O是Rt△ABC的内切圆,∠C=90°,BO的延长线交AC于点D,若BC=4,CD=2,则⊙O的半径的值是$\frac{4}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com