
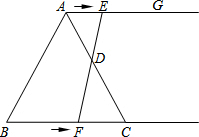
 如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为ts.
如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为ts.分析 (1)由D为AC的中点得出AC=CD,由AG∥BC可得出∠EAD=∠FCD,∠AED=∠CFD,满足全等三角形的判定定理(AAS),从而得证;
(2)①设x秒时,AE=CF,结合图形列出关于x的一元一次方程,解方程求出x的值,算出此时四边形ACFE各边的长度,得知四边形ACFE为菱形;
②由AG∥BC得知△ACE与△FCE为等高的三角形,结合三角形的面积公式设满足AE=2CF的时间为y,由路程=速度×时间列出关于y的一元一次方程,解方程即可得出结论.
解答 (1)证明:∵D为AC的中点,
∴AC=CD,
∵AG∥BC,
∴∠EAD=∠FCD,∠AED=∠CFD.
在△ADE和△CDF中,$\left\{\begin{array}{l}{∠EAD=∠FCD}\\{∠AED=∠CFD}\\{AD=CD}\end{array}\right.$,
∴△ADE≌△CDF(AAS).
(2)解:① 设x秒时,AE=CF,
设x秒时,AE=CF,
则有2x-6=x,解得x=6.
此时AE=CF=AC=6,
即四边形ACFE是菱形,
②∵AG∥BC,
∴△ACE与△FCE为等高的三角形,
当AE=2CF时,S△ACE=2S△FCE.
设满足AE=2CF的时间为y,
则有x=2|6-2x|,
解得:x=$\frac{12}{5}$,或x=4.
故答案为:①6;②$\frac{12}{5}$或4.
点评 本题考查了全等三角形的判定、等边三角形的性质以及菱形的判断,解题的关键:(1)找出符合AAS的各条件;(2)列出方程.本题属于基础题,难度不大,(1)没有难度;(2)①也好解决;②有的同学会落下一种情况,故在此处找出的是含绝对值的方程.


科目:初中数学 来源: 题型:解答题
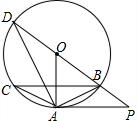 如图,⊙O是△ABC的外接圆,AB=AC,BD是⊙O的直径.PA∥BC,与DB的延长线交于点P.连结AD.
如图,⊙O是△ABC的外接圆,AB=AC,BD是⊙O的直径.PA∥BC,与DB的延长线交于点P.连结AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
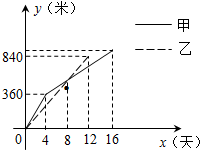 某县在实施“村村通”工程中,决定在A、B两村之间修一条公路,甲、乙两个工程队分别从A、B两村同时开始相向修路,施工期间,甲队改变了一次修路速度,乙队因另有任务提前离开,余下的任务由甲队单独完成,直到公路修通,甲、乙两个工程队各自所修公路的长度y(米)与修路时间x(天)之间的函数图象如图所示.
某县在实施“村村通”工程中,决定在A、B两村之间修一条公路,甲、乙两个工程队分别从A、B两村同时开始相向修路,施工期间,甲队改变了一次修路速度,乙队因另有任务提前离开,余下的任务由甲队单独完成,直到公路修通,甲、乙两个工程队各自所修公路的长度y(米)与修路时间x(天)之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
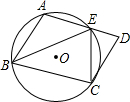 如图,A,B,C是⊙O上一点,四边形ABCD是平行四边形,CD与⊙O相切,AD与⊙O交于点E,∠D=70°,则∠BEC=( )
如图,A,B,C是⊙O上一点,四边形ABCD是平行四边形,CD与⊙O相切,AD与⊙O交于点E,∠D=70°,则∠BEC=( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
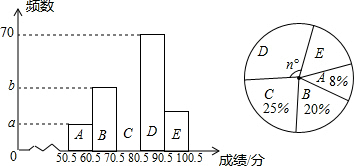
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
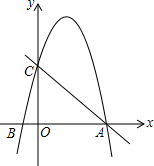 如图,平面直角坐标系xOy中,已知B(-1,0),一次函数y=-x+5的图象与x轴、y轴分别交于点A、C两点,二次函数y=-x2+bx+c的图象经过点A、点B.
如图,平面直角坐标系xOy中,已知B(-1,0),一次函数y=-x+5的图象与x轴、y轴分别交于点A、C两点,二次函数y=-x2+bx+c的图象经过点A、点B.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
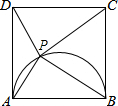 如图,已知四边形ABCD是边长为4的正方形,以AB为直径向正方形内作半圆,P为半圆上一动点(不与A、B重合),当PA=2$\sqrt{2}$或$\frac{8\sqrt{5}}{5}$时,△PAD为等腰三角形.
如图,已知四边形ABCD是边长为4的正方形,以AB为直径向正方形内作半圆,P为半圆上一动点(不与A、B重合),当PA=2$\sqrt{2}$或$\frac{8\sqrt{5}}{5}$时,△PAD为等腰三角形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>b | B. | a=b | C. | a<b | D. | 以上都有可能 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com