
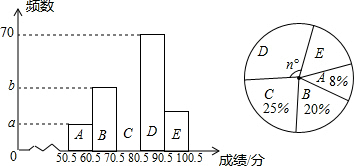
分析 (1)根据若A组的频数比B组小24,且已知两个组的百分比,据此即可求得总人数,然后根据百分比的意义求得a、b的值;
(2)利用360°乘以对应的比例即可求解;
(3)利用总人数乘以对应的百分比即可求解.
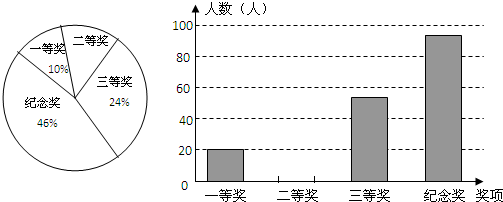
解答 解:(1)学生总数是24÷(20%-8%)=200(人),则a=200×8%=16,b=200×20%=40;
(2)n=360×$\frac{70}{200}$=126°.
C组的人数是:200×25%=50.补全频数分布直方图如下: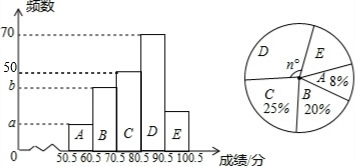
(3)2000×(1-25%-20%-8%)=940(名).
答:估计成绩优秀的学生有940名.
故答案为:(1)16,40;(2)126.
点评 本题考查的是频数分布直方图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.直方图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.也考查了利用样本估计总体的思想.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:填空题
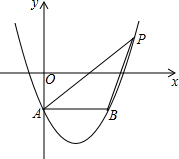 如图,在平面直角坐标系中,抛物线y=x2-2x-1交y轴于点A,过点A作AB∥x轴交抛物线于点B,点P在抛物线上,连结PA、PB,若点P关于x轴的对称点恰好落在直线AB上,则△ABP的面积是2.
如图,在平面直角坐标系中,抛物线y=x2-2x-1交y轴于点A,过点A作AB∥x轴交抛物线于点B,点P在抛物线上,连结PA、PB,若点P关于x轴的对称点恰好落在直线AB上,则△ABP的面积是2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
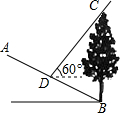 如图,斜坡AB的坡度i=1:2,坡脚B处有一棵树BC,某一时刻测得树BC在斜坡AB上的影子BD的长度为10米,这时测得太阳光线与水平线的夹角为60°,则树BC的高度为2$\sqrt{5}$+4$\sqrt{15}$米.
如图,斜坡AB的坡度i=1:2,坡脚B处有一棵树BC,某一时刻测得树BC在斜坡AB上的影子BD的长度为10米,这时测得太阳光线与水平线的夹角为60°,则树BC的高度为2$\sqrt{5}$+4$\sqrt{15}$米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
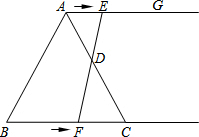 如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为ts.
如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为ts.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com