
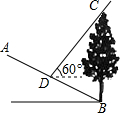
 如图,斜坡AB的坡度i=1:2,坡脚B处有一棵树BC,某一时刻测得树BC在斜坡AB上的影子BD的长度为10米,这时测得太阳光线与水平线的夹角为60°,则树BC的高度为2$\sqrt{5}$+4$\sqrt{15}$米.
如图,斜坡AB的坡度i=1:2,坡脚B处有一棵树BC,某一时刻测得树BC在斜坡AB上的影子BD的长度为10米,这时测得太阳光线与水平线的夹角为60°,则树BC的高度为2$\sqrt{5}$+4$\sqrt{15}$米. 分析 根据题意首先利用勾股定理得出DF,DE的长,再利用锐角三角函数关系得出EC的长,进而得出答案.
解答 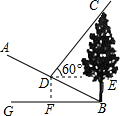 解:过点D作DF⊥BG,垂足为F,
解:过点D作DF⊥BG,垂足为F,
∵斜坡AB的坡度i=1:2,
∴设DF=x,BF=2x,则DB=10m,
∴x2+(2x)2=102,
解得:x=2$\sqrt{5}$,
故DE=4$\sqrt{5}$,BE=DF=2$\sqrt{5}$,
∵测得太阳光线与水平线的夹角为60°,
∴tan60°=$\frac{EC}{DE}$=$\frac{EC}{4\sqrt{5}}$=$\sqrt{3}$,
解得:EC=4$\sqrt{15}$,
故BC=EC+BE=2$\sqrt{5}$+4$\sqrt{15}$(m),
故答案为:2$\sqrt{5}$+4$\sqrt{15}$.
点评 此题主要考查了解直角三角形的应用以及勾股定理,正确得出DF的长是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
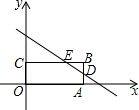 如图,在平面直角坐标系中,矩形OABC的边OA、OC分别在x轴、y轴的正半轴上,点B在第一象限,直线y=$-\frac{2}{3}x+2$与边AB、BC分别交于点D、E,若点B的坐标为(m,1),则m的值可能是( )
如图,在平面直角坐标系中,矩形OABC的边OA、OC分别在x轴、y轴的正半轴上,点B在第一象限,直线y=$-\frac{2}{3}x+2$与边AB、BC分别交于点D、E,若点B的坐标为(m,1),则m的值可能是( )| A. | -1 | B. | 1 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
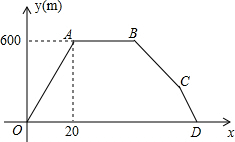 某山山脚的M处到山顶的N处有一条长为600米的登山路,小李沿此路从M走到N,停留后再原路返回,期间小李离开M处的路程y米与离开M处的时间x分(x>0)之间的函数关系如图中折线OABCD所示.
某山山脚的M处到山顶的N处有一条长为600米的登山路,小李沿此路从M走到N,停留后再原路返回,期间小李离开M处的路程y米与离开M处的时间x分(x>0)之间的函数关系如图中折线OABCD所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
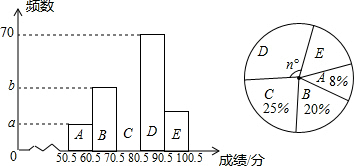
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
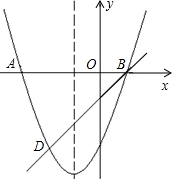 如图,二次函数y=x2+bx+c的图象与x轴交于A、B两点,且A点坐标为(-3,0),经过B点的直线交抛物线于点D(-2,-3).
如图,二次函数y=x2+bx+c的图象与x轴交于A、B两点,且A点坐标为(-3,0),经过B点的直线交抛物线于点D(-2,-3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
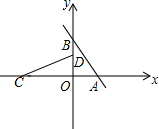 如图,直线y=-2x+4与x轴、y轴分别交于A、B两点,把△AOB绕着点O逆时针旋转90°得到△COD.
如图,直线y=-2x+4与x轴、y轴分别交于A、B两点,把△AOB绕着点O逆时针旋转90°得到△COD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 得分/分 | 0 | 1 | 2 | 3 | 4 |
| 百分率 | 15% | 10% | 25% | 40% | 10% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com