
分析 由a,b,c分别是直角三角形的三边长(假设c是斜边),根据勾股定理得出a2+b2=c2,
(1)举反例不能得出(a2)2+(b2)2=(c2)2,由勾股定理的逆定理即可判断长为a2,b2,c2的三条线段不能组成直角三角形;
(2)由a2+b2=c2,根据等式的性质以及幂的乘方的性质可得(2a)2+(2b)2=(2c)2,由勾股定理的逆定理即可判断长为2a,2b,2c的三条线段能组成直角三角形.
解答 解:∵a,b,c分别是直角三角形的三边长(假设c是斜边),
∴a2+b2=c2,
(1)不能.理由如下:
令a=3,b=4,c=5,满足a2+b2=c2,
但是(a2)2+(b2)2=81+256=337,(c2)2=625,
∴(a2)2+(b2)2≠(c2)2,
∴长为a2,b2,c2的三条线段不能组成直角三角形;
(2)能.理由如下:
∵a2+b2=c2,
∴4a2+4b2=4c2,
即(2a)2+(2b)2=(2c)2,
∴长为2a,2b,2c的三条线段能组成直角三角形.
点评 本题考查了勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.也考查了勾股定理.


科目:初中数学 来源: 题型:解答题
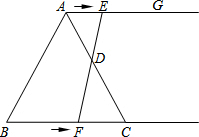 如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为ts.
如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为ts.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
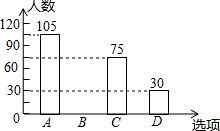 某校决定在6月8日“世界海洋日”开展系列海洋知识的宣传活动,活动有A.唱歌、B.舞蹈、C.绘画、D.演讲四项宣传方式.学校围绕“你最喜欢的宣传方式是什么?”在全校学生中进行随机抽样调查(四个选项中必选且只选一项),根据调查统计结果,绘制了如下两种不完整的统计图表:
某校决定在6月8日“世界海洋日”开展系列海洋知识的宣传活动,活动有A.唱歌、B.舞蹈、C.绘画、D.演讲四项宣传方式.学校围绕“你最喜欢的宣传方式是什么?”在全校学生中进行随机抽样调查(四个选项中必选且只选一项),根据调查统计结果,绘制了如下两种不完整的统计图表:| 选项 | 方式 | 百分比 |
| A | 唱歌 | 35% |
| B | 舞蹈 | a |
| C | 绘画 | 25% |
| D | 演讲 | 10% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
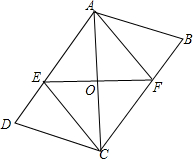 如图.四边形ABCD中,AB=CD,AD=BC,对角线AC的中点为O,过点O的直线分别交AD、BC于点E、F.
如图.四边形ABCD中,AB=CD,AD=BC,对角线AC的中点为O,过点O的直线分别交AD、BC于点E、F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com