
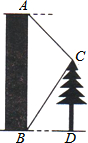
 如图,某建筑物AB的高为6米,在建筑物顶端A测得一棵树CD的点C的俯角为45°,在地面点B测得点C的仰角为60°,求树高CD(结果精确到0.1米).(参考数据:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4)
如图,某建筑物AB的高为6米,在建筑物顶端A测得一棵树CD的点C的俯角为45°,在地面点B测得点C的仰角为60°,求树高CD(结果精确到0.1米).(参考数据:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4) 分析 根据题意首先表示出AE,BE的长,进而利用$\sqrt{3}$x+x=6,求出答案.
解答 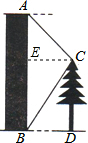 解:作CE⊥AB,垂足为点E,
解:作CE⊥AB,垂足为点E,
在Rt△ACE中,∵∠CAE=45°,
∴设AE=CE=xcm,
在Rt△CBE中,
∵∠CBE=30°,
∴tan∠CBE=$\frac{CE}{BE}$,即$\frac{\sqrt{3}}{3}$=$\frac{x}{BE}$,
∴BE=$\sqrt{3}$x,
∵AE+BE=AB,
∴$\sqrt{3}$x+x=6,
解得:x=$\frac{6}{\sqrt{3}+1}$=3($\sqrt{3}$-1),
∴CD=BE=$\sqrt{3}$x=9-3$\sqrt{3}$≈3.8(m).
答:树高CD约为3.9m.
点评 此题主要考查了解直角三角形的应用,熟练应用锐角三角函数关系是解题关键.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:选择题
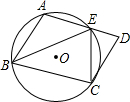 如图,A,B,C是⊙O上一点,四边形ABCD是平行四边形,CD与⊙O相切,AD与⊙O交于点E,∠D=70°,则∠BEC=( )
如图,A,B,C是⊙O上一点,四边形ABCD是平行四边形,CD与⊙O相切,AD与⊙O交于点E,∠D=70°,则∠BEC=( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
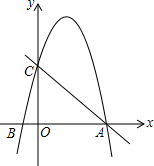 如图,平面直角坐标系xOy中,已知B(-1,0),一次函数y=-x+5的图象与x轴、y轴分别交于点A、C两点,二次函数y=-x2+bx+c的图象经过点A、点B.
如图,平面直角坐标系xOy中,已知B(-1,0),一次函数y=-x+5的图象与x轴、y轴分别交于点A、C两点,二次函数y=-x2+bx+c的图象经过点A、点B.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
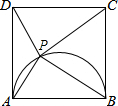 如图,已知四边形ABCD是边长为4的正方形,以AB为直径向正方形内作半圆,P为半圆上一动点(不与A、B重合),当PA=2$\sqrt{2}$或$\frac{8\sqrt{5}}{5}$时,△PAD为等腰三角形.
如图,已知四边形ABCD是边长为4的正方形,以AB为直径向正方形内作半圆,P为半圆上一动点(不与A、B重合),当PA=2$\sqrt{2}$或$\frac{8\sqrt{5}}{5}$时,△PAD为等腰三角形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>b | B. | a=b | C. | a<b | D. | 以上都有可能 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com