
科目:gzsx 来源: 题型:
| 3 |
科目:gzsx 来源: 题型:
| 3 | 2 |
科目:czsx 来源: 题型:解答题
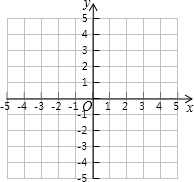 已知直线l1:
已知直线l1: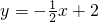 与直线l2:y=2x-3相交于点A.
与直线l2:y=2x-3相交于点A.科目:gzsx 来源: 题型:
| 4 |
| 3 |
| F1A |
| F2B |
科目:czsx 来源: 题型:填空题
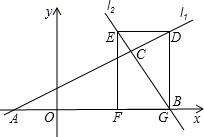 如图,已知直线l1:
如图,已知直线l1: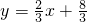 与直线 l2:y=-2x+16相交于点C,直线l1、l2分别交x轴于A、B两点,矩形DEFG的顶点D、E分别在l1、l2上,顶点F、G都在x轴上,且点G与B点重合,那么S矩形DEFG:S△ABC=________.
与直线 l2:y=-2x+16相交于点C,直线l1、l2分别交x轴于A、B两点,矩形DEFG的顶点D、E分别在l1、l2上,顶点F、G都在x轴上,且点G与B点重合,那么S矩形DEFG:S△ABC=________.科目:czsx 来源: 题型:解答题
 如图,已知直线l1:
如图,已知直线l1: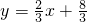 与直线 l2:y=-2x+16相交于点C,直线l1、l2分别交x轴于A、B两点,矩形DEFG的顶点D、E分别在l1、l2上,顶点F、G都在x轴上,且点G与B点重合。
与直线 l2:y=-2x+16相交于点C,直线l1、l2分别交x轴于A、B两点,矩形DEFG的顶点D、E分别在l1、l2上,顶点F、G都在x轴上,且点G与B点重合。
(1)求△ABC的面积;
(2)求矩形DEFG的边DE与EF的长;
(3)若矩形DEFG从原地出发,沿x轴的反方向以每秒1个单位长度的速度平移,设移动时间t(0≤t≤12)秒,矩形DEFG与△ABC重叠部分的面积为S,求S关于t的函数关系式,并写出相应的t的取值范围。
科目:czsx 来源:2013年河北省承德市三沟初中中考数学模拟试卷(解析版) 题型:填空题
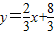 与直线 l2:y=-2x+16相交于点C,直线l1、l2分别交x轴于A、B两点,矩形DEFG的顶点D、E分别在l1、l2上,顶点F、G都在x轴上,且点G与B点重合,那么S矩形DEFG:S△ABC= .
与直线 l2:y=-2x+16相交于点C,直线l1、l2分别交x轴于A、B两点,矩形DEFG的顶点D、E分别在l1、l2上,顶点F、G都在x轴上,且点G与B点重合,那么S矩形DEFG:S△ABC= .
科目:czsx 来源:2012年河北省中考数学模拟试卷(五)(解析版) 题型:填空题
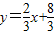 与直线 l2:y=-2x+16相交于点C,直线l1、l2分别交x轴于A、B两点,矩形DEFG的顶点D、E分别在l1、l2上,顶点F、G都在x轴上,且点G与B点重合,那么S矩形DEFG:S△ABC= .
与直线 l2:y=-2x+16相交于点C,直线l1、l2分别交x轴于A、B两点,矩形DEFG的顶点D、E分别在l1、l2上,顶点F、G都在x轴上,且点G与B点重合,那么S矩形DEFG:S△ABC= .
科目:czsx 来源:2011年四川省攀枝花市中考数学试卷(解析版) 题型:填空题
 与直线 l2:y=-2x+16相交于点C,直线l1、l2分别交x轴于A、B两点,矩形DEFG的顶点D、E分别在l1、l2上,顶点F、G都在x轴上,且点G与B点重合,那么S矩形DEFG:S△ABC= .
与直线 l2:y=-2x+16相交于点C,直线l1、l2分别交x轴于A、B两点,矩形DEFG的顶点D、E分别在l1、l2上,顶点F、G都在x轴上,且点G与B点重合,那么S矩形DEFG:S△ABC= .
科目:czsx 来源: 题型:解答题
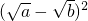 ≥0,∴
≥0,∴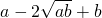 ≥0,∴a+b≥
≥0,∴a+b≥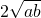 ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.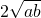 (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥ ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值 .
.  有最小值______;
有最小值______;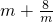 有最小值______.
有最小值______.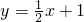 与x轴交于点A,过点A的另一直线L2与双曲线
与x轴交于点A,过点A的另一直线L2与双曲线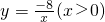 相交于点B(2,m),求直线L2的解析式.
相交于点B(2,m),求直线L2的解析式. 时,点A、B、C、D围成的四边形面积.
时,点A、B、C、D围成的四边形面积.科目:czsx 来源: 题型:
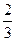 x+
x+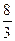 与直线l2:y=2x+16相交于点C,l1,l2分别交x轴于A,B两点.矩形DEFG的顶点D,E分别在直线l1,l2上,顶点F,G都在X轴上,且点G与点B重合.
与直线l2:y=2x+16相交于点C,l1,l2分别交x轴于A,B两点.矩形DEFG的顶点D,E分别在直线l1,l2上,顶点F,G都在X轴上,且点G与点B重合.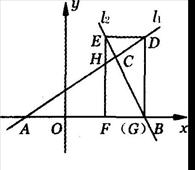
科目:czsx 来源:2010年浙江省初中毕业生学业考试模拟试卷数学卷 题型:解答题
(满分l4分)如图已知直线l1:y=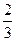 x+
x+ 与直线l2:y=2x+16相交于点C,l1,l2分别交x轴于A,B两点.矩形DEFG的顶点D,E分别在直线l1,l2上,顶点F,G都在X轴上,且点G与点B重合.
与直线l2:y=2x+16相交于点C,l1,l2分别交x轴于A,B两点.矩形DEFG的顶点D,E分别在直线l1,l2上,顶点F,G都在X轴上,且点G与点B重合.
(1)求△ABC的面积;
(2)求矩形DEFG的边DE与EF的长;
(3)若此时矩形DEFG,沿x轴的反方向以每秒l个单位长度的速度平移,设移动时间为t 5(0≤t≤12),矩形DEFG与△ABC重叠部分的面积为S,求S关于t的函数关系式,并写出相应的t的取值范围.
科目:czsx 来源:不详 题型:解答题
 x+
x+ 与直线l2:y=2x+16相交于点C,l1,l2分别交x轴于A,B两点.矩形DEFG的顶点D,E分别在直线l1,l2上,顶点F,G都在X轴上,且点G与点B重合.
与直线l2:y=2x+16相交于点C,l1,l2分别交x轴于A,B两点.矩形DEFG的顶点D,E分别在直线l1,l2上,顶点F,G都在X轴上,且点G与点B重合.
科目:czsx 来源: 题型:
实践与探究:
对于任意正实数a、b,∵![]() ≥0, ∴
≥0, ∴![]() ≥0,∴
≥0,∴![]() ≥
≥![]()
只有当a=b时,等号成立。
结论:在 ≥
≥![]() (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥![]() ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值![]() 。 根据上述内容,回答下列问题:
。 根据上述内容,回答下列问题:
(1)若m>0,只有当m= 时,![]() 有最小值 ;
有最小值 ;
若m>0,只有当m= 时,2![]() 有最小值 .
有最小值 .
(2)如图,已知直线L1:![]() 与x轴交于点A,过点A的另一直线L2与双曲线
与x轴交于点A,过点A的另一直线L2与双曲线![]() 相交于点B(2,m),求直线L2的解析式.
相交于点B(2,m),求直线L2的解析式.

(3)在(2)的条件下,若点C为双曲线上任意一点,作CD∥y轴交直线L1
于点D,试求当线段CD最短时,点A、B、C、D围成的四边形面积.
科目:czsx 来源: 题型:
 ≥0, ∴
≥0, ∴ ≥0,∴
≥0,∴ ≥
≥
 ≥
≥ (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥ ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值 。 根据上述内容,回答下列问题:
。 根据上述内容,回答下列问题: 有最小值 ;
有最小值 ; 有最小值 .
有最小值 . 与x轴交于点A,过点A的另一直线L2与双曲线
与x轴交于点A,过点A的另一直线L2与双曲线 相交于点B(2,m),求直线L2的解析式.
相交于点B(2,m),求直线L2的解析式.
科目:czsx 来源:2011-2012学年江苏省江阴长泾片八年级下学期期中考试数学卷(带解析) 题型:解答题
实践与探究:
对于任意正实数a、b,∵ ≥0, ∴
≥0, ∴ ≥0,∴
≥0,∴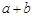 ≥
≥
只有当a=b时,等号成立。
结论:在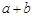 ≥
≥ (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥ ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值 。 根据上述内容,回答下列问题:
。 根据上述内容,回答下列问题:
(1)若m>0,只有当m= 时, 有最小值 ;
有最小值 ;
若m>0,只有当m= 时,2 有最小值 .
有最小值 .
(2)如图,已知直线L1: 与x轴交于点A,过点A的另一直线L2与双曲线
与x轴交于点A,过点A的另一直线L2与双曲线 相交于点B(2,m),求直线L2的解析式.
相交于点B(2,m),求直线L2的解析式.
(3)在(2)的条件下,若点C为双曲线上任意一点,作CD∥y轴交直线L1
于点D,试求当线段CD最短时,点A、B、C、D围成的四边形面积.
科目:czsx 来源:2013届江苏省江阴长泾片八年级下学期期中考试数学卷(解析版) 题型:解答题
实践与探究:
对于任意正实数a、b,∵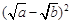 ≥0, ∴
≥0, ∴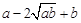 ≥0,∴
≥0,∴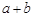 ≥
≥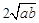
只有当a=b时,等号成立。
结论:在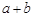 ≥
≥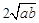 (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥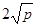 ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值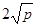 。 根据上述内容,回答下列问题:
。 根据上述内容,回答下列问题:
(1)若m>0,只有当m= 时,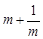 有最小值 ;
有最小值 ;
若m>0,只有当m= 时,2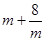 有最小值 .
有最小值 .
(2)如图,已知直线L1: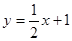 与x轴交于点A,过点A的另一直线L2与双曲线
与x轴交于点A,过点A的另一直线L2与双曲线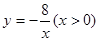 相交于点B(2,m),求直线L2的解析式.
相交于点B(2,m),求直线L2的解析式.
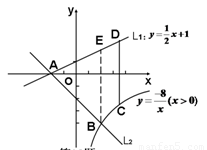
(3)在(2)的条件下,若点C为双曲线上任意一点,作CD∥y轴交直线L1
于点D,试求当线段CD最短时,点A、B、C、D围成的四边形面积.
科目:czsx 来源:不详 题型:解答题
 ≥0, ∴
≥0, ∴ ≥0,∴
≥0,∴ ≥
≥
 ≥
≥ (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥ ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值 。 根据上述内容,回答下列问题:
。 根据上述内容,回答下列问题: 有最小值 ;
有最小值 ; 有最小值 .
有最小值 . 与x轴交于点A,过点A的另一直线L2与双曲线
与x轴交于点A,过点A的另一直线L2与双曲线 相交于点B(2,m),求直线L2的解析式.
相交于点B(2,m),求直线L2的解析式.
科目:czsx 来源: 题型:
 直线l2:y=-
直线l2:y=-| 1 | 2 |
科目:gzsx 来源: 题型: