
科目:czsx 来源: 题型:
科目:czsx 来源: 题型:解答题

科目:czsx 来源:新课标九年级数学竞赛培训第18讲:圆的基本性质(解析版) 题型:解答题
科目:czsx 来源:2007年江苏省泰州市泰兴市横垛初中中考数学模拟试卷(解析版) 题型:解答题
科目:czsx 来源:不详 题型:解答题

科目:czsx 来源:2001年全国中考数学试题汇编《图形的相似》(02)(解析版) 题型:解答题
科目:czsx 来源:2001年全国中考数学试题汇编《圆》(06)(解析版) 题型:解答题
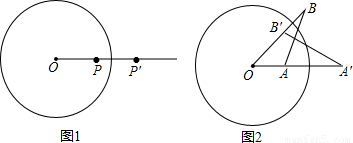
科目:czsx 来源:2001年江苏省南京市中考数学试卷(解析版) 题型:解答题
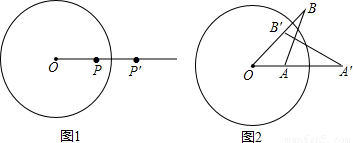
科目:czsx 来源: 题型:解答题
 我们把一个半圆与二次函数图象的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点(半圆与二次函数图象的连接点除外),那么这条直线叫做“蛋圆”的切线.如图,二次函数y=x2-2x-3的图象与x轴交于点A、B,与y轴交于点D,AB为半圆直径,半圆圆心为点M,半圆与y轴的正半轴交于点C.
我们把一个半圆与二次函数图象的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点(半圆与二次函数图象的连接点除外),那么这条直线叫做“蛋圆”的切线.如图,二次函数y=x2-2x-3的图象与x轴交于点A、B,与y轴交于点D,AB为半圆直径,半圆圆心为点M,半圆与y轴的正半轴交于点C.科目:czsx 来源:2013年北京市通州区中考数学一模试卷(解析版) 题型:解答题

科目:czsx 来源:2013年福建省泉州市中考数学模拟试卷(三)(解析版) 题型:解答题

科目:czsx 来源: 题型:
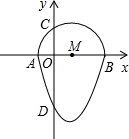 (2013•通州区一模)我们把一个半圆与二次函数图象的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点(半圆与二次函数图象的连接点除外),那么这条直线叫做“蛋圆”的切线.如图,二次函数y=x2-2x-3的图象与x轴交于点A、B,与y轴交于点D,AB为半圆直径,半圆圆心为点M,半圆与y轴的正半轴交于点C.
(2013•通州区一模)我们把一个半圆与二次函数图象的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点(半圆与二次函数图象的连接点除外),那么这条直线叫做“蛋圆”的切线.如图,二次函数y=x2-2x-3的图象与x轴交于点A、B,与y轴交于点D,AB为半圆直径,半圆圆心为点M,半圆与y轴的正半轴交于点C.科目:czsx 来源:同步练习 数学九年级下册 题型:044
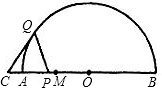
如图,AB是半圆O的直径,点M是半径OA的中点,点P在线段AM上运动(不与点M重合),点Q在半圆O上运动,且总保持PQ=PO,过点Q作⊙O的切线交BA的延长线于点C.
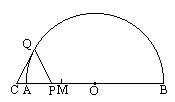
(1)当∠QPA=![]() 时,请你对△QCP的形状做出猜想,并给予证明;
时,请你对△QCP的形状做出猜想,并给予证明;
(2)当QP⊥AB时,△QCP的形状是________三角形;
(3)由(1)(2)得出的结论,请进一步猜想当点P在线段AM上运动到任何位置时,△QCP一定是________三角形.
科目:czsx 来源:三点一测丛书九年级数学上 题型:044
如图,AB是半圆O的直径,点M是半径OA的中点,点P在线段AM上运动,且总保持PQ=PO,过点Q作![]() O的切线交BA的延长线于点C.
O的切线交BA的延长线于点C.

(1)当∠QPA=![]() 时,请你对△QCP的形状做出猜想,并给予证明;
时,请你对△QCP的形状做出猜想,并给予证明;
(2)当QP⊥AB时,△QCP的形状是何种三角形,并说明理由;
(3)由(1)、(2)得出结论,请进一步猜想当点P在线段AM上运动到任何位置时,△QCP一定是何种三角形?
科目:czsx 来源: 题型:044
如图,AB是半圆O的直径,点M是半径OA的中点,点P在线段AM上运动(不与点M重合),点Q在半圆O上运动,且总保持PQ=PO,过点Q作⊙O的切线交BA的延长线于点C.

(1)当∠QPA=60°时,请你对△QCP的形状做出猜想,并给予说明.
(2)当PQ⊥AB时,△QCP的形状是________三角形.
(3)由(1)(2)得出的结论,请进一步猜想当点P在线段AM上运动到任何位置时,△QCP一定是________三角形.
科目:czsx 来源: 题型:解答题
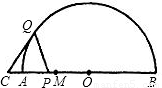
 CP一定是______三角形.
CP一定是______三角形.科目:czsx 来源:《第3章 直线和圆、圆和圆的位置关系》2009年单元测试(解析版) 题型:解答题

科目:czsx 来源:《第24章 圆》2009年综合能力测试(解析版) 题型:解答题

科目:czsx 来源:2006年浙江省宁波市昆山高中实验班招生考试数学试卷(解析版) 题型:解答题
科目:czsx 来源:不详 题型:解答题
 CP一定是______三角形.
CP一定是______三角形.