如图.在△ABC中∠C=90.D是BC的中点.且∠ADC答案解析
科目:czsx
来源:
题型:
如图,在直角梯形ABCD中,DC∥AB,∠ADC=90°,AB=3a,CD=2a,AD=2,点E、F分别是腰AD、

BC上的动点,点G在AB上,且四边形AEFG是矩形.设FG=x,矩形AEFG的面积为y.
(1)求y与x之间的函数关式,并写出自变量x的取值范围;
(2)在腰BC上求一点F,使梯形ABCD的面积是矩形AEFG的面积的2倍,并求出此时BF的长;
(3)当∠ABC=60°时,矩形AEFG能否为正方形?若能,求出其边长;若不能,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.
(1)当直线MN绕点C旋转到如图1的位置时,
①通过观察、猜想,△ADC和△CEB的关系是:______;
②猜想DE、AD、BE三者之间满足的数量关系是:______;
③请证明你的上述两个猜想.
(2)当直线MN绕着点C顺时针旋转到MN与AB相交于点F(AF>BF)的位置(如图2所示)时,请直接写出下列问题的答案:
①请你判断△ADC和△CEB还具有(1)中①的关系吗?
②猜想DE、AD、BE三者之间具有怎样的数量关系.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图,在直角梯形ABCD中,DC∥AB,∠ADC=90°,AB=3a,CD=2a,AD=2,点E、F分别是腰AD、 BC上的动点,点G在AB上,且四边形AEFG是矩形.设FG=x,矩形AEFG的面积为y.
BC上的动点,点G在AB上,且四边形AEFG是矩形.设FG=x,矩形AEFG的面积为y.
(1)求y与x之间的函数关式,并写出自变量x的取值范围;
(2)在腰BC上求一点F,使梯形ABCD的面积是矩形AEFG的面积的2倍,并求出此时BF的长;
(3)当∠ABC=60°时,矩形AEFG能否为正方形?若能,求出其边长;若不能,请说明理由.
查看答案和解析>>
科目:czsx
来源:河北省期末题
题型:解答题
在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.(1)当直线MN绕点C旋转到如图1的位置时,
①通过观察、猜想,△ADC和△CEB的关系是: ;
②猜想DE、AD、BE三者之间满足的数量关系是: ;
③请证明你的上述两个猜想.
(2)当直线MN绕着点C顺时针旋转到MN与AB相交于点F(AF>BF)的位置(如图2所示)时,请直接写出下列问题的答案:
①请你判断△ADC和△CEB还具有(1)中①的关系吗?
②猜想DE、AD、BE三者之间具有怎样的数量关系.
查看答案和解析>>
科目:czsx
来源:2008-2009学年四川省成都市九年级(上)期末数学试卷(解析版)
题型:解答题
如图,在直角梯形ABCD中,DC∥AB,∠ADC=90°,AB=3a,CD=2a,AD=2,点E、F分别是腰AD、BC上的动点,点G在AB上,且四边形AEFG是矩形.设FG=x,矩形AEFG的面积为y.
(1)求y与x之间的函数关式,并写出自变量x的取值范围;
(2)在腰BC上求一点F,使梯形ABCD的面积是矩形AEFG的面积的2倍,并求出此时BF的长;
(3)当∠ABC=60°时,矩形AEFG能否为正方形?若能,求出其边长;若不能,请说明理由.

查看答案和解析>>
科目:czsx
来源:不详
题型:解答题
如图,在直角梯形ABCD中,DC
∥AB,∠ADC=90°,AB=3a,CD=2a,AD=2,点E、F分别是腰AD、

BC上的动点,点G在AB上,且四边形AEFG是矩形.设FG=x,矩形AEFG的面积为y.
(1)求y与x之间的函数关式,并写出自变量x的取值范围;
(2)在腰BC上求一点F,使梯形ABCD的面积是矩形AEFG的面积的2倍,并求出此时BF的长;
(3)当∠ABC=60°时,矩形AEFG能否为正方形?若能,求出其边长;若不能,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
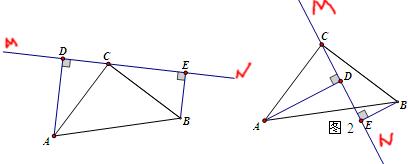
27、在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.
(1)当直线MN绕点C旋转到如图1的位置时,
①通过观察、猜想,△ADC和△CEB的关系是:
△ADC≌△CEB
;
②猜想DE、AD、BE三者之间满足的数量关系是:
DE=AD+BE
;
③请证明你的上述两个猜想.
(2)当直线MN绕着点C顺时针旋转到MN与AB相交于点F(AF>BF)的位置(如图2所示)时,请直接写出下列问题的答案:
①请你判断△ADC和△CEB还具有(1)中①的关系吗?
②猜想DE、AD、BE三者之间具有怎样的数量关系.
查看答案和解析>>
科目:czsx
来源:
题型:
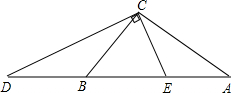
如图,在△ABC中,∠ACB=90°,D是AB延长线上一点,且BD=BC,CE⊥CD交AB于E.
(1)求证:△ACE∽△ADC;
(2)若BE:EA=3:2,求sin∠A的值.
查看答案和解析>>
科目:czsx
来源:
题型:
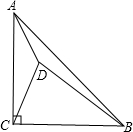
如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D为△ABC内一点,AD=1,而DC、DB的长是关于x的方程x
2-kx+6=0的两个实数根x
1,x
2(DC<DB)并且
+=.
(1)作出△ACD绕点C顺时针旋转90°后所得△BCE;
(2)求k的值,并连接DE并说明△DCE的形状;
(3)求∠ADC的度数.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:
①△AED≌△AEF;②
=
;③△ABC的面积等于四边形AFBD的面积;
④BE
2+DC
2=DE
2 ⑤BE+DC=DE
其中正确的是( )
查看答案和解析>>
科目:czsx
来源:
题型:
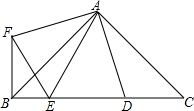
如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:
①△AED≌△AEF;②△ABE≌△ACD;③BE
2+DC
2=DE
2;④
=.
其中正确的是( )
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在△ABC中,∠ACB=90°,点D是BC的中点,且∠B+∠ADC=90°,过点B、D作⊙O,使圆心D在AB上,⊙O交AB于点E.
(1)求证:直线AD与⊙0相切;
(2)若AC=6,求AE的长.
查看答案和解析>>
科目:czsx
来源:
题型:
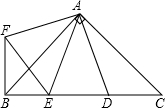
如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕A顺时针旋转90°后,得到△AFB,连结EF,则下列结论正确的个数有( )
①∠EAF=45°;②△EBF为等腰直角三角形;③EA平分∠CEF;④BE
2+CD
2=ED
2.
查看答案和解析>>
科目:czsx
来源:
题型:
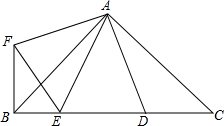
如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:(1)△AED≌△AEF;(2)△ABE∽△ACD;(3)BE+DC=DE;(4)BE
2+DC
2=DE
2.其中正确的是( )
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在△ABC中,∠ACB=90°,O为BC边上一点,以O为圆心,OB为半径作半圆与AB边和BC边分别交于点D、点E,连接CD,且CD=CA,BD=
6,tan∠ADC=2.
(1)求证:CD是半圆O的切线;
(2)求半圆O的直径;
(3)求AD的长.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在Rt△ABC中,∠B=90°,D是BC延长线上的一点,且CD=CA,∠ADC=15°,若AB=3cm,则CD=
6
6
cm.
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在△ABC中,∠C=90°,D是边BC上一点,且∠ADC=60°,那么下列说法中错误的是( )
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:
①△AED≌△AEF;
②△ABE∽△ACD;
③BE+DC=DE;
④BE
2+DC
2=DE
2.
其中一定正确的是( )
查看答案和解析>>
科目:czsx
来源:数学教研室
题型:047
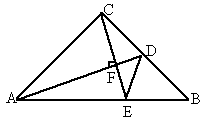
如图所示,在△ABC中,∠ACB=90°,∠B=45°,且AC=BC,AD是BC边上的中线,过C作AD的垂线交AB于点C,交AD于点F,连接DE.
求证:∠ADC=∠BDE.
查看答案和解析>>
科目:czsx
来源:学习周报 数学 北大师八年级版 2009-2010学年 第6期 总第162期 北师大版
题型:013
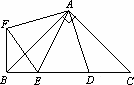
如图,在
Rt
△ABC
中,AB
=AC
,D
、E
是斜边BC
上两点,且∠DAE
=45
°,将△ADC
绕点A
顺时针旋转90
°后,得到△AFB
,连接EF
,下列结论:
①△
AED
≌△AEF
;
②
BE
+DC
=DE
;
③
BE
2+DC
2=DE
2.其中正确的有
[ ]
查看答案和解析>>

 BC上的动点,点G在AB上,且四边形AEFG是矩形.设FG=x,矩形AEFG的面积为y.
BC上的动点,点G在AB上,且四边形AEFG是矩形.设FG=x,矩形AEFG的面积为y.
 BC上的动点,点G在AB上,且四边形AEFG是矩形.设FG=x,矩形AEFG的面积为y.
BC上的动点,点G在AB上,且四边形AEFG是矩形.设FG=x,矩形AEFG的面积为y.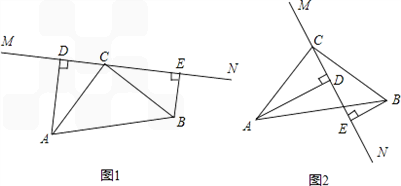

 BC上的动点,点G在AB上,且四边形AEFG是矩形.设FG=x,矩形AEFG的面积为y.
BC上的动点,点G在AB上,且四边形AEFG是矩形.设FG=x,矩形AEFG的面积为y.
 如图,在△ABC中,∠ACB=90°,D是AB延长线上一点,且BD=BC,CE⊥CD交AB于E.
如图,在△ABC中,∠ACB=90°,D是AB延长线上一点,且BD=BC,CE⊥CD交AB于E. 如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D为△ABC内一点,AD=1,而DC、DB的长是关于x的方程x2-kx+6=0的两个实数根x1,x2(DC<DB)并且
如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D为△ABC内一点,AD=1,而DC、DB的长是关于x的方程x2-kx+6=0的两个实数根x1,x2(DC<DB)并且 如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:
如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论: 如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:
如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论: 如图,在△ABC中,∠ACB=90°,点D是BC的中点,且∠B+∠ADC=90°,过点B、D作⊙O,使圆心D在AB上,⊙O交AB于点E.
如图,在△ABC中,∠ACB=90°,点D是BC的中点,且∠B+∠ADC=90°,过点B、D作⊙O,使圆心D在AB上,⊙O交AB于点E. 如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕A顺时针旋转90°后,得到△AFB,连结EF,则下列结论正确的个数有( )
如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕A顺时针旋转90°后,得到△AFB,连结EF,则下列结论正确的个数有( ) 如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:(1)△AED≌△AEF;(2)△ABE∽△ACD;(3)BE+DC=DE;(4)BE2+DC2=DE2.其中正确的是( )
如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:(1)△AED≌△AEF;(2)△ABE∽△ACD;(3)BE+DC=DE;(4)BE2+DC2=DE2.其中正确的是( ) 如图,在△ABC中,∠ACB=90°,O为BC边上一点,以O为圆心,OB为半径作半圆与AB边和BC边分别交于点D、点E,连接CD,且CD=CA,BD=6
如图,在△ABC中,∠ACB=90°,O为BC边上一点,以O为圆心,OB为半径作半圆与AB边和BC边分别交于点D、点E,连接CD,且CD=CA,BD=6 如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:
如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:
