
科目:czsx 来源: 题型:
在平面直角坐标系中△ABC的边AB在x轴上,且OA>OB,以AB为直径的圆过点C
若C的坐标为(0,2),AB=5, A,B两点的横坐标XA,XB是关于X的方程![]() 的两根:
的两根:
(1) 求m,n的值
(2) 若∠ACB的平分线所在的直线![]() 交x轴于点D,试求直线
交x轴于点D,试求直线![]() 对应的一次函数的解析式
对应的一次函数的解析式
科目:czsx 来源: 题型:
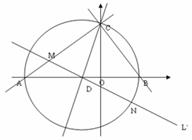
在平面直角坐标系中△ABC的边AB在x轴上,且OA>OB,以AB为直径的圆过点C,若C的坐标为(0,2),AB=5,A,B两点的横坐标XA,XB是关于X的方程的两根:
1.求m,n的值;
2.若∠ACB的平分线所在的直线交x轴于点D,试求直线
对应的一次函数的解析式;
3.过点D任作一直线分别交射线CA,CB(点C除外)于点M,N,则
的值是否为定值,若是,求出定值,若不是,请说明理由
科目:czsx 来源: 题型:
 的两根:
的两根:
 交x轴于点D,试求直线
交x轴于点D,试求直线 对应的一次函数的解析式;
对应的一次函数的解析式; 分别交射线CA,CB(点C除外)于点M,N,则
分别交射线CA,CB(点C除外)于点M,N,则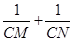 的值是否为定值,若是,求出定值,若不是,请说明理由
的值是否为定值,若是,求出定值,若不是,请说明理由 科目:czsx 来源:2012-2013学年浙江省杭州市萧山区新围初中八年级第二次月考数学试卷(带解析) 题型:解答题
在平面直角坐标系中, △ABC的三个顶点的位置如图所示,点A'的坐标是
(-2,2), 现将△ABC平移,使点A变换为点A',点B′、C′分别是B、C的对应点。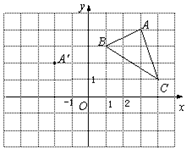
(1)请画出平移后的像△A'B'C'(不写画法) ,并直接写出点B′、C′的坐标:
B′ ( ) 、C′ ( ) ;
(2)若△ABC 内部一点P的坐标为(a,b),则点P 的对应点P ′的坐标是 ( ) .
科目:czsx 来源:2014届浙江省杭州市八年级第二次月考数学试卷(解析版) 题型:解答题
在平面直角坐标系中, △ABC的三个顶点的位置如图所示,点A'的坐标是
(-2,2), 现将△ABC平移,使点A变换为点A',点B′、C′分别是B、C的对应点。

(1)请画出平移后的像△A'B'C'(不写画法) ,并直接写出点B′、C′的坐标:
B′ ( ) 、C′ ( ) ;
(2)若△ABC 内部一点P的坐标为(a,b),则点P 的对应点P ′的坐标是 ( ) .
科目:czsx 来源:2010-2011学年福建莆田秀屿区实验中学中考模拟数学试卷 题型:解答题
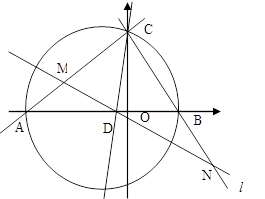
在平面直角坐标系中△ABC的边AB在x轴上,且OA>OB,以AB为直径的圆过点C,若C的坐标为(0,2),AB=5,
A,B两点的横坐标XA,XB是关于X的方程 的两根:
的两根:

1.求m,n的值;
2.若∠ACB的平分线所在的直线 交x轴于点D,试求直线
交x轴于点D,试求直线 对应的一次函数的解析式;
对应的一次函数的解析式;
3.过点D任作一直线 分别交射线CA,CB(点C除外)于点M,N,则
分别交射线CA,CB(点C除外)于点M,N,则 的值是否为定值,若是,求出定值,若不是,请说明理由
的值是否为定值,若是,求出定值,若不是,请说明理由
科目:czsx 来源:不详 题型:解答题
 的两根:
的两根:
 交x轴于点D,试求直线
交x轴于点D,试求直线 对应的一次函数的解析式;
对应的一次函数的解析式; 分别交射线CA,CB(点C除外)于点M,N,则
分别交射线CA,CB(点C除外)于点M,N,则 的值是否为定值,若是,求出定值,若不是,请说明理由
的值是否为定值,若是,求出定值,若不是,请说明理由科目:czsx 来源: 题型:
在平面直角坐标系中, △ABC的三个顶点的位置如图所示,点A'的坐标是(-2,2), 现将△ABC平移,使点A变换为点A', 点B′、C′分别是B、C的对应点.

(1)请画出平移后的像△A'B'C'(不写画法) ,并直接写出点B′、C′的坐标: B′ ( ) 、C′ ( ) ;
(2)若△ABC 内部一点P的坐标为(a,b),则点P的对应点P ′的坐标是 ( ) .
科目:czsx 来源:不详 题型:解答题

科目:czsx 来源: 题型:
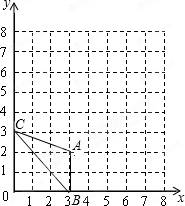 在平面直角坐标系中△ABC的三个顶点坐标分别为A(3,2)、B(3,0)、C(0,3).画出一个以原点O为位似中心,△ABC放大2倍的△A1B1C1,并且写出A1的坐标.
在平面直角坐标系中△ABC的三个顶点坐标分别为A(3,2)、B(3,0)、C(0,3).画出一个以原点O为位似中心,△ABC放大2倍的△A1B1C1,并且写出A1的坐标.科目:czsx 来源: 题型:
在平面直角坐标系中△ABC的边AB在x轴上,且OA>OB,以AB为直径的 过点C,若C的坐标为(0,2),AB=5, 经过A、B、C三点的抛物线为y=ax2+bx+c。
过点C,若C的坐标为(0,2),AB=5, 经过A、B、C三点的抛物线为y=ax2+bx+c。
(1)求点A、B的坐标及抛物线的解析式。
(2)若∠ACB的平分线所在的直线 交x轴于点D,交圆于点E。
交x轴于点D,交圆于点E。
①求证:PE⊥x轴;
②试求直线 对应的一次函数的解析式.
对应的一次函数的解析式.
(3)过点D任作一直线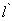 分别交射线CA,CB(点C除外)于点M,N,则
分别交射线CA,CB(点C除外)于点M,N,则 的值是否为定值,若是,求出定值,若不是,请说明理由
的值是否为定值,若是,求出定值,若不是,请说明理由
 |
科目:czsx 来源: 题型:
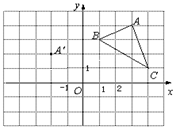
科目:czsx 来源:2011-2012学年浙江省杭州市萧山临浦片八年级12月月考数学卷 题型:解答题
(本题6分) 在平面直角坐标系中, △ABC的三个顶点的位置如图所示,点A'的坐标是(-2,2), 现将△ABC平移,使点A变换为点A',点B′、C′分别是B、C的对应点.
【小题1】(1)请画出平移后的像△A'B'C'(不写画法) ,
并直接写出点B′、C′的坐标:
B′( ) 、C′ ( ) ;
【小题2】(2)若△ABC 内部一点P的坐标为(a,b),则点P
的对应点P ′的坐标是 ( ) .
科目:czsx 来源:2013届浙江省杭州市萧山临浦片八年级12月月考数学卷 题型:解答题
(本题6分) 在平面直角坐标系中, △ABC的三个顶点的位置如图所示,点A'的坐标是(-2,2), 现将△ABC平移,使点A变换为点A', 点B′、C′分别是B、C的对应点.
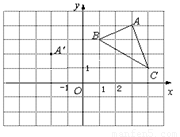
1.(1)请画出平移后的像△A'B'C'(不写画法) ,
并直接写出点B′、C′的坐标:
B′( ) 、C′ ( ) ;
2.(2)若△ABC 内部一点P的坐标为(a,b),则点P
的对应点P ′的坐标是 ( ) .
科目:czsx 来源: 题型:
(本题6分) 在平面直角坐标系中, △ABC的三个顶点的位置如图所示,点A'的坐标是(-2,2), 现将△ABC平移,使点A变换为点A', 点B′、C′分别是B、C的对应点.
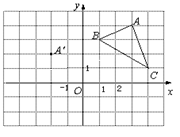
1.(1)请画出平移后的像△A'B'C'(不写画法) ,
并直接写出点B′、C′的坐标:
B′( ) 、C′ ( ) ;
2.(2)若△ABC 内部一点P的坐标为(a,b),则点P
的对应点P ′的坐标是( ) .
科目:czsx 来源:数学教研室 题型:013
A.△DEF由△ABC绕0点顺时针旋转![]() 得到
得到
B.△DEF由△ABC绕0点逆时针旋转![]() 得到
得到
C.△DEF由△ABC绕0点顺时针旋转![]() 得到
得到
D.△DEF由△ABC绕0点顺时针旋转![]() 得到
得到
科目:czsx 来源: 题型:
| 1 | 4 |
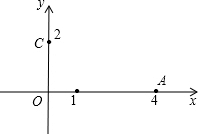 ,0)、C(0,2).
,0)、C(0,2).科目:czsx 来源: 题型:
科目:czsx 来源: 题型:
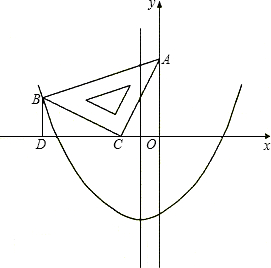 靠在两坐标轴上,点C为(-1,0).如图所示,B点在抛物线y=
靠在两坐标轴上,点C为(-1,0).如图所示,B点在抛物线y=| 1 |
| 2 |
| 1 |
| 2 |