在代数式ax2+bx+c中.x分别取0 1 -1答案解析
科目:czsx
来源:
题型:解答题
 已知二次函数y=ax2+bx+2,它的图象经过点(1,2).
已知二次函数y=ax2+bx+2,它的图象经过点(1,2).
(1)如果用含a的代数式表示b,那么b=______;
(2)如图所示,如果该图象与x轴的一个交点为(-1,0).
①求二次函数的表达式,并写出图象的顶点坐标;
②在平面直角坐标系中,如果点P到x轴与y轴的距离相等,则称点P为等距点.求出这个二次函数图象上所有等距点的坐标.
(3)当a取a1,a2时,二次函数图象与x轴正半轴分别交于点M(m,0),点N(n,0).如果点N在点M的右边,且点M和点N都在点(1,0)的右边.试比较a1和a2的大小.
查看答案和解析>>
科目:czsx
来源:
题型:
已知二次函数y=ax2+bx+2,它的图像经过点(1,2).
1.如果用含a的代数式表示b,那么b= ;
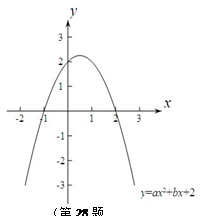
2.如图所示,如果该图像与x轴的一个交点为(-1,0).
① 求二次函数的表达式,并写出图像的顶点坐标;
②在平面直角坐标系中,如果点P到x轴与y轴的距离相等,则称点P为等距点.求出这个二次函数图像上所有等距点的坐标.
3.当a取a1,a2时,二次函数图像与x轴正半轴分别交于点M(m,0),点N(n,0).如果点N在点M的右边,且点M和点N都在点(1,0)的右边.试比较a1和a2的大小.
查看答案和解析>>
科目:czsx
来源:
题型:
已知二次函数y=ax
2+bx+2,它的图像经过点(1,2).
【小题1】如果用含a的代数式表示b,那么b=
;
【小题2】如图所示,如果该图像与x轴的一个交点为(-1,0).
① 求二次函数的表达式,并写出图像的顶点坐标;
②在平面直角坐标系中,如果点P到x轴与y轴的距离相等,则称点P为等距点.求出这个二次函数图像上所有等距点的坐标.
【小题3】当a取a
1,a
2时,二次函数图像与x轴正半轴分别交于点M(m,0),点N(n,0).如果点N在点M的右边,且点M和点N都在点(1,0)的右边.试比较a
1和a
2的大小.

查看答案和解析>>
科目:czsx
来源:2012届江苏省南京市建邺区中考一模数学试卷(带解析)
题型:解答题
已知二次函数y=ax2+bx+2,它的图像经过点(1,2).
【小题1】如果用含a的代数式表示b,那么b= ;
【小题2】如图所示,如果该图像与x轴的一个交点为(-1,0).
① 求二次函数的表达式,并写出图像的顶点坐标;
②在平面直角坐标系中,如果点P到x轴与y轴的距离相等,则称点P为等距点.求出这个二次函数图像上所有等距点的坐标.
【小题3】当a取a1,a2时,二次函数图像与x轴正半轴分别交于点M(m,0),点N(n,0).如果点N在点M的右边,且点M和点N都在点(1,0)的右边.试比较a1和a2的大小.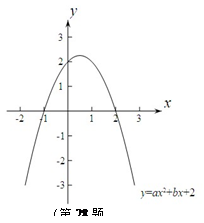
查看答案和解析>>
科目:czsx
来源:2012年北京市大兴区中考数学二模试卷(解析版)
题型:解答题
已知二次函数y=ax
2+bx+2,它的图象经过点(1,2).
(1)如果用含a的代数式表示b,那么b=______;
(2)如图所示,如果该图象与x轴的一个交点为(-1,0).
①求二次函数的表达式,并写出图象的顶点坐标;
②在平面直角坐标系中,如果点P到x轴与y轴的距离相等,则称点P为等距点.求出这个二次函数图象上所有等距点的坐标.
(3)当a取a
1,a
2时,二次函数图象与x轴正半轴分别交于点M(m,0),点N(n,0).如果点N在点M的右边,且点M和点N都在点(1,0)的右边.试比较a
1和a
2的大小.

查看答案和解析>>
科目:czsx
来源:2012年山西省中考数学模拟试卷(七)(解析版)
题型:解答题
已知二次函数y=ax
2+bx+2,它的图象经过点(1,2).
(1)如果用含a的代数式表示b,那么b=______;
(2)如图所示,如果该图象与x轴的一个交点为(-1,0).
①求二次函数的表达式,并写出图象的顶点坐标;
②在平面直角坐标系中,如果点P到x轴与y轴的距离相等,则称点P为等距点.求出这个二次函数图象上所有等距点的坐标.
(3)当a取a
1,a
2时,二次函数图象与x轴正半轴分别交于点M(m,0),点N(n,0).如果点N在点M的右边,且点M和点N都在点(1,0)的右边.试比较a
1和a
2的大小.
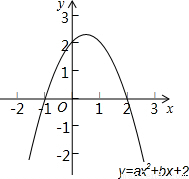
查看答案和解析>>
科目:czsx
来源:2012年江苏省南京市建邺区中考数学一模试卷(解析版)
题型:解答题
已知二次函数y=ax
2+bx+2,它的图象经过点(1,2).
(1)如果用含a的代数式表示b,那么b=______;
(2)如图所示,如果该图象与x轴的一个交点为(-1,0).
①求二次函数的表达式,并写出图象的顶点坐标;
②在平面直角坐标系中,如果点P到x轴与y轴的距离相等,则称点P为等距点.求出这个二次函数图象上所有等距点的坐标.
(3)当a取a
1,a
2时,二次函数图象与x轴正半轴分别交于点M(m,0),点N(n,0).如果点N在点M的右边,且点M和点N都在点(1,0)的右边.试比较a
1和a
2的大小.
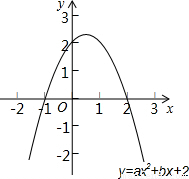
查看答案和解析>>
科目:czsx
来源:2011-2012学年江苏省南京市建邺区中考一模数学试卷(解析版)
题型:解答题
已知二次函数y=ax2+bx+2,它的图像经过点(1,2).
1.如果用含a的代数式表示b,那么b= ;
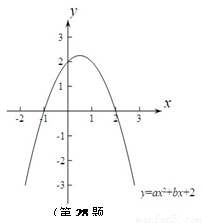
2.如图所示,如果该图像与x轴的一个交点为(-1,0).
① 求二次函数的表达式,并写出图像的顶点坐标;
②在平面直角坐标系中,如果点P到x轴与y轴的距离相等,则称点P为等距点.求出这个二次函数图像上所有等距点的坐标.
3.当a取a1,a2时,二次函数图像与x轴正半轴分别交于点M(m,0),点N(n,0).如果点N在点M的右边,且点M和点N都在点(1,0)的右边.试比较a1和a2的大小.
查看答案和解析>>
科目:czsx
来源:2013-2014学年江苏省中考模拟数学试卷(解析版)
题型:解答题
已知二次函数y=ax2+bx+2,它的图象经过点(1,2).
(1)如果用含a的代数式表示b,那么b= ;
(2)如图所示,如果该图象与x轴的一个交点为(﹣1,0).

①求二次函数的表达式,并写出图象的顶点坐标;
②在平面直角坐标系中,如果点P到x轴与y轴的距离相等,则称点P为等距点.求出这个二次函数图象上所有等距点的坐标.
(3)当a取a1,a2时,二次函数图象与x轴正半轴分别交于点M(m,0),点N(n,0).如果点N在点M的右边,且点M和点N都在点(1,0)的右边.试比较a1和a2的大小.
查看答案和解析>>
科目:czsx
来源:
题型:

(2012•大兴区二模)已知二次函数y=ax
2+bx+2,它的图象经过点(1,2).
(1)如果用含a的代数式表示b,那么b=
-a
-a
;
(2)如图所示,如果该图象与x轴的一个交点为(-1,0).
①求二次函数的表达式,并写出图象的顶点坐标;
②在平面直角坐标系中,如果点P到x轴与y轴的距离相等,则称点P为等距点.求出这个二次函数图象上所有等距点的坐标.
(3)当a取a
1,a
2时,二次函数图象与x轴正半轴分别交于点M(m,0),点N(n,0).如果点N在点M的右边,且点M和点N都在点(1,0)的右边.试比较a
1和a
2的大小.
查看答案和解析>>
科目:czsx
来源:2006年天津市初中毕业生学业考试数学试卷
题型:044
已知抛物线y=ax2+bx+c的定点坐标为(2,4).
(Ⅰ)试用含a的代数式分别表示b,c;
(Ⅱ)若直线y=kx+4(k≠0)与y轴及该抛物线的交点依次为D、E、F,且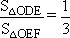 ,其中O为坐标原点,试用含a的代数式表示k;
,其中O为坐标原点,试用含a的代数式表示k;
(Ⅲ)在(Ⅱ)的条件下,若线段EF的长m满足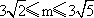 ,试确定a的取值范围.
,试确定a的取值范围.
查看答案和解析>>
科目:czsx
来源:
题型:
已知抛物线y=ax
2+bx+c的顶点坐标为(2,4).
(Ⅰ)试用含a的代数式分别表示b,c;
(Ⅱ)若直线y=kx+4(k≠0)与y轴及该抛物线的交点依次为D、E、F,且
=,其中O为坐标原点,试用含a的代数式表示k;
(Ⅲ)在(Ⅱ)的条件下,若线段EF的长m满足3
≤m≤3
,试确定a的取值范围.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
已知抛物线y=ax2+bx+c的顶点坐标为(2,4).
(Ⅰ)试用含a的代数式分别表示b,c;
(Ⅱ)若直线y=kx+4(k≠0)与y轴及该抛物线的交点依次为D、E、F,且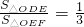 ,其中O为坐标原点,试用含a的代数式表示k;
,其中O为坐标原点,试用含a的代数式表示k;
(Ⅲ)在(Ⅱ)的条件下,若线段EF的长m满足3 ≤m≤3
≤m≤3 ,试确定a的取值范围.
,试确定a的取值范围.
查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(42):2.7 最大面积是多少(解析版)
题型:解答题
已知抛物线y=ax
2+bx+c的顶点坐标为(2,4).
(Ⅰ)试用含a的代数式分别表示b,c;
(Ⅱ)若直线y=kx+4(k≠0)与y轴及该抛物线的交点依次为D、E、F,且
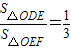
,其中O为坐标原点,试用含a的代数式表示k;
(Ⅲ)在(Ⅱ)的条件下,若线段EF的长m满足3

≤m≤3
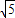
,试确定a的取值范围.
查看答案和解析>>
科目:czsx
来源:第6章《二次函数》中考题集(45):6.4 二次函数的应用(解析版)
题型:解答题
已知抛物线y=ax
2+bx+c的顶点坐标为(2,4).
(Ⅰ)试用含a的代数式分别表示b,c;
(Ⅱ)若直线y=kx+4(k≠0)与y轴及该抛物线的交点依次为D、E、F,且
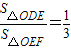
,其中O为坐标原点,试用含a的代数式表示k;
(Ⅲ)在(Ⅱ)的条件下,若线段EF的长m满足3
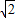
≤m≤3
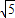
,试确定a的取值范围.
查看答案和解析>>
科目:czsx
来源:第27章《二次函数》中考题集(44):27.3 实践与探索(解析版)
题型:解答题
已知抛物线y=ax
2+bx+c的顶点坐标为(2,4).
(Ⅰ)试用含a的代数式分别表示b,c;
(Ⅱ)若直线y=kx+4(k≠0)与y轴及该抛物线的交点依次为D、E、F,且
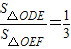
,其中O为坐标原点,试用含a的代数式表示k;
(Ⅲ)在(Ⅱ)的条件下,若线段EF的长m满足3
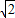
≤m≤3

,试确定a的取值范围.
查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(46):2.8 二次函数的应用(解析版)
题型:解答题
已知抛物线y=ax
2+bx+c的顶点坐标为(2,4).
(Ⅰ)试用含a的代数式分别表示b,c;
(Ⅱ)若直线y=kx+4(k≠0)与y轴及该抛物线的交点依次为D、E、F,且
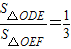
,其中O为坐标原点,试用含a的代数式表示k;
(Ⅲ)在(Ⅱ)的条件下,若线段EF的长m满足3
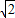
≤m≤3
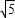
,试确定a的取值范围.
查看答案和解析>>
科目:czsx
来源:第20章《二次函数和反比例函数》中考题集(41):20.5 二次函数的一些应用(解析版)
题型:解答题
已知抛物线y=ax
2+bx+c的顶点坐标为(2,4).
(Ⅰ)试用含a的代数式分别表示b,c;
(Ⅱ)若直线y=kx+4(k≠0)与y轴及该抛物线的交点依次为D、E、F,且

,其中O为坐标原点,试用含a的代数式表示k;
(Ⅲ)在(Ⅱ)的条件下,若线段EF的长m满足3

≤m≤3

,试确定a的取值范围.
查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(42):2.4 二次函数的应用(解析版)
题型:解答题
已知抛物线y=ax
2+bx+c的顶点坐标为(2,4).
(Ⅰ)试用含a的代数式分别表示b,c;
(Ⅱ)若直线y=kx+4(k≠0)与y轴及该抛物线的交点依次为D、E、F,且
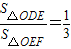
,其中O为坐标原点,试用含a的代数式表示k;
(Ⅲ)在(Ⅱ)的条件下,若线段EF的长m满足3

≤m≤3

,试确定a的取值范围.
查看答案和解析>>
科目:czsx
来源:第23章《二次函数与反比例函数》中考题集(41):23.5 二次函数的应用(解析版)
题型:解答题
已知抛物线y=ax
2+bx+c的顶点坐标为(2,4).
(Ⅰ)试用含a的代数式分别表示b,c;
(Ⅱ)若直线y=kx+4(k≠0)与y轴及该抛物线的交点依次为D、E、F,且
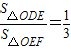
,其中O为坐标原点,试用含a的代数式表示k;
(Ⅲ)在(Ⅱ)的条件下,若线段EF的长m满足3

≤m≤3

,试确定a的取值范围.
查看答案和解析>>

 已知二次函数y=ax2+bx+2,它的图象经过点(1,2).
已知二次函数y=ax2+bx+2,它的图象经过点(1,2).



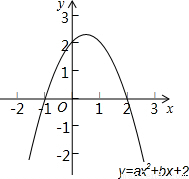
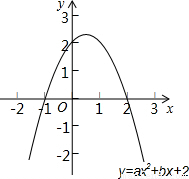


 (2012•大兴区二模)已知二次函数y=ax2+bx+2,它的图象经过点(1,2).
(2012•大兴区二模)已知二次函数y=ax2+bx+2,它的图象经过点(1,2).![]() ,其中O为坐标原点,试用含a的代数式表示k;
,其中O为坐标原点,试用含a的代数式表示k;![]() ,试确定a的取值范围.
,试确定a的取值范围.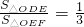 ,其中O为坐标原点,试用含a的代数式表示k;
,其中O为坐标原点,试用含a的代数式表示k; ≤m≤3
≤m≤3 ,试确定a的取值范围.
,试确定a的取值范围.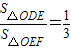 ,其中O为坐标原点,试用含a的代数式表示k;
,其中O为坐标原点,试用含a的代数式表示k; ≤m≤3
≤m≤3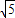 ,试确定a的取值范围.
,试确定a的取值范围.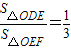 ,其中O为坐标原点,试用含a的代数式表示k;
,其中O为坐标原点,试用含a的代数式表示k;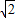 ≤m≤3
≤m≤3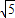 ,试确定a的取值范围.
,试确定a的取值范围.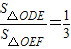 ,其中O为坐标原点,试用含a的代数式表示k;
,其中O为坐标原点,试用含a的代数式表示k;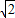 ≤m≤3
≤m≤3 ,试确定a的取值范围.
,试确定a的取值范围.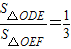 ,其中O为坐标原点,试用含a的代数式表示k;
,其中O为坐标原点,试用含a的代数式表示k;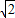 ≤m≤3
≤m≤3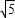 ,试确定a的取值范围.
,试确定a的取值范围. ,其中O为坐标原点,试用含a的代数式表示k;
,其中O为坐标原点,试用含a的代数式表示k; ≤m≤3
≤m≤3 ,试确定a的取值范围.
,试确定a的取值范围.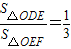 ,其中O为坐标原点,试用含a的代数式表示k;
,其中O为坐标原点,试用含a的代数式表示k; ≤m≤3
≤m≤3 ,试确定a的取值范围.
,试确定a的取值范围.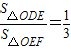 ,其中O为坐标原点,试用含a的代数式表示k;
,其中O为坐标原点,试用含a的代数式表示k; ≤m≤3
≤m≤3 ,试确定a的取值范围.
,试确定a的取值范围.