
已知二次函数y=ax2+bx+2,它的图象经过点(1,2).
(1)如果用含a的代数式表示b,那么b= ;
(2)如图所示,如果该图象与x轴的一个交点为(﹣1,0).

①求二次函数的表达式,并写出图象的顶点坐标;
②在平面直角坐标系中,如果点P到x轴与y轴的距离相等,则称点P为等距点.求出这个二次函数图象上所有等距点的坐标.
(3)当a取a1,a2时,二次函数图象与x轴正半轴分别交于点M(m,0),点N(n,0).如果点N在点M的右边,且点M和点N都在点(1,0)的右边.试比较a1和a2的大小.
(1)﹣a (2)①y=﹣x2+x+2,顶点坐标为;( ,
,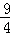 )②P1(
)②P1(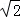 ,
,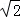 )、P2(
)、P2(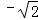 ,﹣
,﹣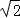 )、P3(1+
)、P3(1+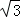 ,﹣1﹣
,﹣1﹣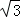 )、P4(1﹣
)、P4(1﹣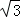 ,
,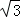 ﹣1)(3)a1<a2.
﹣1)(3)a1<a2.
【解析】
试题分析:(1)直接将点(1,2)代入抛物线的解析式中,即可得到a、b间的关系式.
(2)①已知抛物线图象上的两点坐标,且只有两个待定系数,利用待定系数法求解即可.
②P到x轴、y轴的距离相等,那么P点必在直线y=x或y=﹣x上,这两条直线与抛物线的交点,即为符合条件的等距点.
(3)首先根据(1)的结论,用a表示出函数的解析式,然后分别将M、N的坐标代入抛物线的解析式中,分别用m、n表示出a1、a2,通过做差可比较出a1、a2的大小.
试题解析:(1)将(1,2)代入y=ax2+bx+2中,得:
a+b+2=2,得:b=﹣a.
(2)①∵二次函数y=ax2+bx+c经过点(1,2)和(﹣1,0)
可得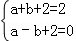 ,
,
解得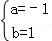 ,
,
即y=﹣x2+x+2,
顶点坐标为( ,
,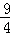 ).
).
②该函数图象上等距点的坐标即为此函数与函数y1=x和函数y2=﹣x的交点坐标
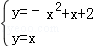 ,
,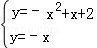 ,
,
解得P1(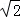 ,
,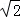 )、P2(
)、P2(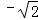 ,﹣
,﹣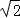 )、P3(1+
)、P3(1+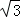 ,﹣1﹣
,﹣1﹣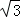 )、P4(1﹣
)、P4(1﹣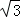 ,
,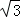 ﹣1).
﹣1).
(3)∵二次函数与x轴正半轴交于点(m,0)且a=﹣b,
∴a1m2﹣a1m+2=0,即 a1=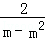 ,
,
同理 a2n2﹣a2n+2=0,a2=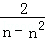 ,
,
故 a2﹣a1=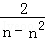 ﹣
﹣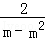 =
=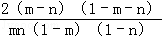 ,
,
∵n>m>1,故 a2﹣a1=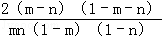 >0,
>0,
∴a1<a2.
考点:二次函数综合题.


科目:初中数学 来源:2013-2014学年浙江省宁波市九年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,点A在双曲线 上,点B在双曲线
上,点B在双曲线 上,且AB//
上,且AB// 轴,点P是
轴,点P是 轴上的任意一点,则△PAB的面积为 .
轴上的任意一点,则△PAB的面积为 .

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省九年级直升班第一次综合测试数学试卷(解析版) 题型:解答题
如图1,在⊙O中,E是弧AB的中点,C为⊙O上的一动点(C与E在AB异侧),连接EC交AB于点F,EB=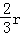 (r是⊙O的半径).
(r是⊙O的半径).
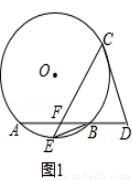
(1)D为AB延长线上一点,若DC=DF,证明:直线DC与⊙O相切;
(2)如图2,当F是AB的四等分点且EF·EC=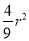 时,求EC的值.
时,求EC的值.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省九年级直升班第一次综合测试数学试卷(解析版) 题型:选择题
下列四个三角形中,与右图中的三角形相似的是( )


A. B. C. D.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省中考模拟数学试卷(解析版) 题型:解答题
如图,某同学在大楼AD的观光电梯中的E点测得大楼BC楼底C点的俯角为45°,此时该同学距地面高度AE为20米,电梯再上升5米到达D点,此时测得大楼BC楼顶B点的仰角为37°,求大楼的高度BC.

(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省中考模拟数学试卷(解析版) 题型:填空题
如图,△ABC绕点A顺时针旋转100°得到△AEF,若∠C=60°,∠E=100°,则α的度数为 .

查看答案和解析>>
科目:初中数学 来源:2013-2014学年新疆阿拉尔市九年级秋季班第一次月考数学试卷(解析版) 题型:解答题
阅读下面的例题:
解方程
【解析】
当x≥0时,原方程化为x2-x-2=0,解得:x1=2,x2=-1(不合题意,舍去);
当x<0时,原方程化为x2+ x-2=0,解得:x1=1,(不合题意,舍去)x2=-2;
∴原方程的根是x1=2,x2=-2.
请参照例题解方程 .
.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年广东省深圳市海怡翠学校九年级上学期期中考试数学试卷(解析版) 题型:选择题
如果小强将镖随意投中如图所示的正方形木板,那么镖落在阴影部分的概率为( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com