练习册

  • 练习册
  • 试题
    精英家教网 > 试题搜索列表 >关于x的一元二次方程x的平方-bx+c=0中

    关于x的一元二次方程x的平方-bx+c=0中答案解析

    科目：czsx 来源： 题型：

    关于x的一元二次方程x2-6x+k=0的一个根是2．
    （1）求k的值和方程的另一个根x2；
    （2）若直线AB经过点A（2，0），B（0，x2），求直线AB的解析式；
    （3）在平面直角坐标系中画出直线AB的图象，P是x轴上一动点，是否存在点P，使△ABP是直角三角形，若存在，求出点P坐标，若不存在，说明理由．

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

    关于x的一元二次方程x2-6x+k=0的一个根是2．
    （1）求k的值和方程的另一个根x2；
    （2）若直线AB经过点A（2，0），B（0，x2），求直线AB的解析式；
    （3）在平面直角坐标系中画出直线AB的图象，P是x轴上一动点，是否存在点P，使△ABP是直角三角形，若存在，求出点P坐标，若不存在，说明理由．

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

    关于x的一元二次方程x2-4x+c=0有实数根，且c为正整数．
    （1）求c的值；
    （2）若此方程的两根均为整数，在平面直角坐标系xOy中，抛物线y=x2-4x+c与x轴交于A、B两点（A在B左侧），与y轴交于点C．点P为对称轴上一点，且四边形OBPC为直角梯形，求PC的长；
    （3）将（2）中得到的抛物线沿水平方向平移，设顶点D的坐标为（m，n），当抛物线与（2）中的直角梯形OBPC只有两个交点，且一个交点在PC边上时，直接写出m的取值范围．

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

    关于x的一元二次方程x2-4x+k+2=0有两个实数根，且k为正整数．
    （1）求k的值；
    （2）当此方程有两个不相等的实数根时，将关于x的二次函数y=x2-4x+k+2的图象向下平移3个单位，求平移后图象的解析式，并在所给的直角坐标系中描点画出它的图象．

    查看答案和解析>>

    科目：czsx 来源：北京模拟题 题型：解答题

    关于x的一元二次方程x2-4x+c=0有实数根，且c为正整数。
    （1）求c的值；
    （2）若此方程的两根均为整数，在平面直角坐标系xOy中，抛物线y=x2-4x+c与x轴交于A、B两点（A在B左侧），与y轴交于点C，点P为对称轴上一点，且四边形OBPC为直角梯形，求PC的长；
    （3）将（2）中得到的抛物线沿水平方向平移，设顶点D的坐标为（m，n），当抛物线与（2）中的直角梯形OBPC只有两个交点，且一个交点在PC边上时，直接写出m的取值范围。

    查看答案和解析>>

    科目：czsx 来源：2011-2012学年福建省福州市台江区九年级（上）期中数学试卷（解析版） 题型：解答题

    关于x的一元二次方程x2-6x+k=0的一个根是2．
    （1）求k的值和方程的另一个根x2；
    （2）若直线AB经过点A（2，0），B（0，x2），求直线AB的解析式；
    （3）在平面直角坐标系中画出直线AB的图象，P是x轴上一动点，是否存在点P，使△ABP是直角三角形，若存在，求出点P坐标，若不存在，说明理由．

    查看答案和解析>>

    科目：czsx 来源：2011年江苏省南通市崇川区中考数学模拟试卷（解析版） 题型：解答题

    关于x的一元二次方程x2-4x+k+2=0有两个实数根，且k为正整数．
    （1）求k的值；
    （2）当此方程有两个不相等的实数根时，将关于x的二次函数y=x2-4x+k+2的图象向下平移3个单位，求平移后图象的解析式，并在所给的直角坐标系中描点画出它的图象．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    对于每个正整数n，关于x的一元二次方程x2-
    2n+1
    n(n+1)
    x+
    1
    n(n+1)
    =0    的两个根分别为an、bn，设平面直角坐标系中，An、Bn两点的坐标分别为An（an，0），Bn（bn，0），AnBn表示这两点间的距离，则AnBn=
    1
    n(n+1)
    1
    n(n+1)
    （用含n的代数式表示）；A1B1+A2B2+…+A2012B2012的值为
    2011
    2012
    2011
    2012
    ．

    查看答案和解析>>

    科目：czsx 来源： 题型：填空题

    对于每个正整数n，关于x的一元二次方程数学公式的两个根分别为an、bn，设平面直角坐标系中，An、Bn两点的坐标分别为An（an，0），Bn（bn，0），AnBn表示这两点间的距离，则AnBn=________（用含n的代数式表示）；A1B1+A2B2+…+A2012B2012的值为________．

    查看答案和解析>>

    科目：czsx 来源：不详 题型：填空题

    对于每个正整数n，关于x的一元二次方程x2-
    2n+1
    n(n+1)
    x+
    1
    n(n+1)
    =0    的两个根分别为an、bn，设平面直角坐标系中，An、Bn两点的坐标分别为An（an，0），Bn（bn，0），AnBn表示这两点间的距离，则AnBn=______（用含n的代数式表示）；A1B1+A2B2+…+A2012B2012的值为______．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    23、关于x的一元二次方程x2-4x+c=0有实数根，且c为正整数．
    （1）求c的值；
    （2）若此方程的两根均为整数，在平面直角坐标系xOy中，抛物线y=x2-4x+c与x轴交于A、B两点（A在B左侧），与y轴交于点C．点P为对称轴上一点，且四边形OBPC为直角梯形，求PC的长；
    （3）将（2）中得到的抛物线沿水平方向平移，设顶点D的坐标为（m，n），当抛物线与（2）中的直角梯形OBPC只有两个交点，且一个交点在PC边上时，直接写出m的取值范围．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知关于x的一元二次方程kx2+（3k+1）x+2k+1=0．
    （1）求证：该方程必有两个实数根；
    （2）若该方程只有整数根，求k的整数值；
    （3）在（2）的条件下，在平面直角坐标系中，若二次函数y=（k+1）x2+3x+m与x轴有两个不同的交点A和B（A在B左侧），并且满足OA=2•OB，求m的非负整数值．

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

    已知关于x的一元二次方程x2+（4-m）x+1-m=0．
    （1）求证：无论m取何值，此方程总有两个不相等的实数根；
    （2）此方程有一个根是-3，在平面直角坐标系xOy中，将抛物线y=x2+（4-m）x+1-m向右平移3个单位，得到一个新的抛物线，当直线y=x+b与这个新抛物线有且只有一个公共点时，求b的值．

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

    已知关于x的一元二次方程2x2+（a+4）x+a=0．
    （1）求证：无论a为任何实数，此方程总有两个不相等的实数根；
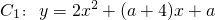    （2）抛物线数学公式与x轴的一个交点的横坐标为数学公式，其中a≠0，将抛物线C1向右平移数学公式个单位，再向上平移数学公式个单位，得到抛物线C2．求抛物线C2的解析式；
    （3）点A（m，n）和B（n，m）都在（2）中抛物线C2上，且A、B两点不重合，求代数式2m3-2mn+2n3的值．

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

    已知关于x的一元二次方程x2-mx+2m-1=0的两个实数根的平方和为23，求m的值．
    某同学的解答如下：
    解：设x1、x2是方程的两根，
    由根与系数的关系，得x1+x2=-m，x1x2=2m-1；
    由题意，得x12+x22=23；
    又x12+x22=（x1+x2）2-2x1x2；
    ∴m2-2（2m-1）=23．
    解之，得m1=7，m2=-3，
    所以，m的值为7或-3．
    上述解答中有错误，请你指出错误之处，并重新给出完整的解答．

    查看答案和解析>>

    科目：czsx 来源： 题型：解答题

    已知关于x的一元二次方程kx2+（3k+1）x+2k+1=0．
    （1）求证：该方程必有两个实数根；
    （2）若该方程只有整数根，求k的整数值；
    （3）在（2）的条件下，在平面直角坐标系中，若二次函数y=（k+1）x2+3x+m与x轴有两个不同的交点A和B（A在B左侧），并且满足OA=2•OB，求m的非负整数值．

    查看答案和解析>>

    科目：czsx 来源：淮安 题型：解答题

    已知关于x的一元二次方程x2-mx+2m-1=0的两个实数根的平方和为23，求m的值．
    某同学的解答如下：
    设x1、x2是方程的两根，
    由根与系数的关系，得x1+x2=-m，x1x2=2m-1；
    由题意，得x12+x22=23；
    又x12+x22=（x1+x2）2-2x1x2；
    ∴m2-2（2m-1）=23．
    解之，得m1=7，m2=-3，
    所以，m的值为7或-3．
    上述解答中有错误，请你指出错误之处，并重新给出完整的解答．

    查看答案和解析>>

    科目：czsx 来源：不详 题型：解答题

    已知关于x的一元二次方程kx2+（3k+1）x+2k+1=0．
    （1）求证：该方程必有两个实数根；
    （2）若该方程只有整数根，求k的整数值；
    （3）在（2）的条件下，在平面直角坐标系中，若二次函数y=（k+1）x2+3x+m与x轴有两个不同的交点A和B（A在B左侧），并且满足OA=2•OB，求m的非负整数值．

    查看答案和解析>>

    科目：czsx 来源： 题型：

    已知关于x的一元二次方程kx2＋（3k＋1）x＋2k＋1＝0.

    （1）求证：该方程必有两个实数根.

    （2）若该方程只有整数根，求k的整数值

    （3）在（2）的条件下，在平面直角坐标系中，若二次函数y＝（k＋1）x2＋3x＋m与x轴有两个不同的交点A和B（A在B左侧），并且满足OA=2·OB，求m的非负整数值.

    查看答案和解析>>

    科目：czsx 来源：2009-2010学年九年级（上）期末数学复习测试卷（B）（解析版） 题型：解答题

    已知关于x的一元二次方程x2-mx+2m-1=0的两个实数根的平方和为23，求m的值．
    某同学的解答如下：
    解：设x1、x2是方程的两根，
    由根与系数的关系，得x1+x2=-m，x1x2=2m-1；
    由题意，得x12+x22=23；
    又x12+x22=（x1+x2）2-2x1x2；
    ∴m2-2（2m-1）=23．
    解之，得m1=7，m2=-3，
    所以，m的值为7或-3．
    上述解答中有错误，请你指出错误之处，并重新给出完整的解答．

    查看答案和解析>>