
科目:czsx 来源: 题型:
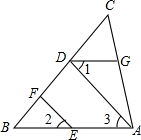 如图EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.
如图EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.科目:czsx 来源: 题型:解答题
 如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.
如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.科目:czsx 来源: 题型:解答题
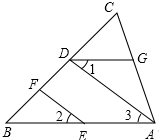 如图,EF⊥BC,AD⊥BC,∠1=∠2,∠BAC=80°.求∠AGD的度数.
如图,EF⊥BC,AD⊥BC,∠1=∠2,∠BAC=80°.求∠AGD的度数.科目:czsx 来源: 题型:
 补全下列推理过程:
补全下列推理过程:科目:czsx 来源: 题型:
 如图,已知点D、F、E、G都在△ABC的边上,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.(请在下面的空格处填写理由或数学式)
如图,已知点D、F、E、G都在△ABC的边上,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.(请在下面的空格处填写理由或数学式)科目:czsx 来源: 题型:填空题
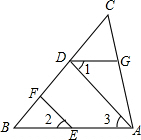 如图,已知点D、F、E、G都在△ABC的边上,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.(请在下面的空格处填写理由或数学式)
如图,已知点D、F、E、G都在△ABC的边上,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.(请在下面的空格处填写理由或数学式)科目:czsx 来源: 题型:
 26、完成下面的解题过程,并在括号内填上依据.如图,EF∥AD,∠1=∠2,∠BAC=85°.求∠AGD的度数.
26、完成下面的解题过程,并在括号内填上依据.如图,EF∥AD,∠1=∠2,∠BAC=85°.求∠AGD的度数.科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
 现有两块大小相同的直角三角板△ABC、△DEF,∠ACB=∠DFE=90°,∠A=∠D=30°.将这两块三角板摆成如图a的形式,使B、F、E、A在同一条直线上,点C在边DF上,DE与AC相交于点G,求∠AGD的度数.
现有两块大小相同的直角三角板△ABC、△DEF,∠ACB=∠DFE=90°,∠A=∠D=30°.将这两块三角板摆成如图a的形式,使B、F、E、A在同一条直线上,点C在边DF上,DE与AC相交于点G,求∠AGD的度数.科目:czsx 来源: 题型:解答题
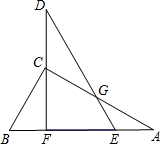 现有两块大小相同的直角三角板△ABC、△DEF,∠ACB=∠DFE=90°,∠A=∠D=30°.将这两块三角板摆成如图a的形式,使B、F、E、A在同一条直线上,点C在边DF上,DE与AC相交于点G,求∠AGD的度数.
现有两块大小相同的直角三角板△ABC、△DEF,∠ACB=∠DFE=90°,∠A=∠D=30°.将这两块三角板摆成如图a的形式,使B、F、E、A在同一条直线上,点C在边DF上,DE与AC相交于点G,求∠AGD的度数.科目:czsx 来源: 题型:
现有两块大小相同的直角三角板△ABC、△DEF,∠ACB=∠DFE=90°,
∠A=∠D=30°.

(1)将这两块三角板摆成如图①的形式,使B、F、E、A在同一条直线上,点C在边DF上,DE与AC相交于点G,试求∠AGD的度数;
(2)将图①中的△ABC固定,把△DEF绕着点F逆时针旋转成如图②的形式,当旋转的角度等于多少度时,DF∥AC? 并说明理由.
科目:czsx 来源: 题型:

科目:czsx 来源:2010-2011学年江苏南京市第三初级中学七年级下学期期中考试数学卷(带解析) 题型:解答题
现有两块大小相同的直角三角板△ABC、△DEF,∠ACB=∠DFE=90°,
∠A=∠D=30°.
(1)将这两块三角板摆成如图①的形式,使B、F、E、A在同一条直线上,点C在边DF上,DE与AC相交于点G,试求∠AGD的度数;
(2)将图①中的△ABC固定,把△DEF绕着点F逆时针旋转成如图②的形式,当旋转的角度等于多少度时,DF∥AC? 并说明理由.
科目:czsx 来源:2013届江苏南京市七年级下学期期中考试数学卷(解析版) 题型:解答题
现有两块大小相同的直角三角板△ABC、△DEF,∠ACB=∠DFE=90°,
∠A=∠D=30°.

(1)将这两块三角板摆成如图①的形式,使B、F、E、A在同一条直线上,点C在边DF上,DE与AC相交于点G,试求∠AGD的度数;
(2)将图①中的△ABC固定,把△DEF绕着点F逆时针旋转成如图②的形式,当旋转的角度等于多少度时,DF∥AC? 并说明理由.
科目:czsx 来源: 题型:解答题

科目:czsx 来源:期中题 题型:证明题

科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
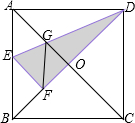 如图,在正方形纸片ABCD中,对角线AC,BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB,AC于点G,E,连接GF.
如图,在正方形纸片ABCD中,对角线AC,BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB,AC于点G,E,连接GF.