
科目:czsx 来源: 题型:
科目:czsx 来源:2011-2012学年江苏省锡中实验学校八年级下学期期中考试数学卷(带解析) 题型:解答题
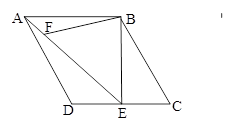
如图,在菱形ABCD中,∠C=60°,AB=4,过点B作BE⊥CD,垂足为E,连结AE.F为AE上一点,且∠BFE=60°. 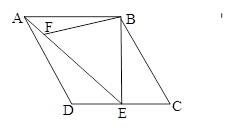
(1)求证:△ABF∽△EAD;
(2)求BF的长.
科目:czsx 来源: 题型:
如图,在菱形ABCD中,∠C=60°,AB=4,过点B作BE⊥CD,垂足为E,连结AE.F为AE上一点,且∠BFE=60°.
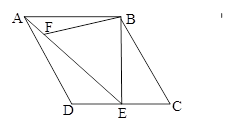
(1)求证:△ABF∽△EAD;
(2)求BF的长.
【解析】根据菱形的性质及相似三角形的判定方法得到△ABF∽△EAD,再根据相似三角形的边对应成比例即可求得BF的长
科目:czsx 来源:2013届江苏省锡中实验学校八年级下学期期中考试数学卷(解析版) 题型:解答题
如图,在菱形ABCD中,∠C=60°,AB=4,过点B作BE⊥CD,垂足为E,连结AE.F为AE上一点,且∠BFE=60°.

(1)求证:△ABF∽△EAD;
(2)求BF的长.
【解析】根据菱形的性质及相似三角形的判定方法得到△ABF∽△EAD,再根据相似三角形的边对应成比例即可求得BF的长
科目:czsx 来源:不详 题型:解答题

科目:czsx 来源:1+1轻巧夺冠·优化训练·八年级数学下 题型:013
如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,联结DF,则∠CDF等于
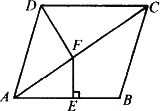
A.60°
B.65°
C.70°
D.80°
科目:czsx 来源:精编教材全解 数学 八年级上册 配苏科版 配苏科版 题型:013
如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于
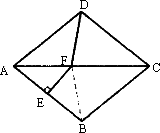
A.80°
B.70°
C.65°
D.60°
科目:czsx 来源:新课程同步练习 数学 八年级下册 人教版 题型:013
如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于

A.80°
B.70°
C.65°
D.60°
科目:czsx 来源:学习周报 数学 北师大八年级版 2009-2010学年 第9期 总第165期 北大师版 题型:013
如图,在菱形
ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于
A.80°
B.70°
C.65°
D.60°
科目:czsx 来源:非常讲解·教材全解全析 数学 九年级下 (配北师大课标) 配北师大课标 题型:013
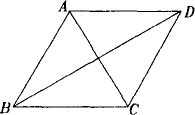
如图,在菱形ABCD中,∠ABC=60°,AC=4,则BD的长为
A.8![]()
B.4![]()
C.2![]()
D.8
科目:czsx 来源:101网校同步练习 初三数学 北师大(新课标2001/3年初审) 北师大版 题型:044
如图,在菱形ABCD中,AB=CD=10,∠BAD=60°,点M从点A以每秒1个单位长的速度沿着AD边向点D移动;设点M移动的时间为t秒(0≤t≤10),

(1)点N为BC边上任意一点,在点M移动过程中的某一时刻,线段MN是否可以将菱形ABCD分割成面积相等的两部分?并说明理由;
(2)点N从点B(与点M出发的时刻相同)以每秒2个单位长的速度沿着BC边向点C移动,在什么时候梯形ABNM的面积最大?并求出面积的最大值;
(3)点N从点B(与点M出发的时刻相同)以每秒a(a≥2)个单位长的速度沿着射线BC方向(可以超越点C)移动,过点M作MP∥AB,交BC于点P,当△MPN≌△ABC时,设△MPN与菱形ABCD重叠部分的面积为S,求出用t表示S的关系式,并求当S=0时a的值.
科目:czsx 来源:2013年江苏省扬州市高级中等学校招生考试数学 题型:013
如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于
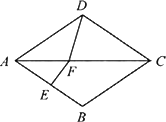
A.50°
B.60°
C.70°
D.80°
科目:czsx 来源:2007年德州市初中毕业、升学统一考试数学试卷 题型:022
如图,在菱形ABCD中,∠B=60°,点E,F分别从点B,D出发以同样的速度沿边BC,DC向点C运动.给出以下四个结论:①AE=AF②∠CEF=∠CFE③当点E,F分别为边BC,DC的中点时,△AEF是等边三角形④当点E,F分别为边BC,DC的中点时,△AEF的面积最大.上述结论中正确的序号有________.(把你认为正确的序号都填上)

科目:czsx 来源:2013年浙江省衢州市高级中等学校招生考试数学 题型:022
如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去…….则四边形A2B2C2D2的周长是________;四边形A2013B2013C2013D2013的周长是________.
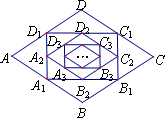
科目:czsx 来源:河南省2012年中考数学试题 题型:044
如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.

(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为________时,四边形AMDN是矩形;
②当AM的值为________时,四边形AMDN是菱形.
科目:czsx 来源:2013年广西省南宁市高级中等学校招生考试数学 题型:044
如图,在菱形ABCD中,AC是对角线,点E、F分别是边BC、AD的中点.

(1)求证:△ABE≌△CDF.
(2)若∠B=60°,AB=4,求线段AE的长.
科目:czsx 来源:2009年贵州省贵阳中考数学试题及答案 题型:044
如图,在菱形ABCD中,P是AB上的一个动点(不与A、B重合).连接OP交对角线AC于E连接BE.
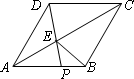
(1)证明:∠APD=∠CBE;
(2)若∠DAB=60°,试问P点运动到什么位置时,△ADP的面积等于菱形ABCD面积的![]() ?为什么?
?为什么?
科目:czsx 来源:新人教版(2012) 八年级下 题型:
| |||||||||||||||
科目:czsx 来源:新人教版(2012) 八年级下 题型:
| |||||||||||||||
科目:czsx 来源: 题型:
如图,在菱形ABCD中,P是AB上的一个动点(不与A、B重合)。连接DP交对角线AC于E,连接BE。
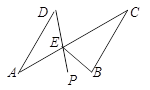
(1) 证明:∠APD=∠CBE;
(2) 若∠DAB=60º,试问P点运动到什么位置时,△ADP的面积等于菱形ABCD面积的?
请说明理由。