如图.抛物线y=ax^2+bx+c的图象经过点A答案解析
科目:czsx
来源:
题型:
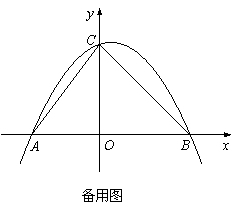
如图,已知抛物线y=ax+bx-4经过点A(-2,0),B(4,O)与y轴交于C点.
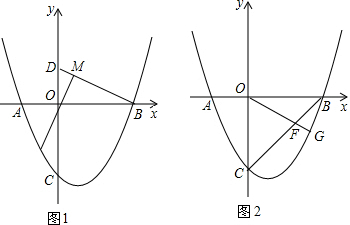
(1)求抛物线的解析式.
(2)若D点坐标为(0,2),P为抛物线第三象限上一动点,连PO交BD于M点,问是否存在一点P,使
=
?若存在,求P点坐标;不存在,请说明理由.
(3)G为抛物线第四象限上一点,OG交BC于F,求当GF:OF的比值最大时G点的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
如图,已知抛物线y=ax+bx-4经过点A(-2,0),B(4,O)与y轴交于C点.
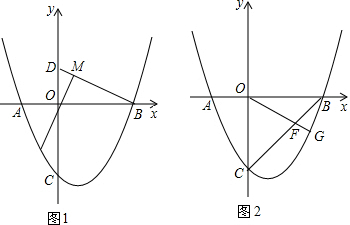
(1)求抛物线的解析式.
(2)若D点坐标为(0,2),P为抛物线第三象限上一动点,连PO交BD于M点,问是否存在一点P,使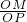 =
= ?若存在,求P点坐标;不存在,请说明理由.
?若存在,求P点坐标;不存在,请说明理由.
(3)G为抛物线第四象限上一点,OG交BC于F,求当GF:OF的比值最大时G点的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:
已知:抛物线y=ax
2+bx+c(a≠0)的图象经过点(1,0),一条直线y=ax+b,它们的系数之间满足如下关系:a>b>c.
(1)求证:抛物线与直线一定有两个不同的交点;
(2)设抛物线与直线的两个交点为A、B,过A、B分别作x轴的垂线,垂足分别为A
1、B
1.令
k=,试问:是否存在实数k,使线段A
1B
1的长为
4.如果存在,求出k的值;如果不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
已知:抛物线y=ax2+bx+c(a≠0)的图象经过点(1,0),一条直线y=ax+b,它们的系数之间满足如下关系:a>b>c.
(1)求证:抛物线与直线一定有两个不同的交点;
(2)设抛物线与直线的两个交点为A、B,过A、B分别作x轴的垂线,垂足分别为A1、B1.令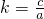 ,试问:是否存在实数k,使线段A1B1的长为
,试问:是否存在实数k,使线段A1B1的长为 .如果存在,求出k的值;如果不存在,请说明理由.
.如果存在,求出k的值;如果不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(45):2.7 最大面积是多少(解析版)
题型:解答题
已知:抛物线y=ax
2+bx+c(a≠0)的图象经过点(1,0),一条直线y=ax+b,它们的系数之间满足如下关系:a>b>c.
(1)求证:抛物线与直线一定有两个不同的交点;
(2)设抛物线与直线的两个交点为A、B,过A、B分别作x轴的垂线,垂足分别为A
1、B
1.令
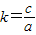
,试问:是否存在实数k,使线段A
1B
1的长为
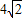
.如果存在,求出k的值;如果不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:第34章《二次函数》中考题集(49):34.4 二次函数的应用(解析版)
题型:解答题
已知:抛物线y=ax
2+bx+c(a≠0)的图象经过点(1,0),一条直线y=ax+b,它们的系数之间满足如下关系:a>b>c.
(1)求证:抛物线与直线一定有两个不同的交点;
(2)设抛物线与直线的两个交点为A、B,过A、B分别作x轴的垂线,垂足分别为A
1、B
1.令

,试问:是否存在实数k,使线段A
1B
1的长为

.如果存在,求出k的值;如果不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(48):2.3 二次函数的应用(解析版)
题型:解答题
已知:抛物线y=ax
2+bx+c(a≠0)的图象经过点(1,0),一条直线y=ax+b,它们的系数之间满足如下关系:a>b>c.
(1)求证:抛物线与直线一定有两个不同的交点;
(2)设抛物线与直线的两个交点为A、B,过A、B分别作x轴的垂线,垂足分别为A
1、B
1.令

,试问:是否存在实数k,使线段A
1B
1的长为

.如果存在,求出k的值;如果不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:第27章《二次函数》中考题集(48):27.3 实践与探索(解析版)
题型:解答题
已知:抛物线y=ax
2+bx+c(a≠0)的图象经过点(1,0),一条直线y=ax+b,它们的系数之间满足如下关系:a>b>c.
(1)求证:抛物线与直线一定有两个不同的交点;
(2)设抛物线与直线的两个交点为A、B,过A、B分别作x轴的垂线,垂足分别为A
1、B
1.令
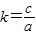
,试问:是否存在实数k,使线段A
1B
1的长为

.如果存在,求出k的值;如果不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:第26章《二次函数》中考题集(46):26.3 实际问题与二次函数(解析版)
题型:解答题
已知:抛物线y=ax
2+bx+c(a≠0)的图象经过点(1,0),一条直线y=ax+b,它们的系数之间满足如下关系:a>b>c.
(1)求证:抛物线与直线一定有两个不同的交点;
(2)设抛物线与直线的两个交点为A、B,过A、B分别作x轴的垂线,垂足分别为A
1、B
1.令

,试问:是否存在实数k,使线段A
1B
1的长为

.如果存在,求出k的值;如果不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(50):2.8 二次函数的应用(解析版)
题型:解答题
已知:抛物线y=ax
2+bx+c(a≠0)的图象经过点(1,0),一条直线y=ax+b,它们的系数之间满足如下关系:a>b>c.
(1)求证:抛物线与直线一定有两个不同的交点;
(2)设抛物线与直线的两个交点为A、B,过A、B分别作x轴的垂线,垂足分别为A
1、B
1.令

,试问:是否存在实数k,使线段A
1B
1的长为

.如果存在,求出k的值;如果不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:第20章《二次函数和反比例函数》中考题集(45):20.5 二次函数的一些应用(解析版)
题型:解答题
已知:抛物线y=ax
2+bx+c(a≠0)的图象经过点(1,0),一条直线y=ax+b,它们的系数之间满足如下关系:a>b>c.
(1)求证:抛物线与直线一定有两个不同的交点;
(2)设抛物线与直线的两个交点为A、B,过A、B分别作x轴的垂线,垂足分别为A
1、B
1.令
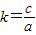
,试问:是否存在实数k,使线段A
1B
1的长为

.如果存在,求出k的值;如果不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:第2章《二次函数》中考题集(45):2.4 二次函数的应用(解析版)
题型:解答题
已知:抛物线y=ax
2+bx+c(a≠0)的图象经过点(1,0),一条直线y=ax+b,它们的系数之间满足如下关系:a>b>c.
(1)求证:抛物线与直线一定有两个不同的交点;
(2)设抛物线与直线的两个交点为A、B,过A、B分别作x轴的垂线,垂足分别为A
1、B
1.令

,试问:是否存在实数k,使线段A
1B
1的长为

.如果存在,求出k的值;如果不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:第23章《二次函数与反比例函数》中考题集(45):23.5 二次函数的应用(解析版)
题型:解答题
已知:抛物线y=ax
2+bx+c(a≠0)的图象经过点(1,0),一条直线y=ax+b,它们的系数之间满足如下关系:a>b>c.
(1)求证:抛物线与直线一定有两个不同的交点;
(2)设抛物线与直线的两个交点为A、B,过A、B分别作x轴的垂线,垂足分别为A
1、B
1.令

,试问:是否存在实数k,使线段A
1B
1的长为

.如果存在,求出k的值;如果不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:2005年全国中考数学试题汇编《二次函数》(06)(解析版)
题型:解答题
(2005•扬州)已知:抛物线y=ax
2+bx+c(a≠0)的图象经过点(1,0),一条直线y=ax+b,它们的系数之间满足如下关系:a>b>c.
(1)求证:抛物线与直线一定有两个不同的交点;
(2)设抛物线与直线的两个交点为A、B,过A、B分别作x轴的垂线,垂足分别为A
1、B
1.令

,试问:是否存在实数k,使线段A
1B
1的长为

.如果存在,求出k的值;如果不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:2005年江苏省扬州市中考数学试卷(大纲卷)(解析版)
题型:解答题
(2005•扬州)已知:抛物线y=ax
2+bx+c(a≠0)的图象经过点(1,0),一条直线y=ax+b,它们的系数之间满足如下关系:a>b>c.
(1)求证:抛物线与直线一定有两个不同的交点;
(2)设抛物线与直线的两个交点为A、B,过A、B分别作x轴的垂线,垂足分别为A
1、B
1.令
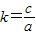
,试问:是否存在实数k,使线段A
1B
1的长为
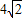
.如果存在,求出k的值;如果不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:2012年湖南省郴州市中考数学试卷(解析版)
题型:解答题
阅读下列材料:
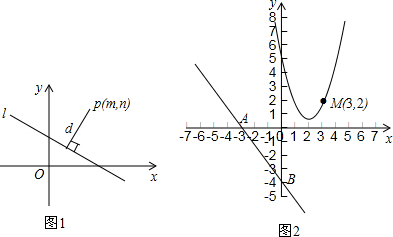
我们知道,一次函数y=kx+b的图象是一条直线,而y=kx+b经过恒等变形可化为直线的另一种表达形式:Ax+Bx+C=0(A、B、C是常数,且A、B不同时为0).如图1,点P(m,n)到直线l:Ax+By+C=0的距离(d)计算公式是:d=
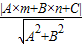
.
例:求点P(1,2)到直线y=
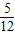
x-

的距离d时,先将y=

化为5x-12y-2=0,再由上述距离公式求得d=

=

.
解答下列问题:
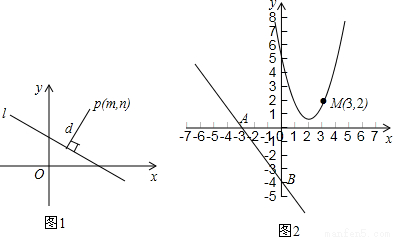
如图2,已知直线y=-
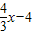
与x轴交于点A,与y轴交于点B,抛物线y=x
2-4x+5上的一点M(3,2).
(1)求点M到直线AB的距离.
(2)抛物线上是否存在点P,使得△PAB的面积最小?若存在,求出点P的坐标及△PAB面积的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:湖南省中考真题
题型:解答题
阅读下列材料: 我们知道,一次函数y=kx+b的图象是一条直线,而y=kx+b经过恒等变形可化为直线的另一种表达形式:Ax+Bx+C=0(A、B、C是常数,且A、B不同时为0).如图1,点P(m,n)到直线l:Ax+By+C=0的距离(d)计算公式是:d=
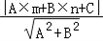
.
例:求点P(1,2)到直线y=
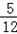
x﹣

的距离d时,先将y=
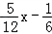
化为5x﹣12y﹣2=0,再由上述距离公式求得d=
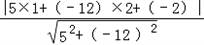
=
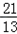
.
解答下列问题:
如图2,已知直线y=﹣
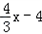
与x轴交于点A,与y轴交于点B,
抛物线y=x
2﹣4x+5上的一点M(3,2).
(1)求点M到直线AB的距离.
(2)抛物线上是否存在点P,使得△PAB的面积最小?若存在,求出点P的坐标及△PAB面积的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
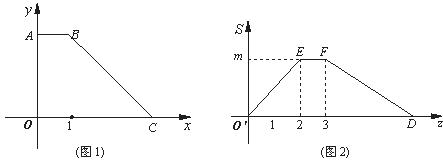
如图1,已知四边形OABC中的三个顶点坐标为O(0,0),A(0,n),C(m,0).动点P从点O出发依次沿线段OA,AB,BC向点C移动,设移动路程为z,△OPC的面积S随着z的变化而变化的图象如图2所示.m,n是常数, m>1,n>0.
(1)请你确定n的值和点B的坐标;
(2)当动点P是经过点O,C的抛物线y=ax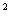 +bx+c的顶点,且在双曲线y=
+bx+c的顶点,且在双曲线y=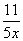 上时,求这时四边形OABC的面积.
上时,求这时四边形OABC的面积.
查看答案和解析>>
科目:czsx
来源:
题型:
如图,在平面直角坐标系中,抛物线y=ax 2+bx+4经过A(-3,0)、B(4,0)两点,且与y轴交于点C,D( ,0).动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时动点Q从点C出发,沿线段CA以某一速度向点A移动.
,0).动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时动点Q从点C出发,沿线段CA以某一速度向点A移动.
(1)求该抛物线的解析式;
(2)若经过t秒的 移动,线段PQ被CD垂直平分,求此时t的值;
移动,线段PQ被CD垂直平分,求此时t的值;
(3)在第一象限的抛物线上取一点G,使得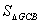 =
= ,再在抛物线上找点E(不与点A、B、C重合),使得∠GBE=45°,求E点的坐标.
,再在抛物线上找点E(不与点A、B、C重合),使得∠GBE=45°,求E点的坐标.

查看答案和解析>>



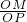 =
= ?若存在,求P点坐标;不存在,请说明理由.
?若存在,求P点坐标;不存在,请说明理由.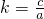 ,试问:是否存在实数k,使线段A1B1的长为
,试问:是否存在实数k,使线段A1B1的长为 .如果存在,求出k的值;如果不存在,请说明理由.
.如果存在,求出k的值;如果不存在,请说明理由.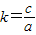 ,试问:是否存在实数k,使线段A1B1的长为
,试问:是否存在实数k,使线段A1B1的长为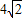 .如果存在,求出k的值;如果不存在,请说明理由.
.如果存在,求出k的值;如果不存在,请说明理由. ,试问:是否存在实数k,使线段A1B1的长为
,试问:是否存在实数k,使线段A1B1的长为 .如果存在,求出k的值;如果不存在,请说明理由.
.如果存在,求出k的值;如果不存在,请说明理由. ,试问:是否存在实数k,使线段A1B1的长为
,试问:是否存在实数k,使线段A1B1的长为 .如果存在,求出k的值;如果不存在,请说明理由.
.如果存在,求出k的值;如果不存在,请说明理由.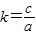 ,试问:是否存在实数k,使线段A1B1的长为
,试问:是否存在实数k,使线段A1B1的长为 .如果存在,求出k的值;如果不存在,请说明理由.
.如果存在,求出k的值;如果不存在,请说明理由. ,试问:是否存在实数k,使线段A1B1的长为
,试问:是否存在实数k,使线段A1B1的长为 .如果存在,求出k的值;如果不存在,请说明理由.
.如果存在,求出k的值;如果不存在,请说明理由. ,试问:是否存在实数k,使线段A1B1的长为
,试问:是否存在实数k,使线段A1B1的长为 .如果存在,求出k的值;如果不存在,请说明理由.
.如果存在,求出k的值;如果不存在,请说明理由.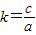 ,试问:是否存在实数k,使线段A1B1的长为
,试问:是否存在实数k,使线段A1B1的长为 .如果存在,求出k的值;如果不存在,请说明理由.
.如果存在,求出k的值;如果不存在,请说明理由. ,试问:是否存在实数k,使线段A1B1的长为
,试问:是否存在实数k,使线段A1B1的长为 .如果存在,求出k的值;如果不存在,请说明理由.
.如果存在,求出k的值;如果不存在,请说明理由. ,试问:是否存在实数k,使线段A1B1的长为
,试问:是否存在实数k,使线段A1B1的长为 .如果存在,求出k的值;如果不存在,请说明理由.
.如果存在,求出k的值;如果不存在,请说明理由. ,试问:是否存在实数k,使线段A1B1的长为
,试问:是否存在实数k,使线段A1B1的长为 .如果存在,求出k的值;如果不存在,请说明理由.
.如果存在,求出k的值;如果不存在,请说明理由.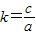 ,试问:是否存在实数k,使线段A1B1的长为
,试问:是否存在实数k,使线段A1B1的长为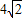 .如果存在,求出k的值;如果不存在,请说明理由.
.如果存在,求出k的值;如果不存在,请说明理由.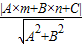 .
.
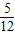 x-
x- 的距离d时,先将y=
的距离d时,先将y= 化为5x-12y-2=0,再由上述距离公式求得d=
化为5x-12y-2=0,再由上述距离公式求得d= =
= .
.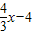 与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).
与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).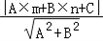 .
. 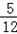 x﹣
x﹣ 的距离d时,先将y=
的距离d时,先将y=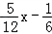 化为5x﹣12y﹣2=0,再由上述距离公式求得d=
化为5x﹣12y﹣2=0,再由上述距离公式求得d=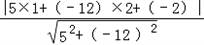 =
=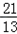 .
. 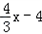 与x轴交于点A,与y轴交于点B,
与x轴交于点A,与y轴交于点B,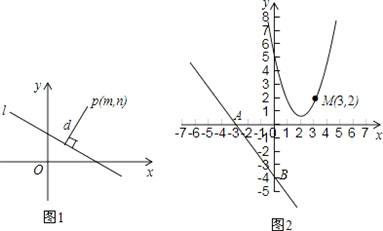
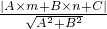 .
.
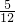 x-
x- 的距离d时,先将y=
的距离d时,先将y=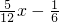 化为5x-12y-2=0,再由上述距离公式求得d=
化为5x-12y-2=0,再由上述距离公式求得d=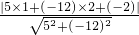 =
=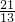 .
.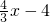 与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).
与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).![]() +bx+c的顶点,且在双曲线y=
+bx+c的顶点,且在双曲线y=![]() 上时,求这时四边形OABC的面积.
上时,求这时四边形OABC的面积.
 ,0).动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时动点Q从点C出发,沿线段CA以某一速度向点A移动.
,0).动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时动点Q从点C出发,沿线段CA以某一速度向点A移动. 移动,线段PQ被CD垂直平分,求此时t的值;
移动,线段PQ被CD垂直平分,求此时t的值;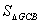 =
= ,再在抛物线上找点E(不与点A、B、C重合),使得∠GBE=45°,求E点的坐标.
,再在抛物线上找点E(不与点A、B、C重合),使得∠GBE=45°,求E点的坐标.
