
科目:czsx 来源: 题型:解答题
科目:czsx 来源: 题型:
科目:czsx 来源:2015-2016学年江苏省苏州市七年级上学期期中考试数学试卷(解析版) 题型:解答题
(12分)先化简,再求值:
(1) ,其中:
,其中: ,
,  .
.
(2)已知 ,且
,且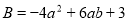 .
.
①求A等于多少;②若 ,求A的值.
,求A的值.
(3)已知多项式 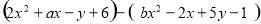 .
.
①若多项式的值与字母 的取值无关,求
的取值无关,求 、
、 的值;
的值;
②在①的条件下,先化简多项式 ,再求它的值.
,再求它的值.
科目:czsx 来源:江苏省期中题 题型:解答题
科目:czsx 来源: 题型:
为了推进节能减排,发展低碳经济,温州市某公司以 25万元购得某项节能产品的生产技术后,再投入100万元购买生产设备,进行该产品的生产加工,已知生产这种产品的成本价为每件20元,经过市场调研发现,该产品的年销售量y(万件)与销售单价x(元)之间的函数关系式为y=25﹣0.5x,其中销售单价不低于25元且不高于45元.(第一年年获利=年销售收入﹣生产成本﹣投资成本,第二年年获利=年销售收入﹣生产成本)
(1)当销售单价定为28元时,该产品的年销售量为多少万件?
(2)求该公司第一年的年获利w(万元)与销售单价x(元)之间的函数关系式,由于投资金额较大,投资的第一年,该公司最小亏损是多少万元?并求此时的销售单价为多少元?
(3)填空:第二年,该公司决定给希望工程捐助款m万元,该项捐助款由两部分组成:一部分为10万元的固定捐款,另一部分则为每销售一件产品,就抽出一元钱作为捐款,若除去第一年的最小亏损金额以及第二年的捐助款后,到第二年年底,两年的总盈利等于67.5万元,请你确定第二年销售单价x的值为 .
科目:czsx 来源:2014-2015学年浙江省九年级下学期期中考试数学试卷(解析版) 题型:填空题
(本题12分)为了推进节能减排,发展低碳经济,温州市某公司以 25万元购得某项节能产品的生产技术后,再投入100万元购买生产设备,进行该产品的生产加工,已知生产这种产品的成本价为每件20元,经过市场调研发现,该产品的年销售量y(万件)与销售单价x(元)之间的函数关系式为y=25-0.5x,其中销售单价不低于25元且不高于45元.(第一年年获利=年销售收入-生产成本-投资成本,第二年年获利=年销售收入-生产成本)
(1)当销售单价定为28元时,该产品的年销售量为多少万件?
(2)求该公司第一年的年获利w(万元)与销售单价x(元)之间的函数关系式,由于投资金额较大,投资的第一年,该公司最小亏损是多少万元?并求此时的销售单价为多少元?
(3)填空:第二年,该公司决定给希望工程捐助款m万元,该项捐助款由两部分组成:一部分为10万元的固定捐款,另一部分则为每销售一件产品,就抽出一元钱作为捐款,若除去第一年的最小亏损金额以及第二年的捐助款后,到第二年年底,两年的总盈利等于67.5万元,请你确定第二年销售单价x的值为________.
科目:czsx 来源:2014-2015学年浙江省温州市瓯海区梧田片八校九年级5月联合模拟数学试卷(解析版) 题型:解答题
(本题12分)为了推进节能减排,发展低碳经济,温州市某公司以 25万元购得某项节能产品的生产技术后,再投入100万元购买生产设备,进行该产品的生产加工,已知生产这种产品的成本价为每件20元,经过市场调研发现,该产品的年销售量y(万件)与销售单价x(元)之间的函数关系式为y=25-0.5x,其中销售单价不低于25元且不高于45元.(第一年年获利=年销售收入-生产成本-投资成本,第二年年获利=年销售收入-生产成本)
(1)当销售单价定为28元时,该产品的年销售量为多少万件?
(2)求该公司第一年的年获利w(万元)与销售单价x(元)之间的函数关系式,由于投资金额较大,投资的第一年,该公司最小亏损是多少万元?并求此时的销售单价为多少元?
(3)填空:第二年,该公司决定给希望工程捐助款m万元,该项捐助款由两部分组成:一部分为10万元的固定捐款,另一部分则为每销售一件产品,就抽出一元钱作为捐款,若除去第一年的最小亏损金额以及第二年的捐助款后,到第二年年底,两年的总盈利等于67.5万元,请你确定第二年销售单价x的值为________.
科目:czsx 来源: 题型:
下列是由四个相同小正方体摆成的立方体图形,它的俯视图是( )
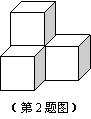
| A. B. C. D. |
1. 我州今年参加中考的学生人数大约为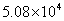 人,对于这个科学记数法表示的近似数,下列说法正确的是( )
人,对于这个科学记数法表示的近似数,下列说法正确的是( )
A.精确到百分位,有3个有效数字 B.精确到百分位,有5个有效数字
C.精确到百位,有3个有效数字 D.精确到百位,有5个有效数字
2. 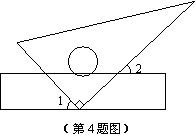 如图,将一块三角板的执教顶点放在直尺的一边上,当
如图,将一块三角板的执教顶点放在直尺的一边上,当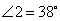 时,
时,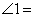 ( )
( )
A. B.
B.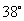 C.
C.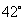 D.
D.
3. 下列根式中,不能与 合并的是( )
合并的是( )
A.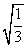 B.
B.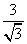 C.
C.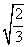 D.
D.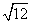
某班45名同学某天每人的生活费用统计如下表:
| 生活费(元) | 10 | 15 | 20 | 25 | 30 |
| 学生人数(人) | 4 | 10 | 15 | 10 | 6 |
对于这45名同学这天每人的生活费用,下列说法不正确的是( )A.平均数是20 B.众数 C.中位数是20 D.极差是2021世纪教育网版权所有
4. 关于 的一元二次方程
的一元二次方程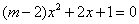 有实数根,则
有实数根,则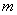 的取值范围是( )
的取值范围是( )
A.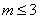 B.
B. C.
C. 且
且 D.
D.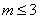 且
且
5. 将圆心角为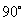 ,面积为
,面积为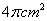 的扇形围成一个圆锥的侧面,则所围成圆锥的底面半径为( )
的扇形围成一个圆锥的侧面,则所围成圆锥的底面半径为( )
A.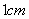 B.
B.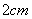 C.
C.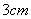 D.
D.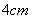
6. 在平面直角坐标系中,点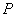 (
(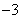 ,2)关于直线
,2)关于直线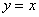 对称点的坐标是( )
对称点的坐标是( )
A.(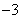 ,
,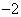 ) B.(3,2) C.(2,
) B.(3,2) C.(2,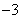 ) D.(3,
) D.(3,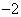 )
)
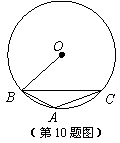
7. 如图,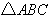 内接于
内接于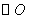 ,
,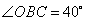 ,则
,则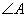 的度数为( )
的度数为( )
A.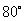 B.
B.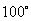 C.
C.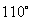 D.
D.
8. 以正方形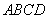 两条对角线的交点
两条对角线的交点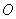 为坐标原点,建立如图所示的平面直角坐标系,双曲线
为坐标原点,建立如图所示的平面直角坐标系,双曲线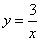 经过点
经过点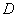 ,则正方形
,则正方形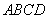 的面积是( )21·cn·jy·com
的面积是( )21·cn·jy·com
A.10 B.11 C.12 D.13
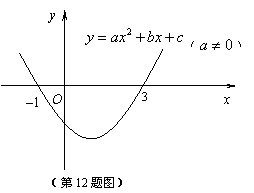
9. 二次函数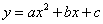 (
(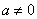 )的图象如图所示,下列说法:①
)的图象如图所示,下列说法:①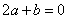 ;②当
;②当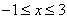 时,
时,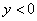 ;③若点(
;③若点(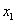 ,
,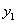 )和点(
)和点(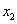 ,
,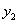 )都在函数的图象上,当
)都在函数的图象上,当 时,
时,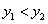 ;④
;④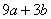
 。其中正确的是( )21·世纪*教育网
。其中正确的是( )21·世纪*教育网
A.① ② ④ B.① ④ C.① ② ③ D.③ ④

第II卷(选择题 共72分)
二、填空题:(共5个小题,每小题4分,共20分)
10. 的平方根是 。
的平方根是 。
11.已知函数 是正比例函数,则
是正比例函数,则 ,
,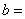 。
。
12.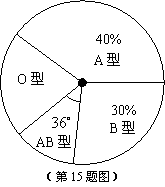 小明同学根据全班同学的血型绘制了如图所示的扇形统计图,已知
小明同学根据全班同学的血型绘制了如图所示的扇形统计图,已知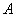 型血的有20人,则
型血的有20人,则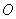 型血的有 人。21教育网
型血的有 人。21教育网
13.分式方程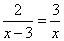 的解是 。
的解是 。
14.在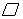
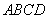 中,
中, 、
、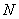 是
是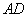 边上的三等分点,连接
边上的三等分点,连接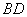 、
、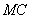 相交于
相交于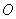 点,则
点,则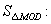
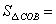 。2-1-c-n-j-y
。2-1-c-n-j-y
三、解答题:(共2小题,每小题6分,共12分)
15.计算: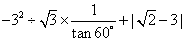 ;
;
16.先化简: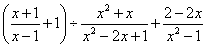 ,然后从
,然后从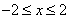 的范围内选取一个合适的整数作为
的范围内选取一个合适的整数作为 的值代入求值。
的值代入求值。
四、解答题:(共3小题,每小题8分,共24分)
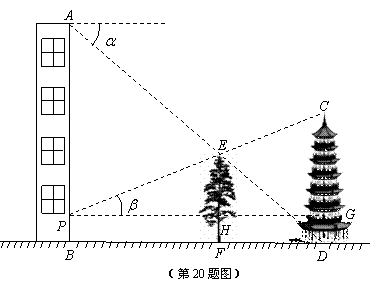
17.如图,在楼房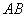 和塔
和塔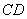 之间有一棵树
之间有一棵树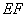 ,从楼顶
,从楼顶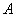 处经过树顶
处经过树顶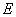 点恰好看到塔的底部
点恰好看到塔的底部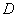 点,且俯角
点,且俯角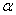 为
为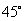 ,从楼底
,从楼底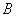 点1米的
点1米的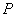 点处经过树顶
点处经过树顶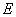 点恰好看到塔的顶部
点恰好看到塔的顶部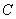 点,且仰角
点,且仰角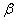 为
为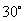 。已知树高
。已知树高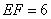 米,求塔
米,求塔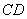 的高度(结果保留根号)。
的高度(结果保留根号)。
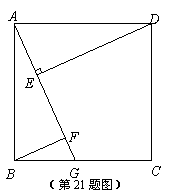
18.如图,在正方形 中,
中, 是
是 上任意一点,连接
上任意一点,连接 ,
,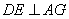 于
于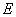 ,
,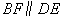 交
交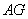 于
于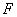 ,探究线段
,探究线段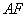 、
、 、
、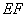 三者之间的数量关系,并说明理由。
三者之间的数量关系,并说明理由。
19.2015年5月6日,凉山州政府在邛海“空列”项目考察座谈会上与多方达成初步合作意向,决定共同出资60.8亿元,建设40千米的环邛海空中列车,这将是国内第一条空中列车。据计算,将有24千米的“空列”轨道假设在水上,其余假设在陆地上,并且每千米水上建设费用比陆地建设费用多0.2亿元。 21*cnjy*com
(1)求每千米 “空列”轨道的水上建设费用和陆地建设费用各需多少亿元?
(2)设计在某段“空列”轨道的建设中,每天至少需要运送沙石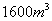 ,施工方准备租用大、小两种运输车共十辆。已知每辆大车每天运送沙石
,施工方准备租用大、小两种运输车共十辆。已知每辆大车每天运送沙石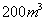 ,每辆小车每天运送沙石
,每辆小车每天运送沙石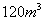 ,大、小车每天每辆租车费用分别是1000元,700元,且要求每天租车的总费用不得超过9300元,问施工方有几种租车方案?那种租车方案费用最低,最低费用是多少?
,大、小车每天每辆租车费用分别是1000元,700元,且要求每天租车的总费用不得超过9300元,问施工方有几种租车方案?那种租车方案费用最低,最低费用是多少?
五、解答题:(共2小题,每小题8分,共16分)
20.有甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0、1、2;乙袋中装有3个完全相同的小球,分别标有数字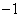 、
、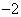 、0;先从甲袋中随机取出一个小球,记录标有的数字为
、0;先从甲袋中随机取出一个小球,记录标有的数字为 ,再从乙袋中随机取出一个小球,记录标有的数字为
,再从乙袋中随机取出一个小球,记录标有的数字为 ,确定点
,确定点 (
( ,
, )。www.21-cn-jy.com
)。www.21-cn-jy.com
(1)用树状图或列表法列举点 所有可能的坐标;
所有可能的坐标;
(2)求点 (
( ,
, )在函数
)在函数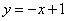 的图象上的概率 ;
的图象上的概率 ;
(3)在平面直角坐标系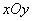 中,
中,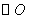 的半径是2,求过点
的半径是2,求过点 (
( ,
, )能作
)能作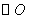 的切线的概率;
的切线的概率;
21.阅读理解:
材料1:一组对边平行,另一组对边不平行的四边形叫梯形。其中平行的两边叫做梯形的底边,不平行的两边叫做梯形的腰。连接梯形两腰中点的线段叫做梯形的中位线。
 梯形的中位线具有下列性质:
梯形的中位线具有下列性质:
梯形的中位线平行于两底,并且等于两底和的一半。
如图(1),在梯形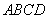 中,
中,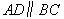 。
。
∵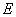 、
、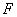 分别是
分别是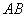 、
、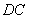 的中点,
的中点,
∴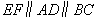 ,
,
 。
。
材料2:经过三角形一边的中点与另一边平行的直线必平分第三边。
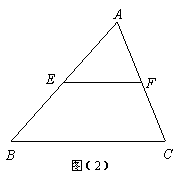
如图(2),在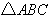 中,∵
中,∵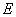 是
是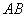 的中点,
的中点, ,
,
∴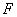 是
是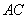 的中点。
的中点。
请你运用所学知识,结合上述材料,解答下列问题:
如图(3),在梯形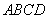 中,
中,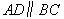 ,
,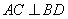 于
于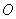 ,
,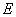 、
、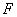 分别是
分别是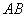 、
、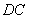 的中点,
的中点,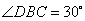 。
。
(1)求证: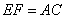 ;
;
(2)若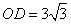 ,
,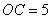 ,求
,求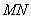 的长。
的长。

B卷(共30分)
 二、填空题:(共2小题,每小题5分,共10分)
二、填空题:(共2小题,每小题5分,共10分)
22.已知实数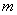 、
、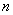 满足
满足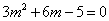 ,
,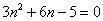 ,则
,则 。
。
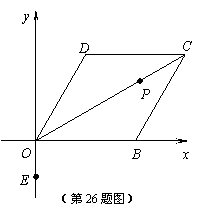
23.菱形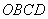 在平面直角坐标系中的位置如图所示,顶点
在平面直角坐标系中的位置如图所示,顶点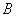 (2,0),
(2,0),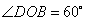 ,点
,点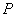 是对角线
是对角线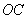 上一个动点,
上一个动点, 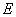 (0,
(0,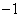 ),当
),当 最短时,点
最短时,点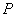 的坐标为 。2·1·c·n·j·y
的坐标为 。2·1·c·n·j·y
二、解答题:(共2小题,27题8分,28题12分,共20分)
24.如图,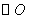 的半径为5,点
的半径为5,点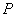 在
在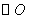 外,
外,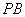 交
交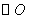 于
于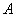 、
、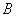 两点,
两点,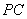 交
交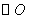 于
于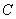 、
、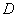 两点。
两点。
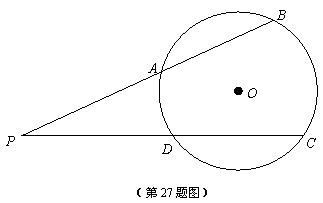 (1)求证:
(1)求证: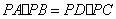 ;(2)若
;(2)若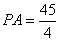 ,
,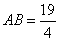 ,
,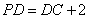 ,求点
,求点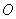 到
到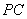 的距离。
的距离。
25.如图,已知抛物线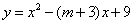 的顶点
的顶点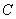 在
在 轴的正半轴上,一次函数
轴的正半轴上,一次函数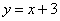 与抛物线交于
与抛物线交于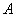 、
、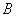 两点,与
两点,与 、
、 轴分别交于
轴分别交于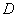 、
、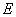 两点。
两点。
(1)求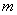 的值;
的值;
(2)求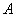 、
、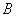 两点的坐标;
两点的坐标;
(3)点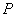 (
(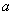 ,
,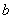 )(
)(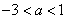 )是抛物线上一点,当
)是抛物线上一点,当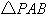 得面积是
得面积是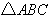 面积的2倍时,求
面积的2倍时,求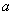 、
、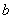 的值。
的值。
科目:czsx 来源:河北省模拟题 题型:解答题
| 某县决定鼓励农民开荒种植牡丹并实行政府补贴,规定每新种植一亩牡丹一次性补贴农户若干元经调查,种植亩数y(亩)与补贴数额x(元)之间成一次函数关系,且补贴与种植情况如下表: | ||||||||
(1)分别求出政府补贴政策实施后,种植亩数y(亩)、每亩牡丹的收益z(元)与政府补贴数额x(元)之间的函数关系式; (2)要使全县新种植的牡丹总收益W(元)最大,又要从政府的角度出发,政府应将每亩补贴数额x定为多少元?并求出总收益W的最大值和此时种植亩数;(总收益=每亩收益×亩数) (3)在(2)问中取得最大总收益的情况下,需占用其中不超过50亩的新种牡丹园,利用其树间空地种植新品种“黑桃皇后”已知引进该新品种平均每亩的费用为530元,此外还要购置其它设备,这项费用(元)等于种植面积(亩)的平方的25倍这样混种了“黑桃皇后”的这部分土地比原来种植单一品种牡丹时每亩的平均收益增加了2000元,这部分混种土地在扣除所有费用后总收益为85000元,求混种牡丹的土地有多少亩? |
科目:czsx 来源: 题型:阅读理解
| 补贴数额x(元) | 100 | 200 | … |
| 种植亩数y(亩) | 1600 | 2400 | … |
| 2 |
| 3 |
| 5 |
科目:czsx 来源: 题型:解答题
| 补贴数额x(元) | 100 | 200 | … |
| 种植亩数y(亩) | 1600 | 2400 | … |
 =1.414,
=1.414, =1.732,
=1.732, =2.236)
=2.236) 科目:czsx 来源:2012年重庆市中考数学限时训练试卷(五)(解析版) 题型:解答题
| 补贴数额x(元) | 100 | 200 | … |
| 种植亩数y(亩) | 1600 | 2400 | … |
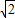 =1.414,
=1.414, =1.732,
=1.732,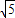 =2.236)
=2.236)科目:czsx 来源:2012年重庆市中考数学模拟试卷(二)(解析版) 题型:解答题
| 补贴数额x(元) | 100 | 200 | … |
| 种植亩数y(亩) | 1600 | 2400 | … |
 =1.414,
=1.414,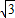 =1.732,
=1.732, =2.236)
=2.236)科目:czsx 来源: 题型:阅读理解
重庆市垫江县具有2000多年的牡丹种植历史.每年3月下旬至4月上旬,主要分布在该县太平镇、澄溪镇明月山一带的牡丹迎春怒放,美不胜收.由于牡丹之根———丹皮是重要中药材,目前已种植有60多个品种2万余亩牡丹的垫江,因此成为我国丹皮出口基地,获得“丹皮之乡”的美誉。为了提高农户收入,该县决定在现有基础上开荒种植牡丹并实行政府补贴,规定每新种植一亩牡丹一次性补贴农户若干元,经调查,种植亩数![]() (亩)与补贴数额
(亩)与补贴数额![]() (元)之间成一次函数关系,且补贴与种植情况如下表:
(元)之间成一次函数关系,且补贴与种植情况如下表:
| 补贴数额(元) | 10 | 20 | …… |
| 种植亩数(亩) | 160 | 240 | …… |
随着补贴数额![]() 的不断增大,种植规模也不断增加,但每亩牡丹的收益
的不断增大,种植规模也不断增加,但每亩牡丹的收益![]() (元)会相应降低,且该县补贴政策实施前每亩牡丹的收益为3000元,而每补贴10元(补贴数为10元的整数倍),每亩牡丹的收益会相应减少30元.
(元)会相应降低,且该县补贴政策实施前每亩牡丹的收益为3000元,而每补贴10元(补贴数为10元的整数倍),每亩牡丹的收益会相应减少30元.
(1)分别求出政府补贴政策实施后,种植亩数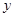 (亩)、每亩牡丹的收益
(亩)、每亩牡丹的收益![]() (元)与政府补贴数额
(元)与政府补贴数额![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)要使全县新种植的牡丹总收益![]() (元)最大,又要从政府的角度出发,政府应将每亩补贴数额
(元)最大,又要从政府的角度出发,政府应将每亩补贴数额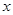 定为多少元?并求出总收益
定为多少元?并求出总收益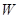 的最大值和此时种植亩数;(总收益=每亩收益×亩数)
的最大值和此时种植亩数;(总收益=每亩收益×亩数)
(3)在(2)问中取得最大总收益的情况下,为了发展旅游业,需占用其中不超过50亩的新种牡丹园,利用其树间空地种植刚由国际牡丹园培育出的“黑桃皇后”.已知引进该新品种平均每亩的费用为530元,此外还要购置其它设备,这项费用(元)等于种植面积(亩)的平方的25倍.这样混种了“黑桃皇后”的这部分土地比原来种植单一品种牡丹时每亩的平均收益增加了2000元,这部分混种土地在扣除所有费用后总收益为85000元.求混种牡丹的土地有多少亩?(结果精确到个位)(参考数据:![]() )
)
科目:czsx 来源: 题型:阅读理解
重庆市垫江县具有2000多年的牡丹种植历史.每年3月下旬至4月上旬,主要分布在该县太平镇、澄溪镇明月山一带的牡丹迎春怒放,美不胜收.由于牡丹之根———丹皮是重要中药材,目前已种植有60多个品种2万余亩牡丹的垫江,因此成为我国丹皮出口基地,获得“丹皮之乡”的美誉。为了提高农户收入,该县决定在现有基础上开荒种植牡丹并实行政府补贴,规定每新种植一亩牡丹一次性补贴农户若干元,经调查,种植亩数![]() (亩)与补贴数额
(亩)与补贴数额![]() (元)之间成一次函数关系,且补贴与种植情况如下表:
(元)之间成一次函数关系,且补贴与种植情况如下表:
| 补贴数额(元) | 10 | 20 | …… |
| 种植亩数(亩) | 160 | 240 | …… |
随着补贴数额![]() 的不断增大,种植规模也不断增加,但每亩牡丹的收益
的不断增大,种植规模也不断增加,但每亩牡丹的收益![]() (元)会相应降低,且该县补贴政策实施前每亩牡丹的收益为3000元,而每补贴10元(补贴数为10元的整数倍),每亩牡丹的收益会相应减少30元.
(元)会相应降低,且该县补贴政策实施前每亩牡丹的收益为3000元,而每补贴10元(补贴数为10元的整数倍),每亩牡丹的收益会相应减少30元.
(1)分别求出政府补贴政策实施后,种植亩数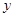 (亩)、每亩牡丹的收益
(亩)、每亩牡丹的收益![]() (元)与政府补贴数额
(元)与政府补贴数额![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)要使全县新种植的牡丹总收益![]() (元)最大,又要从政府的角度出发,政府应将每亩补贴数额
(元)最大,又要从政府的角度出发,政府应将每亩补贴数额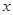 定为多少元?并求出总收益
定为多少元?并求出总收益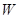 的最大值和此时种植亩数;(总收益=每亩收益×亩数)
的最大值和此时种植亩数;(总收益=每亩收益×亩数)
(3)在(2)问中取得最大总收益的情况下,为了发展旅游业,需占用其中不超过50亩的新种牡丹园,利用其树间空地种植刚由国际牡丹园培育出的“黑桃皇后”.已知引进该新品种平均每亩的费用为530元,此外还要购置其它设备,这项费用(元)等于种植面积(亩)的平方的25倍.这样混种了“黑桃皇后”的这部分土地比原来种植单一品种牡丹时每亩的平均收益增加了2000元,这部分混种土地在扣除所有费用后总收益为85000元.求混种牡丹的土地有多少亩?(结果精确到个位)(参考数据:![]() )
)
科目:czsx 来源: 题型:阅读理解
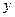 (亩)与补贴数额
(亩)与补贴数额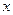 (元)之间成一次函数关系,且补贴与种植情况如下表:
(元)之间成一次函数关系,且补贴与种植情况如下表:| 补贴数额(元) | 10 | 20 | …… |
| 种植亩数(亩) | 160 | 240 | …… |
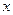 的不断增大,种植规模也不断增加,但每亩牡丹的收益
的不断增大,种植规模也不断增加,但每亩牡丹的收益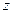 (元)会相应降低,且该县补贴政策实施前每亩牡丹的收益为3000元,而每补贴10元(补贴数为10元的整数倍),每亩牡丹的收益会相应减少30元.
(元)会相应降低,且该县补贴政策实施前每亩牡丹的收益为3000元,而每补贴10元(补贴数为10元的整数倍),每亩牡丹的收益会相应减少30元.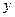 (亩)、每亩牡丹的收益
(亩)、每亩牡丹的收益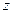 (元)与政府补贴数额
(元)与政府补贴数额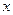 (元)之间的函数关系式;
(元)之间的函数关系式;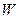 (元)最大,又要从政府的角度出发,政府应将每亩补贴数额
(元)最大,又要从政府的角度出发,政府应将每亩补贴数额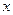 定为多少元?并求出总收益
定为多少元?并求出总收益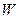 的最大值和此时种植亩数;(总收益=每亩收益×亩数)
的最大值和此时种植亩数;(总收益=每亩收益×亩数)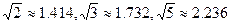 )
) 科目:czsx 来源:2011年河南省周口市初一下学期相交线与平行线专项训练 题型:解答题
重庆市垫江县具有2000多年的牡丹种植历史.每年3月下旬至4月上旬,主要分布在该县太平镇、澄溪镇明月山一带的牡丹迎春怒放,美不胜收.由于牡丹之根———丹皮是重要中药材,目前已种植有60多个品种2万余亩牡丹的垫江,因此成为我国丹皮出口基地,获得“丹皮之乡”的美誉。为了提高农户收入,该县决定在现有基础上开荒种植牡丹并实行政府补贴,规定每新种植一亩牡丹一次性补贴农户若干元,经调查,种植亩数 (亩)与补贴数额
(亩)与补贴数额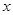 (元)之间成一次函数关系,且补贴与种植情况如下表:
(元)之间成一次函数关系,且补贴与种植情况如下表:
|
补贴数额(元) |
10 |
20 |
…… |
|
种植亩数(亩) |
160 |
240 |
…… |
随着补贴数额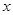 的不断增大,种植规模也不断增加,但每亩牡丹的收益
的不断增大,种植规模也不断增加,但每亩牡丹的收益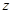 (元)会相应降低,且该县补贴政策实施前每亩牡丹的收益为3000元,而每补贴10元(补贴数为10元的整数倍),每亩牡丹的收益会相应减少30元.
(元)会相应降低,且该县补贴政策实施前每亩牡丹的收益为3000元,而每补贴10元(补贴数为10元的整数倍),每亩牡丹的收益会相应减少30元.
(1)分别求出政府补贴政策实施后,种植亩数 (亩)、每亩牡丹的收益
(亩)、每亩牡丹的收益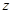 (元)与政府补贴数额
(元)与政府补贴数额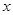 (元)之间的函数关系式;
(元)之间的函数关系式;
(2)要使全县新种植的牡丹总收益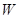 (元)最大,又要从政府的角度出发,政府应将每亩补贴数额
(元)最大,又要从政府的角度出发,政府应将每亩补贴数额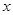 定为多少元?并求出总收益
定为多少元?并求出总收益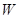 的最大值和此时种植亩数;(总收益=每亩收益×亩数)
的最大值和此时种植亩数;(总收益=每亩收益×亩数)
(3)在(2)问中取得最大总收益的情况下,为了发展旅游业,需占用其中不超过50亩的新种牡丹园,利用其树间空地种植刚由国际牡丹园培育出的“黑桃皇后”.已知引进该新品种平均每亩的费用为530元,此外还要购置其它设备,这项费用(元)等于种植面积(亩)的平方的25倍.这样混种了“黑桃皇后”的这部分土地比原来种植单一品种牡丹时每亩的平均收益增加了2000元,这部分混种土地在扣除所有费用后总收益为85000元.求混种牡丹的土地有多少亩?(结果精确到个位)(参考数据: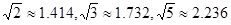 )
)
科目:czsx 来源:2011年河南省周口市初一下学期平移专项训练 题型:解答题
重庆市垫江县具有2000多年的牡丹种植历史.每年3月下旬至4月上旬,主要分布在该县太平镇、澄溪镇明月山一带的牡丹迎春怒放,美不胜收.由于牡丹之根———丹皮是重要中药材,目前已种植有60多个品种2万余亩牡丹的垫江,因此成为我国丹皮出口基地,获得“丹皮之乡”的美誉。为了提高农户收入,该县决定在现有基础上开荒种植牡丹并实行政府补贴,规定每新种植一亩牡丹一次性补贴农户若干元,经调查,种植亩数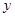 (亩)与补贴数额
(亩)与补贴数额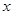 (元)之间成一次函数关系,且补贴与种植情况如下表:
(元)之间成一次函数关系,且补贴与种植情况如下表:
|
补贴数额(元) |
10 |
20 |
…… |
|
种植亩数(亩) |
160 |
240 |
…… |
随着补贴数额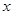 的不断增大,种植规模也不断增加,但每亩牡丹的收益
的不断增大,种植规模也不断增加,但每亩牡丹的收益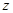 (元)会相应降低,且该县补贴政策实施前每亩牡丹的收益为3000元,而每补贴10元(补贴数为10元的整数倍),每亩牡丹的收益会相应减少30元.
(元)会相应降低,且该县补贴政策实施前每亩牡丹的收益为3000元,而每补贴10元(补贴数为10元的整数倍),每亩牡丹的收益会相应减少30元.
(1)分别求出政府补贴政策实施后,种植亩数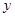 (亩)、每亩牡丹的收益
(亩)、每亩牡丹的收益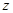 (元)与政府补贴数额
(元)与政府补贴数额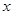 (元)之间的函数关系式;
(元)之间的函数关系式;
(2)要使全县新种植的牡丹总收益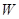 (元)最大,又要从政府的角度出发,政府应将每亩补贴数额
(元)最大,又要从政府的角度出发,政府应将每亩补贴数额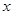 定为多少元?并求出总收益
定为多少元?并求出总收益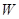 的最大值和此时种植亩数;(总收益=每亩收益×亩数)
的最大值和此时种植亩数;(总收益=每亩收益×亩数)
(3)在(2)问中取得最大总收益的情况下,为了发展旅游业,需占用其中不超过50亩的新种牡丹园,利用其树间空地种植刚由国际牡丹园培育出的“黑桃皇后”.已知引进该新品种平均每亩的费用为530元,此外还要购置其它设备,这项费用(元)等于种植面积(亩)的平方的25倍.这样混种了“黑桃皇后”的这部分土地比原来种植单一品种牡丹时每亩的平均收益增加了2000元,这部分混种土地在扣除所有费用后总收益为85000元.求混种牡丹的土地有多少亩?(结果精确到个位)(参考数据: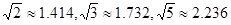 )
)
科目:czsx 来源:不详 题型:解答题
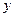 (亩)与补贴数额
(亩)与补贴数额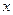 (元)之间成一次函数关系,且补贴与种植情况如下表:
(元)之间成一次函数关系,且补贴与种植情况如下表:| 补贴数额(元) | 10 | 20 | …… |
| 种植亩数(亩) | 160 | 240 | …… |
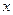 的不断增大,种植规模也不断增加,但每亩牡丹的收益
的不断增大,种植规模也不断增加,但每亩牡丹的收益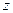 (元)会相应降低,且该县补贴政策实施前每亩牡丹的收益为3000元,而每补贴10元(补贴数为10元的整数倍),每亩牡丹的收益会相应减少30元.
(元)会相应降低,且该县补贴政策实施前每亩牡丹的收益为3000元,而每补贴10元(补贴数为10元的整数倍),每亩牡丹的收益会相应减少30元.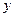 (亩)、每亩牡丹的收益
(亩)、每亩牡丹的收益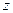 (元)与政府补贴数额
(元)与政府补贴数额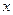 (元)之间的函数关系式;
(元)之间的函数关系式;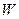 (元)最大,又要从政府的角度出发,政府应将每亩补贴数额
(元)最大,又要从政府的角度出发,政府应将每亩补贴数额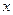 定为多少元?并求出总收益
定为多少元?并求出总收益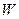 的最大值和此时种植亩数;(总收益=每亩收益×亩数)
的最大值和此时种植亩数;(总收益=每亩收益×亩数)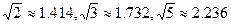 )
)科目:czsx 来源:2011年河南省周口市初一下学期平移专项训练 题型:解答题
重庆市垫江县具有2000多年的牡丹种植历史.每年3月下旬至4月上旬,主要分布在该县太平镇、澄溪镇明月山一带的牡丹迎春怒放,美不胜收.由于牡丹之根———丹皮是重要中药材,目前已种植有60多个品种2万余亩牡丹的垫江,因此成为我国丹皮出口基地,获得“丹皮之乡”的美誉。为了提高农户收入,该县决定在现有基础上开荒种植牡丹并实行政府补贴,规定每新种植一亩牡丹一次性补贴农户若干元,经调查,种植亩数 (亩)与补贴数额
(亩)与补贴数额 (元)之间成一次函数关系,且补贴与种植情况如下表:
(元)之间成一次函数关系,且补贴与种植情况如下表:
| 补贴数额(元) | 10 | 20 | …… |
| 种植亩数(亩) | 160 | 240 | …… |
 的不断增大,种植规模也不断增加,但每亩牡丹的收益
的不断增大,种植规模也不断增加,但每亩牡丹的收益 (元)会相应降低,且该县补贴政策实施前每亩牡丹的收益为3000元,而每补贴10元(补贴数为10元的整数倍),每亩牡丹的收益会相应减少30元.
(元)会相应降低,且该县补贴政策实施前每亩牡丹的收益为3000元,而每补贴10元(补贴数为10元的整数倍),每亩牡丹的收益会相应减少30元. (亩)、每亩牡丹的收益
(亩)、每亩牡丹的收益 (元)与政府补贴数额
(元)与政府补贴数额 (元)之间的函数关系式;
(元)之间的函数关系式; (元)最大,又要从政府的角度出发,政府应将每亩补贴数额
(元)最大,又要从政府的角度出发,政府应将每亩补贴数额 定为多少元?并求出总收益
定为多少元?并求出总收益 的最大值和此时种植亩数;(总收益=每亩收益×亩数)
的最大值和此时种植亩数;(总收益=每亩收益×亩数) )
)