科目:gzsx
来源:
题型:
已知函数f(x)=a•lnx+b•x
2在点(1,f(1))处的切线方程为x-y-1=0.
(1)求f(x)的表达式;
(2)若f(x)满足f(x)≥g(x)恒成立,则称f(x)是g(x)的一个“上界函数”,如果函数
f(x)为g(x)=-lnx(t为实数)的一个“上界函数”,求t的取值范围;
(3)当m>0时,讨论
F(x)=f(x)+-x在区间(0,2)上极值点的个数.
查看答案和解析>>
科目:gzsx
来源:
题型:解答题
已知函数f(x)=a•lnx+b•x2在点(1,f(1))处的切线方程为x-y-1=0.
(1)求f(x)的表达式;
(2)若f(x)满足f(x)≥g(x)恒成立,则称f(x)是g(x)的一个“上界函数”,如果函数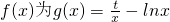 (t为实数)的一个“上界函数”,求t的取值范围;
(t为实数)的一个“上界函数”,求t的取值范围;
(3)当m>0时,讨论 在区间(0,2)上极值点的个数.
在区间(0,2)上极值点的个数.
查看答案和解析>>
科目:gzsx
来源:2013年高考数学仿真模拟试卷12(解析版)
题型:解答题
已知函数f(x)=a•lnx+b•x
2在点(1,f(1))处的切线方程为x-y-1=0.
(1)求f(x)的表达式;
(2)若f(x)满足f(x)≥g(x)恒成立,则称f(x)是g(x)的一个“上界函数”,如果函数

(t为实数)的一个“上界函数”,求t的取值范围;
(3)当m>0时,讨论

在区间(0,2)上极值点的个数.
查看答案和解析>>
科目:gzsx
来源:2012-2013学年江西省吉安一中高三(上)期中数学试卷(文科)(解析版)
题型:解答题
已知函数f(x)=a•lnx+b•x
2在点(1,f(1))处的切线方程为x-y-1=0.
(1)求f(x)的表达式;
(2)若f(x)满足f(x)≥g(x)恒成立,则称f(x)是g(x)的一个“上界函数”,如果函数

(t为实数)的一个“上界函数”,求t的取值范围;
(3)当m>0时,讨论

在区间(0,2)上极值点的个数.
查看答案和解析>>
科目:gzsx
来源:2011年山东省济宁市高考数学模拟试卷(理科)(解析版)
题型:解答题
已知函数f(x)=a•lnx+b•x
2在点(1,f(1))处的切线方程为x-y-1=0.
(1)求f(x)的表达式;
(2)若f(x)满足f(x)≥g(x)恒成立,则称f(x)是g(x)的一个“上界函数”,如果函数

(t为实数)的一个“上界函数”,求t的取值范围;
(3)当m>0时,讨论
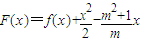
在区间(0,2)上极值点的个数.
查看答案和解析>>
科目:gzsx
来源:
题型:
已知:函数f(x)=a•lnx+bx
2+x在点(f,f(1))处的切线方程为x-y-1=0.
(1)求f(x)的表达式;
(2)设函数
y=f(x)+的反函数为p(x),t(x)=p(x)(1-x),求函数t(x)的最大值;
(3)在(2)中,问是否存在正整数N,使得当n∈N
+且n>N时,不等式
p(-1)+p(-)+p(-) +p(-) <n-2011恒成立?若存在,请找出一个满足条件的N的值,并给以说明;若不存在,请说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:解答题
已知:函数f(x)=a•lnx+bx2+x在点(f,f(1))处的切线方程为x-y-1=0.
(1)求f(x)的表达式;
(2)设函数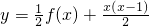 的反函数为p(x),t(x)=p(x)(1-x),求函数t(x)的最大值;
的反函数为p(x),t(x)=p(x)(1-x),求函数t(x)的最大值;
(3)在(2)中,问是否存在正整数N,使得当n∈N+且n>N时,不等式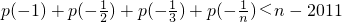 恒成立?若存在,请找出一个满足条件的N的值,并给以说明;若不存在,请说明理由.
恒成立?若存在,请找出一个满足条件的N的值,并给以说明;若不存在,请说明理由.
查看答案和解析>>
科目:gzsx
来源:2011-2012学年河北省保定市高三(上)摸底数学试卷(理科)(解析版)
题型:解答题
已知:函数f(x)=a•lnx+bx
2+x在点(f,f(1))处的切线方程为x-y-1=0.
(1)求f(x)的表达式;
(2)设函数
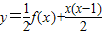
的反函数为p(x),t(x)=p(x)(1-x),求函数t(x)的最大值;
(3)在(2)中,问是否存在正整数N,使得当n∈N
+且n>N时,不等式
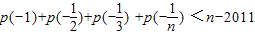
恒成立?若存在,请找出一个满足条件的N的值,并给以说明;若不存在,请说明理由.
查看答案和解析>>
科目:gzsx
来源:
题型:选择题
15.已知函数f(x)的图象在点(x
0,f(x
0))处的切线方程l:y=g(x),若函数f(x)满足∀x∈l(其中I为函数f(x)的定义域),当x≠x
0时,[f(x)-g(x)](x-x
0)>0恒成立,则称x
0为函数f(x)的“转折点”,若函数f(x)=lnx-ax
2-x在(0,e]上存在一个“转折点”,则a的取值范围为( )
| A. | $[{\frac{1}{{2{e^2}}},+∞})$ | | B. | $({-1,\frac{1}{{2{e^2}}}}]$ | | C. | $[{-\frac{1}{{2{e^2}}},1})$ | | D. | $({-∞,-\frac{1}{{2{e^2}}}}]$ |
查看答案和解析>>
科目:gzsx
来源:
题型:解答题
已知函数f(x)=ax•lnx+b(a,b∈R),在点(e,f(e))处的切线方程是2x-y-e=0(e为自然对数的底).
(1)求实数a,b的值及f(x)的解析式;
(2)若t是正数,设h(x)=f(x)+f(t-x),求h(x)的最小值;
(3)若关于x的不等式xlnx+(6-x)ln(6-x)≥ln(k2-72k)对一切x∈(0,6)恒成立,求实数k的取值范围.
查看答案和解析>>
科目:gzsx
来源:2011-2012学年广东省广州市真光中学等六校协作体高三第二次联考数学试卷(文科)(解析版)
题型:解答题
已知函数f(x)=ax•lnx+b(a,b∈R),在点(e,f(e))处的切线方程是2x-y-e=0(e为自然对数的底).
(1)求实数a,b的值及f(x)的解析式;
(2)若t是正数,设h(x)=f(x)+f(t-x),求h(x)的最小值;
(3)若关于x的不等式xlnx+(6-x)ln(6-x)≥ln(k2-72k)对一切x∈(0,6)恒成立,求实数k的取值范围.
查看答案和解析>>
科目:gzsx
来源:2011-2012学年广东省广州市真光中学等六校协作体高三第二次联考数学试卷(理科)(解析版)
题型:解答题
已知函数f(x)=ax•lnx+b(a,b∈R),在点(e,f(e))处的切线方程是2x-y-e=0(e为自然对数的底).
(1)求实数a,b的值及f(x)的解析式;
(2)若t是正数,设h(x)=f(x)+f(t-x),求h(x)的最小值;
(3)若关于x的不等式xlnx+(6-x)ln(6-x)≥ln(k2-72k)对一切x∈(0,6)恒成立,求实数k的取值范围.
查看答案和解析>>
科目:gzsx
来源:广东模拟
题型:解答题
已知函数f(x)=ax•lnx+b(a,b∈R),在点(e,f(e))处的切线方程是2x-y-e=0(e为自然对数的底).
(1)求实数a,b的值及f(x)的解析式;
(2)若t是正数,设h(x)=f(x)+f(t-x),求h(x)的最小值;
(3)若关于x的不等式xlnx+(6-x)ln(6-x)≥ln(k2-72k)对一切x∈(0,6)恒成立,求实数k的取值范围.
查看答案和解析>>
科目:gzsx
来源:2010-2011学年江西省吉安一中高二(下)第二次段考数学试卷(理科)(解析版)
题型:解答题
已知函数f(x)=ax+

+c(a>0)的图象在点(1,f(1))处的切线方程为y=x-1.
(1)试用a表示出b,c;
(2)若f(x)≥lnx在[1,+∞)上恒成立,求a的取值范围;
(3)证明:1+

+

+…+

>ln(n+1)+
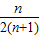
(n≥1).
查看答案和解析>>
科目:gzsx
来源:2010-2011学年湖北省咸宁市赤壁市南鄂高中高二(下)期末数学试卷2(理科)(解析版)
题型:解答题
已知函数f(x)=ax+

+c(a>0)的图象在点(1,f(1))处的切线方程为y=x-1.
(1)试用a表示出b,c;
(2)若f(x)≥lnx在[1,+∞)上恒成立,求a的取值范围;
(3)证明:1+

+

+…+

>ln(n+1)+

(n≥1).
查看答案和解析>>
科目:gzsx
来源:2013年高考数学压轴大题训练:函数图象的切线问题(解析版)
题型:解答题
已知函数f(x)=ax+

+c(a>0)的图象在点(1,f(1))处的切线方程为y=x-1.
(1)试用a表示出b,c;
(2)若f(x)≥lnx在[1,+∞)上恒成立,求a的取值范围;
(3)证明:1+

+

+…+

>ln(n+1)+

(n≥1).
查看答案和解析>>
科目:gzsx
来源:
题型:
已知函数f(x)=ax+
+c(a>0)的图象在点(1,f(1))处的切线方程为y=x-1.
(1)用a表示出b,c;
(2)若f(x)≥lnx在[1,+∞)上恒成立,求a的取值范围.
查看答案和解析>>
科目:gzsx
来源:广州三模
题型:解答题
已知函数f(x)=ax+
+c(a>0)的图象在点(1,f(1))处的切线方程为y=x-1.
(1)试用a表示出b,c;
(2)若f(x)≥lnx在[1,+∞)上恒成立,求a的取值范围;
(3)证明:1+
+
+…+
>ln(n+1)+
(n≥1).
查看答案和解析>>
科目:gzsx
来源:
题型:
设函数
f(x)=lnx-ax2-bx.
(1)已知f(x)在点P(1,f(1))处的切线方程是y=2x-1,求实数a,b的值.
(2)若方程f(x)=λx
2(λ>0)有唯一实数解,求实数λ的值.
查看答案和解析>>

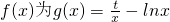 (t为实数)的一个“上界函数”,求t的取值范围;
(t为实数)的一个“上界函数”,求t的取值范围; 在区间(0,2)上极值点的个数.
在区间(0,2)上极值点的个数. (t为实数)的一个“上界函数”,求t的取值范围;
(t为实数)的一个“上界函数”,求t的取值范围; 在区间(0,2)上极值点的个数.
在区间(0,2)上极值点的个数. (t为实数)的一个“上界函数”,求t的取值范围;
(t为实数)的一个“上界函数”,求t的取值范围; 在区间(0,2)上极值点的个数.
在区间(0,2)上极值点的个数. (t为实数)的一个“上界函数”,求t的取值范围;
(t为实数)的一个“上界函数”,求t的取值范围;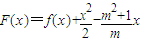 在区间(0,2)上极值点的个数.
在区间(0,2)上极值点的个数.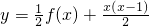 的反函数为p(x),t(x)=p(x)(1-x),求函数t(x)的最大值;
的反函数为p(x),t(x)=p(x)(1-x),求函数t(x)的最大值;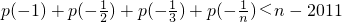 恒成立?若存在,请找出一个满足条件的N的值,并给以说明;若不存在,请说明理由.
恒成立?若存在,请找出一个满足条件的N的值,并给以说明;若不存在,请说明理由.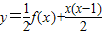 的反函数为p(x),t(x)=p(x)(1-x),求函数t(x)的最大值;
的反函数为p(x),t(x)=p(x)(1-x),求函数t(x)的最大值;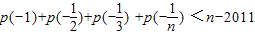 恒成立?若存在,请找出一个满足条件的N的值,并给以说明;若不存在,请说明理由.
恒成立?若存在,请找出一个满足条件的N的值,并给以说明;若不存在,请说明理由.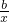 +c(a>0)的图象在点(1,f(1))处的切线方程为y=x-1.
+c(a>0)的图象在点(1,f(1))处的切线方程为y=x-1. +
+ +L+
+L+ >ln(n+1)+
>ln(n+1)+ (n≥1).
(n≥1). +c(a>0)的图象在点(1,f(1))处的切线方程为y=x-1.
+c(a>0)的图象在点(1,f(1))处的切线方程为y=x-1. +
+ +…+
+…+ >ln(n+1)+
>ln(n+1)+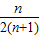 (n≥1).
(n≥1). +c(a>0)的图象在点(1,f(1))处的切线方程为y=x-1.
+c(a>0)的图象在点(1,f(1))处的切线方程为y=x-1. +
+ +…+
+…+ >ln(n+1)+
>ln(n+1)+ (n≥1).
(n≥1). +c(a>0)的图象在点(1,f(1))处的切线方程为y=x-1.
+c(a>0)的图象在点(1,f(1))处的切线方程为y=x-1. +
+ +…+
+…+ >ln(n+1)+
>ln(n+1)+ (n≥1).
(n≥1).