分析:(1)把x=1代入切线方程得到y=0,得到切点坐标,把切点坐标代入f(x)中,解得b的值,求出f(x)的导函数,把b的值代入后,再根据′(1)=1,求出a的值,把a与b的值代入即可确定出f(x);
(2)把(1)求出的f(x)和g(x)的解析式代入题中的不等式中,不等式要恒成立,即要当x大于0时,t小于等于一个关系式,设这个关系式为一个函数h(x),求出h(x)的导函数,令导函数等于0求出x的值,利用x的值分区间讨论导函数的正负,得到函数h(x)的单调区间,根据函数的增减性得到h(x)的最小值,进而得到t的取值范围;
(3)把(1)中求出的f(x)代入确定出F(x)的解析式,求出F(x)的导函数,令导函数等于0,得到x+
等于一个关系式,设y=x+
,且x大于0小于2,画出该函数的图象,如图所示,然后分m=1,m大于
小于2,m大于0小于等于
和m大于等于2,四种情况,根据函数的图象,即可得到相应区间上极值点的个数.
解答:解:(1)当x=1时,y=0,代入f(x)=a•lnx+b•x
2,可得:b=0,
所以f′(x)=
,由切线方程知f′(1)=1,所以a=1,
因此a=1,b=0,所以f(x)=lnx;
(2)把f(x)和g(x)的解析式代入得:
-lnx≤lnx恒成立,
因为x>0,所以只需要t≤2xlnx在(0,+∞)恒成立即可,
令h(x)=2xlnx,则h′(x)=2(1+lnx),
当x∈(0,
)时,h′(x)<0,所以h(x)在(0,
)上是减函数,
当x∈(
,+∞)时,h′(x)>0,所以h(x)在(
,+∞)上是增函数,
所以h(x)
min=h(
)=-
,所以t≤-
;
(3)由已知得F(x)=lnx+
-
x,所以F′(x)=
+x-
,
令F′(x)=0,得到
+x=
,令y=x+
,x∈(0,2),
画出该函数的图象,如图所示:
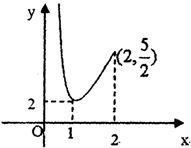
①当
=2,即m=1时,F′(x)=0在区间(0,2)上只有一个根1,且在1的两侧,
x+
>2,即在1的两侧F′(x)同正,此时F(x)在(0,2)上无极值点;
②当2<
<
,即
<m<2,且m≠1时,F′(x)=0在区间(0,2)上有两个不等根,
不妨设为x
1,x
2,且x
1<x
2,从图象上看在x
1和x
2两侧F′(x)=x+
-
都是异号的,
因此x
1和x
2都是F(x)的极值点,此时F(x)在(0,2)上有两个极值点;
③当
,即0<m≤
时,方程在区间(0,2)上只有一个根m,
由该方程所对应的二次函数图象可知,F′(x)在m两侧的符号不同,
因此函数F(x)在区间(0,2)上只有一个极值点;
④当
,即m≥2时,方程在区间(0,2)上只有一个根
,
由该方程所对应的二次函数图象可知,F′(x)在
两侧的符号不同,
因而函数F(x)在区间(0,2)上只有一个极值点,
综上,当m=1时,函数F(x)在区间(0,2)上无极值点;
当m∈(0,
)∪[2,+∞)时,函数F(x)在区间(0,2)上有一个极值点;
当m∈(
,1)∪(1,2)时,函数F(x)在区间(0,2)上有两个极值点.




 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案