
科目:czsx 来源:2016年初中毕业升学考试(云南曲靖卷)数学(解析版) 题型:填空题
等腰三角形ABC在平面直角坐标系中的位置如图所示,已知点A(﹣6,0),点B在原点,CA=CB=5,把等腰三角形ABC沿x轴正半轴作无滑动顺时针翻转,第一次翻转到位置①,第二次翻转到位置②…依此规律,第15次翻转后点C的横坐标是 .

科目:czsx 来源:2016-2017学年黑龙江铁力市九年级上阶段检测数学试卷(解析版) 题型:填空题
等腰三角形ABC在平面直角坐标系中的位置如图所示,已知点A(﹣6,0),点B在原点,CA=CB=5,把等腰三角形ABC沿x轴正半轴作无滑动顺时针翻转,第一次翻转到位置①,第二次翻转到位置②…依此规律,第15次翻转后点C的横坐标是 .

科目:czsx 来源:湖北省期中题 题型:探究题
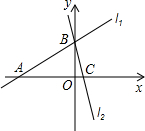
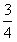 x+3 , l2:y=-3x+3,若l2上的一点M到l1的距离是
x+3 , l2:y=-3x+3,若l2上的一点M到l1的距离是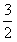 ,求点M的坐标。
,求点M的坐标。 
科目:czsx 来源: 题型:

科目:czsx 来源: 题型:
| 3 |
| 4 |
| 3 |
| 2 |
科目:czsx 来源: 题型:
| ||
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
科目:czsx 来源: 题型:解答题
 x+3,l2:y=-3x+3,若l2上的一点M到l1的距离是
x+3,l2:y=-3x+3,若l2上的一点M到l1的距离是 .求点M的坐标.
.求点M的坐标.
科目:czsx 来源:2009-2010学年江苏省泰州市姜堰市九年级(上)期中数学试卷A(解析版) 题型:解答题

 x+3,l2:y=-3x+3,若l2上的一点M到l1的距离是
x+3,l2:y=-3x+3,若l2上的一点M到l1的距离是 .求点M的坐标.
.求点M的坐标.
科目:czsx 来源:2009-2010学年江苏省泰州市兴化市文正学校九年级(上)期中数学试卷(解析版) 题型:解答题

 x+3,l2:y=-3x+3,若l2上的一点M到l1的距离是
x+3,l2:y=-3x+3,若l2上的一点M到l1的距离是 .求点M的坐标.
.求点M的坐标.
科目:czsx 来源:2009-2010学年江苏省泰州市姜堰市张甸区九年级(上)期中数学试卷(解析版) 题型:解答题
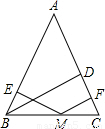
 x+3,l2:y=-3x+3,若l2上的一点M到l1的距离是
x+3,l2:y=-3x+3,若l2上的一点M到l1的距离是 .求点M的坐标.
.求点M的坐标.
科目:czsx 来源:2011-2012学年江苏省连云港市东海县平明镇中学九年级(下)第一次段考数学试卷(解析版) 题型:解答题
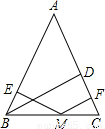
 x+3,l2:y=-3x+3,若l2上的一点M到l1的距离是
x+3,l2:y=-3x+3,若l2上的一点M到l1的距离是 .求点M的坐标.
.求点M的坐标.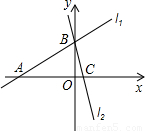
科目:czsx 来源:2012年江苏省南京市学大教育专修学校中考数学模拟试卷(5月份)(解析版) 题型:解答题
 x+3,l2:y=-3x+3,若l2上的一点M到l1的距离是
x+3,l2:y=-3x+3,若l2上的一点M到l1的距离是 .求点M的坐标.
.求点M的坐标.
科目:czsx 来源:2009年江苏省初中毕业升学模拟试卷(1)(解析版) 题型:解答题

 x+3,l2:y=-3x+3,若l2上的一点M到l1的距离是
x+3,l2:y=-3x+3,若l2上的一点M到l1的距离是 .求点M的坐标.
.求点M的坐标.
科目:czsx 来源:2009年江苏省初中毕业升学模拟(解析版) 题型:解答题

 x+3,l2:y=-3x+3,若l2上的一点M到l1的距离是
x+3,l2:y=-3x+3,若l2上的一点M到l1的距离是 .求点M的坐标.
.求点M的坐标.
科目:czsx 来源:不详 题型:解答题

| 3 |
| 4 |
| 3 |
| 2 |

科目:czsx 来源: 题型:解答题
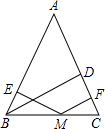
 △ABC在平面直角坐标系中的位置如图所示,点O为坐标原点.
△ABC在平面直角坐标系中的位置如图所示,点O为坐标原点.科目:czsx 来源: 题型:解答题
 △ABC在平面直角坐标系中的位置,如图所示,点A的坐标为(1,0),点C的坐标为(0,3),关于x的二次函数y=x2+bx+c的图象过点A、B、C,抛物线的对称轴与x轴交于点D.
△ABC在平面直角坐标系中的位置,如图所示,点A的坐标为(1,0),点C的坐标为(0,3),关于x的二次函数y=x2+bx+c的图象过点A、B、C,抛物线的对称轴与x轴交于点D.科目:czsx 来源: 题型:
 设点P运动的时间为t(单位:s).
设点P运动的时间为t(单位:s).科目:czsx 来源: 题型:
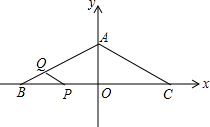 如图,在等腰三角形ABC中,AB=AC=10cm,∠ABC=30°,以BC所在直线为x轴,以BC边上的高所在的直线为y轴建立平面直角坐标系.
如图,在等腰三角形ABC中,AB=AC=10cm,∠ABC=30°,以BC所在直线为x轴,以BC边上的高所在的直线为y轴建立平面直角坐标系.