如图,△abc和△cde都是等边三角形,且点a,c,e在一条直线上.答案解析

科目：czsx 来源： 题型：解答题

17．如图，△ABC和△CDE都是等边三角形，点A、E、D在同一条直线上，且∠EBD=62°，求∠AEB的度数．

科目：czsx 来源： 题型：044

科目：czsx 来源： 题型：

如图，△ABC和△CDE都是等边三角形，且点A、C、E在一条直线上．AD与BE相等吗？证明你的结论．

科目：czsx 来源： 题型：

如图，△ABC和△CDE都是等边三角形，且点A，C，E在一条直线上．
（1）AD与BE相等吗？为什么？
（2）连接MN，试说明△MNC为等边三角形．

科目：czsx 来源： 题型：解答题

10．如图，△ABC和△CDE都是等边三角形，且点B、C、D在同一条直线上，BE交AC于F，AD交CE于H，连接FH．
（1）求证：△ACD≌△BCE；
（2）求证：AH=BF；
（3）求证：△CFH为等边三角形．

科目：czsx 来源： 题型：阅读理解

阅读材料：
如图1，△ABC和△CDE都是等边三角形，且点A、C、E在一条直线上，可以证明△ACD≌△BCE，则AD=BE．

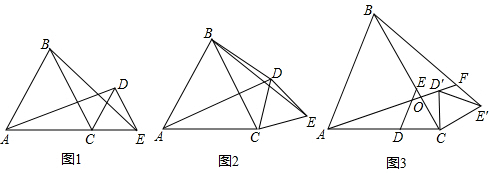
解决问题：
（1）将图1中的△CDE绕点C旋转到图2，猜想此时线段AD与BE的数量关系，并证明你的结论．
（2）如图2，连接BD，若AC=2cm，CE=1cm，现将△CDE绕点C继续旋转，则在旋转过程中，△BDE的面积是否存在最大值？如果存在，直接写出这个最大值；如果不存在，请说明理由．
（3）如图3，在△ABC中，点D在AC上，点E在BC上，且DE∥AB，将△DCE绕点C按顺时针方向旋转得到三角形CD′E′（使∠ACD′＜180°），连接BE′，AD′，设AD′分别交BC、BE′于O、F，若△ABC满足∠ACB=60°，BC=

3

，AC=

2

，
①求

BE′

AD′

的值及∠BFA的度数；
②若D为AC的中点，求△AOC面积的最大值．

科目：czsx 来源： 题型：

【观察发现】如图1，△ABC和△CDE都是等边三角形，且点B、C、E在一条直线上，连接BD和AE，BD、AE相交于点P，猜想线段BD与AE的数量关系，以及BD与AE相交构成的锐角的度数．（只要求写出结论，不必说出理由）
【深入探究】如图2，将△CDE绕点C逆时针旋转一定的角度，其他条件与【观察发现】中的条件相同，【观察发现】中的结论是否还成立？请说明理由
【拓展应用】如图3，四边形ABCD中，AB=BC，∠ABC=60°，∠ADC=30°，AD=6，BD=10，求边CD的长度．

科目：czsx 来源： 题型：解答题

11．探索研究：已知：△ABC和△CDE都是等边三角形．
（1）如图1，若点A、C、E在一条直线上时，我们可以得到结论：线段AD与BE的数量关系为：相等，
线段AD与BE所成的锐角度数为60°；
（2）如图2，当点A、C、E不在一条直线上时，请证明（1）中的结论仍然成立；
灵活运用：
如图3，某广场是一个四边形区域ABCD，现测得：AB=60m，BC=80m，且∠ABC=30°，∠DAC=∠DCA=60°，试求水池两旁B、D两点之间的距离．