如图在三角形abc中.ab=6 ac=4 bd平分角abc答案解析
科目:czsx
来源:
题型:
如图所示,在△ABC中,AB=AC,BD,CE是角平分线,图中的等腰三角形共有( )
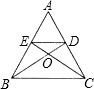
查看答案和解析>>
科目:czsx
来源:
题型:

如图所示,在△ABC中,AB=AC,∠A=36°,角平分线BD与CE相交于点O,那么图中等腰三角形共有( )
查看答案和解析>>
科目:czsx
来源:
题型:单选题
如图所示,在△ABC中,AB=AC,BD,CE是角平分线,图中的等腰三角形共有 
- A.
6个
- B.
5个
- C.
4个
- D.
3个
查看答案和解析>>
科目:czsx
来源:
题型:单选题
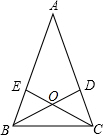 如图所示,在△ABC中,AB=AC,∠A=36°,角平分线BD与CE相交于点O,那么图中等腰三角形共有
如图所示,在△ABC中,AB=AC,∠A=36°,角平分线BD与CE相交于点O,那么图中等腰三角形共有
- A.
5个
- B.
6个
- C.
7个
- D.
8个
查看答案和解析>>
科目:czsx
来源:
题型:解答题
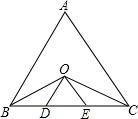 如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
(1)求证:△ODE是等边三角形.
(2)线段BD、DE、EC 三者有什么数量关系?写出你的判断过程.
(3)数学学习不但要能解决问题,还要善于提出问题.结合本题,在现有的图形上,请提出两个与“直角三角形”有关的问题.(只要提出问题,不需要解答)
查看答案和解析>>
科目:czsx
来源:期中题
题型:填空题
如图在△ABC中,AB=AC, ∠A=36°,BD平分∠ABC交 AC于点D,则图中共有( )个等腰三角形
查看答案和解析>>
科目:czsx
来源:
题型:

如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
(1)求证:△DOE是等边三角形;
(2)线段BD,DE,EC三者存什么数量关系?写出你的判断过程;
(3)数学学习不仅要能解决问题,还要善于提出问题,结合本题,在现有图形上,请提出两个与“直角三角形”有关的问题.(只要提出问题,不要解答)
(1)证明:
(2)我的判断是:
证明如下:
(3)我提出的问题是:
①
②
.
查看答案和解析>>
科目:czsx
来源:
题型:
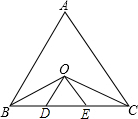
如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
(1)求证:△ODE是等边三角形.
(2)线段BD、DE、EC 三者有什么数量关系?写出你的判断过程.
(3)数学学习不但要能解决问题,还要善于提出问题.结合本题,在现有的图形上,请提出两个与“直角三角形”有关的问题.(只要提出问题,不需要解答)
查看答案和解析>>
科目:czsx
来源:
题型:
如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
(1)求证:△ODE是等边三角形.
 (2)线段BD、DE、EC 三者有什么数量关系?写出你的判断过程.
(2)线段BD、DE、EC 三者有什么数量关系?写出你的判断过程.

查看答案和解析>>
科目:czsx
来源:
题型:
如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
(1)求证:△ODE是等边三角形.
 (2)线段BD、DE、EC 三者有什么数量关系?写出你的判断过程.
(2)线段BD、DE、EC 三者有什么数量关系?写出你的判断过程.

查看答案和解析>>
科目:czsx
来源:
题型:
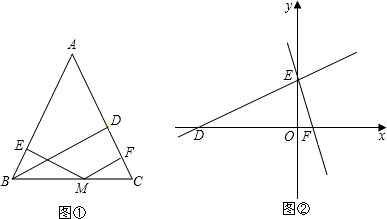
探索勾股定理时,我们发现“用不同的方式表示同一图形的面积”可以解决线段和(或差)的有关问题,这种方法称为面积法.请你运用面积法求解下列问题:在等腰三角形ABC中,AB=AC,BD为腰AC上的高.
(1)若BD=h,M是直线BC上的任意一点,M到AB、AC的距离分别为h
1,h
2.
A、若M在线段BC上,请你结合图形①证明:h
1+h
2=h;
B、当点M在BC的延长线上时,h
1,h
2,h之间的关系为
.(请直接写出结论,不必证明)
(2)如图②,在平面直角坐标系中有两条直线l
1:y=
x+6;l
2:y=-3x+6.若l
2上的一点M到l
1的距离是3,请你利用以上结论求解点M的坐标.
查看答案和解析>>
科目:czsx
来源:
题型:解答题
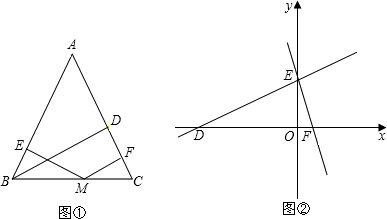
探索勾股定理时,我们发现“用不同的方式表示同一图形的面积”可以解决线段和(或差)的有关问题,这种方法称为面积法.请你运用面积法求解下列问题:在等腰三角形ABC中,AB=AC,BD为腰AC上的高.
(1)若BD=h,M是直线BC上的任意一点,M到AB、AC的距离分别为h1,h2.
A、若M在线段BC上,请你结合图形①证明:h1+h2=h;
B、当点M在BC的延长线上时,h1,h2,h之间的关系为______.(请直接写出结论,不必证明)
(2)如图②,在平面直角坐标系中有两条直线l1:y= x+6;l2:y=-3x+6.若l2上的一点M到l1的距离是3,请你利用以上结论求解点M的坐标.
x+6;l2:y=-3x+6.若l2上的一点M到l1的距离是3,请你利用以上结论求解点M的坐标.
查看答案和解析>>
科目:czsx
来源:2012年河南省中考数学模拟试卷(四)(解析版)
题型:解答题
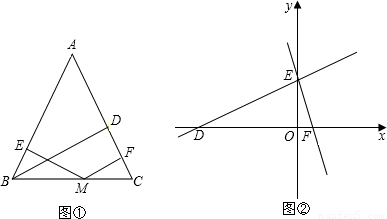
探索勾股定理时,我们发现“用不同的方式表示同一图形的面积”可以解决线段和(或差)的有关问题,这种方法称为面积法.请你运用面积法求解下列问题:在等腰三角形ABC中,AB=AC,BD为腰AC上的高.
(1)若BD=h,M是直线BC上的任意一点,M到AB、AC的距离分别为h
1,h
2.
A、若M在线段BC上,请你结合图形①证明:h
1+h
2=h;
B、当点M在BC的延长线上时,h
1,h
2,h之间的关系为______.(请直接写出结论,不必证明)
(2)如图②,在平面直角坐标系中有两条直线l
1:y=

x+6;l
2:y=-3x+6.若l
2上的一点M到l
1的距离是3,请你利用以上结论求解点M的坐标.
查看答案和解析>>
科目:czsx
来源:2011年浙江省杭州市瓜沥镇初级中学中考数学模拟试卷(解析版)
题型:解答题
探索勾股定理时,我们发现“用不同的方式表示同一图形的面积”可以解决线段和(或差)的有关问题,这种方法称为面积法.请你运用面积法求解下列问题:在等腰三角形ABC中,AB=AC,BD为腰AC上的高.
(1)若BD=h,M是直线BC上的任意一点,M到AB、AC的距离分别为h
1,h
2.
A、若M在线段BC上,请你结合图形①证明:h
1+h
2=h;
B、当点M在BC的延长线上时,h
1,h
2,h之间的关系为______.(请直接写出结论,不必证明)
(2)如图②,在平面直角坐标系中有两条直线l
1:y=

x+6;l
2:y=-3x+6.若l
2上的一点M到l
1的距离是3,请你利用以上结论求解点M的坐标.

查看答案和解析>>
科目:czsx
来源:2011年江苏省盐城市阜宁县GSJY中考数学模拟试卷(解析版)
题型:解答题
探索勾股定理时,我们发现“用不同的方式表示同一图形的面积”可以解决线段和(或差)的有关问题,这种方法称为面积法.请你运用面积法求解下列问题:在等腰三角形ABC中,AB=AC,BD为腰AC上的高.
(1)若BD=h,M是直线BC上的任意一点,M到AB、AC的距离分别为h
1,h
2.
A、若M在线段BC上,请你结合图形①证明:h
1+h
2=h;
B、当点M在BC的延长线上时,h
1,h
2,h之间的关系为______.(请直接写出结论,不必证明)
(2)如图②,在平面直角坐标系中有两条直线l
1:y=

x+6;l
2:y=-3x+6.若l
2上的一点M到l
1的距离是3,请你利用以上结论求解点M的坐标.

查看答案和解析>>
科目:czsx
来源:2011年浙江省杭州市中考数学模拟试卷(19)(解析版)
题型:解答题
探索勾股定理时,我们发现“用不同的方式表示同一图形的面积”可以解决线段和(或差)的有关问题,这种方法称为面积法.请你运用面积法求解下列问题:在等腰三角形ABC中,AB=AC,BD为腰AC上的高.
(1)若BD=h,M是直线BC上的任意一点,M到AB、AC的距离分别为h
1,h
2.
A、若M在线段BC上,请你结合图形①证明:h
1+h
2=h;
B、当点M在BC的延长线上时,h
1,h
2,h之间的关系为______.(请直接写出结论,不必证明)
(2)如图②,在平面直角坐标系中有两条直线l
1:y=

x+6;l
2:y=-3x+6.若l
2上的一点M到l
1的距离是3,请你利用以上结论求解点M的坐标.

查看答案和解析>>
科目:czsx
来源:
题型:解答题
12.(1)已知:在△ABC中,AB=AC,BD平分∠ABC,CD平分∠ACB,过点D作EF∥BC,分别交AB、AC于E、F两点(如图1).
图中共有5个等腰三角形,分别是△ABC,△AEF,△DEB,△DFC,△BDC;EF与BE、CF之间的关系是EF=BE+CF.
(2)若将(1)中“△ABC,AB=AC”改为“若△ABC为不等边三角形”,其余条件不变(如图2),则图中共有2个等腰三角形,分别是△BDE,△CFD;EF与BE,CF之间的关系是EF=BE+CF.
(3)已知:如图3,D在△ABC外,AB>AC,且BD平分∠ABC的外角∠ACG,过D点作DE∥BC,分别交AB、AC于E、F两点,则EF与BE、CF之间有何关系?写出你的结论,并加以证明
(4)已知:如图4,点D在△ABC外,BD,CD分别平分△ABC的外角∠GBC和∠HCB,过点D作DE∥BC,分别交BG,CH于E,F两点,则EF与BE,CF之间存在怎样的关系?写出你的结论,并加以证明.

查看答案和解析>>
科目:czsx
来源:
题型:
如图(1),△ABC中,AB=AC,∠B=2∠A.
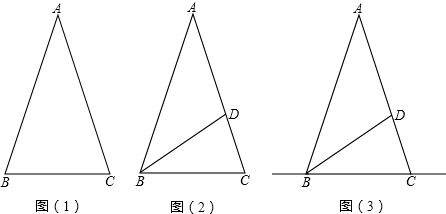
(1)求∠A和∠B的度数;
(2)如图(2),BD是△ABC中∠ABC的平分线:
①写出图中与BD相等的线段,并说明理由;
②直线BC上是否存在其它的点P,使△BDP为等腰三角形,如果存在,请在图(3)中画出满足条件的所有的点P,并直接写出相应的∠BDP的度数;如果不存在,请说明理由.
查看答案和解析>>
科目:czsx
来源:
题型:
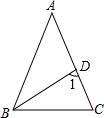
如图,在△ABC中AB=AC,∠A=36°,BD平分∠ABC,则∠1=
度,图中有
个等腰三角形.
查看答案和解析>>
科目:czsx
来源:数学教研室
题型:013
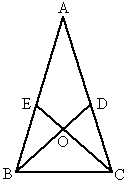
如图所示,在△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠ACB的角平分线且交于点O,则图中等腰三角形的个数为
[ ]
查看答案和解析>>

 如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC. 如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC. 如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC. (2)线段BD、DE、EC 三者有什么数量关系?写出你的判断过程.
(2)线段BD、DE、EC 三者有什么数量关系?写出你的判断过程.
 (2)线段BD、DE、EC 三者有什么数量关系?写出你的判断过程.
(2)线段BD、DE、EC 三者有什么数量关系?写出你的判断过程.

 x+6;l2:y=-3x+6.若l2上的一点M到l1的距离是3,请你利用以上结论求解点M的坐标.
x+6;l2:y=-3x+6.若l2上的一点M到l1的距离是3,请你利用以上结论求解点M的坐标.
 x+6;l2:y=-3x+6.若l2上的一点M到l1的距离是3,请你利用以上结论求解点M的坐标.
x+6;l2:y=-3x+6.若l2上的一点M到l1的距离是3,请你利用以上结论求解点M的坐标.
 x+6;l2:y=-3x+6.若l2上的一点M到l1的距离是3,请你利用以上结论求解点M的坐标.
x+6;l2:y=-3x+6.若l2上的一点M到l1的距离是3,请你利用以上结论求解点M的坐标.
 x+6;l2:y=-3x+6.若l2上的一点M到l1的距离是3,请你利用以上结论求解点M的坐标.
x+6;l2:y=-3x+6.若l2上的一点M到l1的距离是3,请你利用以上结论求解点M的坐标.
 x+6;l2:y=-3x+6.若l2上的一点M到l1的距离是3,请你利用以上结论求解点M的坐标.
x+6;l2:y=-3x+6.若l2上的一点M到l1的距离是3,请你利用以上结论求解点M的坐标.


